Определение передаточной функции исходной САУ, расчет корней характеристического уравнения

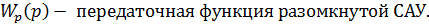
Так как обратная связь единична, то , значит

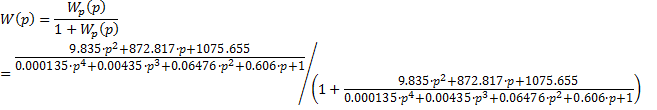
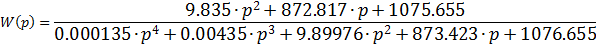
Знаменатель передаточной функции - это характеристический полином системы:

Корни этого полинома определяют вид и параметры переходной характеристики САУ. Решая уравнение в среде MathCAD,получаем корни:

Таким образом, по корням характеристического уравнения мы можем предположить, что система не устойчива. Т.к. вещественная часть (α=25,656) является положительной, то колебания будут расходящимися, таким образом система является неустойчивой. С частотой ω = 277.23 рад/с

Декремент расхождения определяется формулой . Если 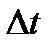взять равным периоду, то формула перепишется .

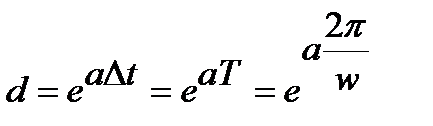Тогда ; Период колебаний ;

Коэффициент расхождения .

4.Расчет и построение частотных характеристик эквивалентной разомкнутой САУ: АФЧХ, ЛАЧХ, ЛФЧХ

b 06QxDEyqcY+UlTnJGJUbHQiH+pCsWp49qW1zRF3BjnON9xA3vYUflAw40xX133cMBCXqvUFvbovZ LF6CFMzmN1MM4DpTX2eY4QhV0UDJuN2E8eLsHMiuxy8VSQ1j79HPViato9cjqxN9nNtkwemOxYtx HaeqX3+C9U8AAAD//wMAUEsDBBQABgAIAAAAIQAuR49W3QAAAAkBAAAPAAAAZHJzL2Rvd25yZXYu eG1sTI9NT8MwDIbvSPyHyEjcWEKZYJSmE4wiLhzGgLuXmLYiH1WTbR2/HnOCm1/50evH1XLyTuxp TH0MGi5nCgQFE20fWg3vb08XCxApY7DoYiANR0qwrE9PKixtPIRX2m9yK7gkpBI1dDkPpZTJdOQx zeJAgXefcfSYOY6ttCMeuNw7WSh1LT32gS90ONCqI/O12XkNa8TH9fezMQ/N8WXe0Oqjoei0Pj+b 7u9AZJryHwy/+qwONTtt4y7YJBznQhWMari6nYNgoFALHrYabgoFsq7k/w/qHwAAAP//AwBQSwEC LQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNd LnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8u cmVsc1BLAQItABQABgAIAAAAIQCTftniKQIAAFEEAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJv RG9jLnhtbFBLAQItABQABgAIAAAAIQAuR49W3QAAAAkBAAAPAAAAAAAAAAAAAAAAAIMEAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAjQUAAAAA " strokecolor="white">

30,733

g

y

z

Рис.3. Структурная схема разомкнутой САУ

Разомкнутая САУ (рис.3) – система, не способная контролировать состояние объекта управления, т.е. это САУ без обратной связи. Передаточная функция разомкнутой САУ выглядит следующим образом:

Комплексно-частотная функция имеет вид:

Введём подстановку:

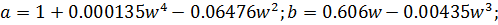
и преобразуем полученное выражение:

Тогда АЧХ и ФЧХ:

;

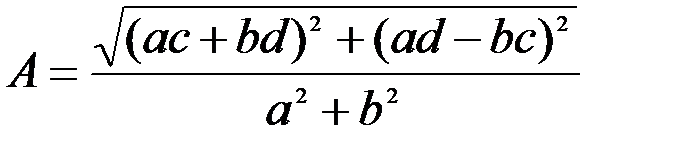Найдём значения

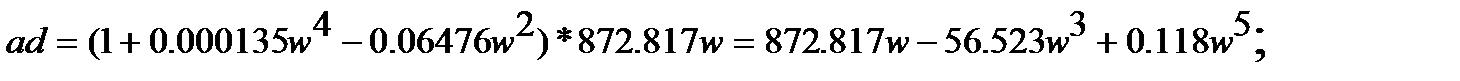
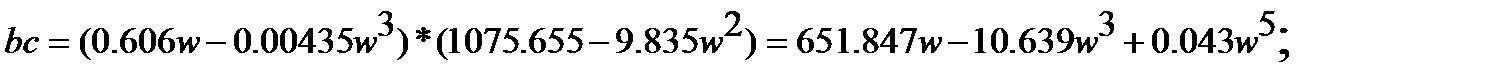
Построим с помощью пакета MatLab логарифмические амплитудную частотную характеристику (ЛАЧХ), фазово-частотную характеристику (ЛФЧХ) и амплитудную фазово-частотную характеристику (АФЧХ) для разомкнутой системы. Структурная схема разомкнутой САУ в среде MatLab представлена на рис.4.

Рис.4. Схема разомкнутой САУ в MatLab

Результаты построений представлены на рис.5, рис.6.

Рис.5. Графики ЛАЧХ и ЛФЧХ разомкнутой САУ

Рис.6. График АФЧХ разомкнутой САУ

Дата добавления: 2015-08-21