Критерий Рауса.

Критерий заключается в специальном алгоритме из коэффициентов характеристического уравнения и составлении таблицы:

Рисунок 17. Таблица Рауса.

Число строк в таблице должно быть на 1 больше чем порядок характеристического уравнения.

Для устойчивости линейной САУ необходимо и достаточно чтобы коэффициенты 1-го столбца таблицы Рауса были >0.

Запишем характеристическое уравнение из передаточной функции замкнутой системы:

Значение параметра Т=0,1 возьмем из полученной в пункте 3 области устойчивости:

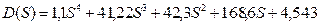
Выпишем коэффициенты:

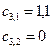
Заполним таблицу Рауса:

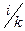
		4,543	42,3	1,1
		168,6	41,22
0,03		41,0634	1,1
4,11		36,7
1,12		1,1

Из таблицы Рауса видно, что первый ее столбец содержит только положительные коэффициенты, значит система при параметре Т=0,1 устойчива.

Дата добавления: 2015-09-03