Критерий Михайлова.

Формулировка: система устойчива, если годограф D(jω), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n – порядок системы.

Запишем систему уравнений:

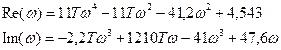
Порядок системы равен 4, значит, годограф должен последовательно пройти 4 квадранта.

Значение параметра Т=0,1 возьмем из полученной в пункте 3 области устойчивости. Построим годограф Михайлова:

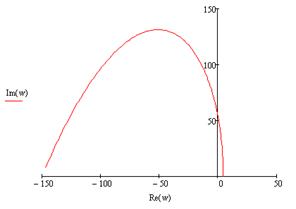
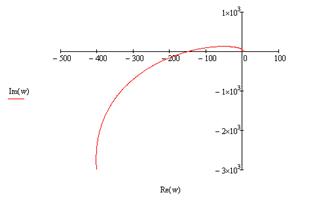
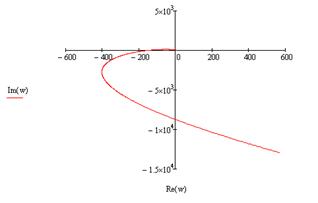
Рисунок 15. Годограф Михайлова.

Как видно из рисунка 16, годограф Михайлова начинается на действительной положительной полуоси, огибает против часовой стрелки начало координат и проходит последовательно 4 квадранта. Из этого мы можем сделать вывод о том, что область, в которой находится параметр Т=0,1, устойчива.
Исходя из рисунка 12,система будет устойчивой в 1 квадранте.

Дата добавления: 2015-09-03