Критерий Гурвица.

Это алгебраический критерий, по которому условия устойчивости сводятся к выполнению ряда неравенств, связывающих коэффициенты уравнения системы. Для этого составляется матрица из коэффициентов характеристического уравнения. Условие устойчивости заключается в требовании положительности определителя Гурвица и его диагональных миноров.

Запишем характеристическое уравнение из передаточной функции замкнутой системы:

Значение параметра Т=0,1 возьмем из полученной в пункте 3 области устойчивости и подставим в уравнение:

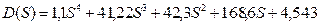
Выпишем коэффициенты, в соответствие с порядком переменной S:

Составим из коэффициентов матрицу и найдем главный определитель, а так же определители всех ее диагональных миноров:

Рисунок 16. Критерий Гурвица.

Как видно из рисунка 16 главный определитель Гурвица и его диагональные миноры >0, а значит система при параметре Т=0,1 устойчива.

Дата добавления: 2015-09-03