Тема 5. Ряды динамики

Все природные и общественные явления и процессы, изучаемые географией, рассматриваются в развитии. Такое изучение достигается путем построения и анализа рядов динамики. Ряд динамики - это последовательность упорядоченных во времени количественных характеристик развития изучаемого явления или процесса. Анализ рядов динамики позволяет выявить особенности в развитии явлений, установить тенденцию и закономерность развития, прогнозировать развитие.

В зависимости от времени представленных данных ряд динамики может быть:

- периодическим (интервальным) - ряд, каждое значение (уровень) которых относится к определенному периоду (интервалу) времени. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, годовое количество осадков и т.п.

- моментным - ряд, уровни которого приводятся на момент времени (например, на начало года, квартала, месяца). Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания. Например, если сложить величины численности населения на начало каждого месяца года, то полученная сумма не означает численность населения за год.

Основным правилом при построении рядов динамики является обеспечение сопоставимости самих рядов и их показателей. Эта сопоставимость должна быть обеспечена по ряду признаков: по содержанию объекта исследования, представляемого рядом; по полноте учета и охвату территорий; по времени и по методологии исчисления уровней ряда.

Основные показатели, используемые при анализе рядов динамики. На основе уровней ряда динамики исчисляются средний уровень ряда, показатели абсолютного и относительного роста, непосредственно характеризующие процесс развития.

Средний уровень ряда. В интервальном ряду динамики средний уровень определяется по формуле простой средней арифметической:

=

При моментном ряде применяется формула средней хронологической величины:

,

где y₁ и y_n — первый и последний уровни ряда.

Изменение уровней ряда определяется базисным и цепным способами.

Базисное абсолютное изменение ( ) представляет собой разность конкретного () и базисного (обычно начального) уровней ряда ():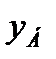

Цепное абсолютное изменение ( ) представляет собой разность конкретного () и предыдущего уровней ряда ():

По знаку абсолютного изменения делается вывод о характере развития явления: при > 0 - рост, при 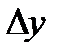< 0 - спад, при = 0 - стабильность.

Для проверки правильности расчетов применяется правило, согласно которому сумма цепных абсолютных изменений () равняется последнему базисному ():

где k = n - 1 - количество изменений уровней ряда.

Средний абсолютный прирост рассчитывается как простая средняя арифметическая величина из абсолютных приростов.

Базисное относительное изменение представляет собой соотношение конкретного и первого уровней ряда:

Цепное относительное изменение представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

Относительные изменения уровней - это по существу индексы динамики (коэффициенты роста), критериальным значением которых служит 1. Если они больше 1, наблюдается рост явления, меньше - спад, а при равенстве единице – стабильность.

Для проверки правильности расчетов применяется правило, согласно которому произведение цепных относительных изменений равняется последнему базисному.

Относительные изменения, выраженные в процентах – это темпы роста. Темпы роста показывают, сколько процентов составляет значение данного уровня от базисного или предшествующего.

Темп прироста выражает относительную величину прироста и показывает, на сколько процентов данный уровень ряда больше или меньше другого:

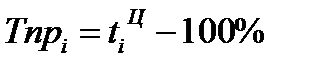
Для выявления соответствия или несоответствия абсолютных приростов и темпов развития исчисляется показатель – абсолютное значение одного процента прироста:

,

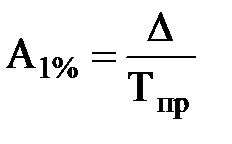Средний темп роста показывает относительную скорость изменения уровней ряда в среднем за единицу времени. При расчете среднего темпа роста используется средняя геометрическая:

.

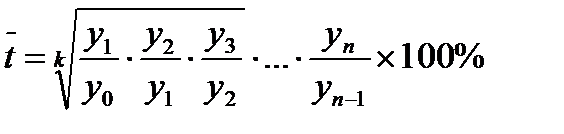Также средний темп роста можно рассчитать из последнего базисного (общего за весь период) коэффициента роста:

Обе формулы тождественны в силу взаимосвязи цепных и базисных темпов, но применяется в разных условиях: первая – когда есть все уровни, вторая – когда имеются только крайние уровни, а промежуточные данные отсутствуют.

По среднему темпу роста находится средний темп прироста: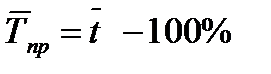

Обработка и анализ рядов динамики.

Существует несколько приемов обработки и анализа динамических рядов.

а) Сравнение и смыкание рядов. Сравнение – это прием, выявляющий различия и особенности в развитии явлений, используя несколько показателей, относящихся к различным, но связанным явлениям (например, энерговооруженность и производительность труда). Также сравнение производится по рядам одного и того же явления, относящимся к разным объектам или территориям.

В процессе сравнительного анализа динамических рядов рассчитывают коэффициент опережения и коэффициент ускорения (или замедления) среднегодовых темпов прироста.

Коэффициент опережения показывает, во сколько раз быстрее растет среднегодовой темп прироста одного ряда по сравнению с другим. Он представляет собой отношение большего среднегодового темпа прироста к меньшему за один и тот же отрезок времени:

Коэффициент ускорения показывает величину ускорения среднегодовых темпов прироста во времени и определяется соотношением среднегодовых темпов прироста за два отрезка времени:

Иногда уровни явления во времени несопоставимы вследствие их разной оценки, изменения методологии их расчета, временных или территориальных изменений, изменений единиц измерения и т.п. В таких случаях все данные следует привести в сопоставимый вид – это достигается путем смыкания рядов динамики. Вводится коэффициент сопоставимости для обоих рядов.

б) Приведение рядов к одному основанию. Этот прием широко используется при сравнительной характеристике социально-экономического развития различных территорий и стран. Суть данного приема состоит в том, что абсолютные показатели исходных (первоначальных) рядов заменяются относительными показателями, исчисленными к одной общей базе (например, к одному году). При этом за основание всех рядов может быть, в зависимости от цели аналитического исследования, принят начальный уровень ряда, средний уровень ряда, любой характерный уровень (внутри или за пределами ряда), сумма всех уровней ряда.

в) Сглаживание и выравнивание рядов. Общей задачей построения динамических рядов является обнаружение той или иной закономерности, проявляющейся в изменении явлений, отражаемых данными рядами. Иногда ряд четко обнаруживает ту или иную закономерность развития явления, но в некоторых случаях данные ряда не позволяют определить четкие тенденции развития. Можно использовать следующие методы выделения тренда (направления развития):

Укрупнение интервалов. Ряд динамики делят на некоторое достаточно большое число равных интервалов, то есть укрупняют периоды времени, к которым относятся уровни ряда динамики. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер основной тенденции развития. Если интервальные средние уровни не позволяют увидеть тенденцию, то увеличивают размах интервалов, уменьшая одновременно их число.

Метод скользящих средних. Алгоритм сглаживания методом скользящей средней может быть представлен следующим образом:

1. Определение длины интервала сглаживания, включающего в себя несколько последовательных уровней. Лучше выбрать нечетное количество уровней (например, три или пять).

2. Весь период наблюдений разбивают на участки, при этом интервал сглаживания как бы скользит по ряду шагом, равным 1.

3. Рассчитывают средние арифметические из уровней ряда, образующих каждый участок. Результат записываем в середине интервала.

При этом формулы для расчета скользящей средней следующие:

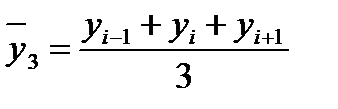- трехуровневое выравнивание

- пятиуровневое выравнивание

4. Фактические значения ряда, стоящие в середине каждого участка, заменяют на соответствующие средние значения.

Недостаток метода скользящей средней заключается в условности определения сглаженных значений для уровней в начале и в конце ряда. При сглаживании по трем уровням условное значение первого уровня нового ряда можно рассчитать по формуле

.

Для уровня в конце нового ряда при таком сглаживании формула аналогична:

.

При сглаживании по пяти уровням условными оказываются по два уровня в начале и в конце нового ряда. Первое условное значение определяется по формуле

,

а второе – по формуле

.

Для двух уровней в конце нового ряда при таком сглаживании формулы аналогичны. Так, последнее расчетное значение определяется по формуле

,

а предпоследнее значение по формуле

.

Метод аналитического выравнивания подразумевает формализацию основной, проявляющейся во времени тенденции развития изучаемого явления. В итоге получают наиболее общий результат действия всех причинных факторов, а отклонение конкретных уровней ряда от формализованных значений объясняют действием фактов, проявляющихся случайно или циклически. При этом производится выравнивание ряда динамики по аналитической формуле, которая является уравнением прямой или кривой линии, ординаты точек которой максимально близки к значениям уровней исходного ряда динамики. В качестве примера можно взять уравнение прямой. В результате приходят к трендовой модели вида

где 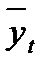– выравненные уровни ряда, и - параметры прямой, t – время, к которому относятся уровни ряда, т.е. порядковые номера периодов или моментов времени.

Для нахождения параметров а и b решается система двух уравнений:

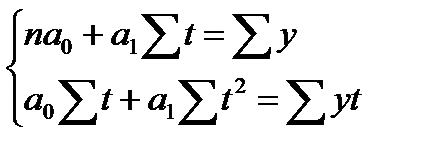
где У – фактические уровни исходного ряда, n – число уровней.

Решение уравнений значительно упрощается, если отсчет времени t вести с середины ряда: вверх со знаком «минус», вниз со знаком «плюс», так чтобы равнялась нулю. Тогда, если 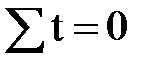, параметры оказываются равны:

, .

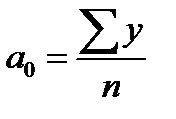Подставляя вместо t его значения, исчисляем теоретический ряд. Правильность выравнивания доказывается тем, что сумма исходных уровней равна сумме выровненных уровней .

г) Измерение сезонных колебаний. Самый простой способ определения сезонных различий в развитии изучаемого процесса или явления состоит в исчислении за каждый месяц индексов сезонности, которые определяются отношением фактических месячных уровней к среднемесячному за год. При этом для того, чтобы освободиться от влияния различных случайных несезонных колебаний, исчисление индексов сезонности следует вести не по одному, а по нескольким годам (минимум трёх лет). При расчёте индекса сезонности для каждого месяца определяется средняя величина уровня за несколько лет (), затем вычисляется среднемесячный уровень для всего ряда (). Индекс сезонности вычисляется по формуле:

Для наглядного представления сезонных колебаний на основе индексов сезонности строят график, отображающий сезонную волну. По оси абцис откладываем время (месяцы), по оси ординат –значение индекса сезонности. За начало отчёта оси ординат берём I = 100%.

д) Установление закономерностей развития явлений и процессов. Интерполяцией называется определение неизвестного уровня внутри динамического ряда, исходя из известных его уровней за предшествующий и последующий сроки. Проводится она в зависимости от типа динамики и рассматриваемых показателей по методу либо арифметической простой или взвешенной, либо хронологической, либо геометрической.

Экстраполяцией называется определение неизвестного уровня за пределами ряда (впереди или позади него), исходя из известных (последующих или предшествующих) его уровней. Она основана на исчислении средних либо абсолютных приростов, либо темпов роста:

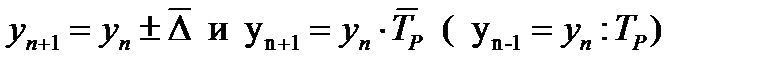
Метод прогнозирования предполагает, что та или иная закономерность развития, действовавшая в прошлом, сохранится и в прогнозируемом будущем, т.е. прогноз основан на экстраполяции (распространении) этой закономерности на будущее. Поэтому надежность и точность прогноза зависят от того, насколько близкими к действительности окажутся эти предположения и насколько точно удалось охарактеризовать выявленную в прошлом закономерность. При этом особое значение имеют вопросы определения длины базы и будущего периода.

Если выявление тенденции производилось путем аналитического выравнивания ряда, то для прогнозирования методом экстраполяции используется уравнение тренда, в которое подставляют значения в будущие годы.

Дата добавления: 2015-10-30