Тема 7. Статистические приемы изучения связей между явлениями

Исследование объективно существующих зависимостей и взаимосвязей между явлениями и процессами позволяет глубже понять сложный механизм причинно-следственных отношений между явлениями. В статистике для исследования интенсивности и вида причинных связей широко применяется корреляционный и регрессионный анализ. Выявление количественных соотношений дает возможность лучше понять природу исследуемого явления.

Различают два вида зависимости между экономическими явлениями: функциональная и стохастическая (статистическая). Зависимость между двумя величинами х и у называется функциональной, если каждому значению величины х соответствует единственное значение величины у, и наоборот. Примером функциональной связи в экономике может служить зависимость производительности труда от объема произведенной продукции и затрат рабочего времени.

Чаще встречается статистическая зависимость, когда каждому фиксированному значению независимой переменой х соответствует не одно, а множество значений зависимой переменной у, причем заранее нельзя сказать, какое именно значение примет у. Это связано с тем, что на значение у кроме переменной х влияют и другие случайные факторы.

Для изучения связей применяются балансовый и индексный методы, метод сопоставления параллельных рядов, метод аналитических группировок, корреляционный анализ, регрессионный анализ и другие. Среди множества методов, применяемых при исследовании связей между явлениями, рассмотрим лишь несколько.

Метод сопоставления двух параллельных рядов. При этом факторы, характеризующие результативный признак, располагают в возрастающем или убывающем порядке (в зависимости от целей исследования), затем прослеживают изменение величины результативного признака. Таким образом можно установить наличие связи и её направление.

Метод аналитических группировок. Чтобы выявить зависимость с помощью этого метода, необходимо провести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее значение результативного признака. Затем сопоставляют изменения результативного признака по мере изменения факторного.

Корреляционный анализ. Установить наличие связи между исследуемыми переменными, выявить структуру этих связей и измерить их тесноту можно с помощью соответствующих корреляционных характеристик, и совокупность используемых для этих целей методов называют корреляционным анализом. Данные методы применяются для определения аналитического выражения влияния факторных признаков на результативный. При корреляционном анализе измеряют тесноту связи между варьирующими признаками и оценивают факторы, оказывающие наибольшее влияние на результативный признак. Наиболее разработанным является методика расчета парных коэффициентов корреляции.

Оценка тесноты связи между двумя признаками.

Построение корреляционной таблицы. Самым простым методом является построение корреляционной таблицы. В основу таблицы положена группировка двух изучаемых во взаимосвязи признаков – х и у. Частоты показывают количество соответствующих сочетаний х и у. Если они расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. Если они концентрируются около одной из диагоналей, имеет место прямая или обратная связь. В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения – одно по х, другое по у.

Корреляционная таблица

Уровни признака х	Уровни признака у
у1	у2	…	ym	Итого	у
х1	f11	f12	…	f1m		y1
х2	f21	f22	…	f2m		y2
			…			…
xk	fk1	fk2	…	fkm		yk
Всего	∑fi1	∑fi2	…	∑fim
х	х1	х2	…	хm	-

Наглядным изображением корреляционной таблицы является корреляционное поле, которое графически представляет статистическую зависимость двух признаков. Корреляционное поле – это график, где на оси абсцисс откладывается значение факторного признака х, а по оси ординат — результирующего у. Точками показывается сочетание первичных наблюдений х и у. Примерами может быть зависимость между количеством внесенных минеральных удобрений (х) и урожайностью (у) в сельском хозяйстве (прямая зависимость), а в случае обратной зависимости — зависимость между объёмом выбросов загрязняющих веществ (х) и качеством атмосферного городов (у).

Метод корреляции знаков. Наиболее простым показателем, используемым для измерения тесноты зависимости при параллельном рассмотрении у n единиц значений х и у, является коэффициент Фехнера (коэффициент корреляции знаков). Он основан на сравнении поведения отклонений индивидуальных значений каждого признака от своей средней величины. При этом во внимание принимаются не величины отклонений (х_i - x) и (у_i-у), а их знаки («+» или «-»). Определив знаки отклонения от средней величины в каждом ряду, рассматривают все пары знаков и подсчитывают число их совпадений ∑C и несовпадений ∑Н. Коэффициент Фехнера (К_ф) рассчитывается как отношение разности чисел пар совпадений и несовпадений знаков к их сумме, т.е. к общему числу наблюдаемых единиц:

Очевидно, что если знаки всех отклонений по каждому признаку совпадают, то ∑Н = 0 и тогда К_ф = 1. Это характеризует наличие прямой связи. Если все знаки не совпадают, то ∑С = 0, а К_ф = -1, что характеризует обратную связь. Коэффициент Фехнера, как и любой другой показатель тесноты связи, может принимать значения от -1 до +1. Однако равенство коэффициента Фехнера единице нельзя оценивать как свидетельство функциональной зависимости между х и у. Поскольку К_ф зависит только от знаков и не учитывает величину самих отклонений х и у от их средних величин, то он практически характеризует не столько тесноту связи, сколько её наличие и направление.

Корреляционный анализ количественных признаков. Одним из наиболее часто применяемых показателей взаимозависимости двух случайных величин является парный коэффициент корреляции. Он является мерой линейной статистической зависимости между двумя величинами.

Парный коэффициент корреляции, характеризующий тесноту связи между случайными величинами х и у, определяется по формуле:

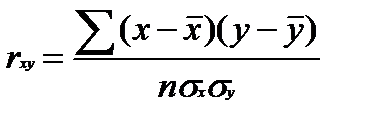
Парный коэффициент корреляции изменяется в пределах от -1 до +1, т.е. - 1 < r < +1, причем если r равняется +1 или - 1, то между величинами х и у связь функциональная, прямая при r = +1 и обратная при r = - 1. Если же r = 0, то между величинами х и у линейная связь отсутствует и они называются некоррелированными.

Качественная характеристика связи

Значение r	Характер связи
от 0 до |± 0,3|	практически отсутствует
от |± 0,31| до |± 0,5|	слабая
от |±0,5| до |±0,7|	умеренная
от |± 0,7| до |± 1|	сильная

Значения рассматриваются по модулю, так как степень тесноты связи зависит от близости r к единице без учета знака.

Корреляционный анализ порядковых переменных: ранговая корреляция. Порядковая переменная позволяет упорядочивать статистически исследованные объекты по степени появления в них анализируемого свойства. К порядковым переменным обращаются в ситуациях, когда количественно измерить степень проявления этого свойства невозможно или когда измерения рассматриваются как вспомогательное средство для последующего ранжирования рассматриваемых объектов. Ранговый коэффициент корреляции характеризует степень статистической связи между порядковыми переменными.

Ранжирование - расположение объектов в порядке убывания степени проявления в них изучаемого свойства. В случаях неразличимости рангов используют объединенные (или связные) ранги. Всем связным рангам присваивается один и тот же ранг, равный средней арифметической рангов, входящих в данную группу. Например, если в ранжировании объекты, находящиеся на 3-м, 4-м, 5-м и 6-м местах, неразличимы поданному признаку, то каждому из них присваивается ранг, равный 4,5. Таким образом, при применении ранговой корреляции коррелируются не сами значения показателей х и у, а их ранги.

Ранговый коэффициент корреляции Спирмена (ρ - «ро») рассчитывается по формуле

где d = N_x- N_y, т.е. разность рангов каждой пары значений х и у, a n - число наблюдений.

Коэффициент корреляции рангов Кендэла (τ - «тау») определяется по формуле:

Порядок расчета τ следующий.

1. Значения х и у ранжируются, т.е. определяются N_x и N_y.

2. Значения N_x записываются строго в порядке возрастания (или, наоборот, убывания): 1, 2,..., n.

3. Ранги второго показателя (N_y) располагаются в порядке, соответствующем значению х в исходных данных.

4. Последовательно рассматривается каждая пара рангов N_x и N_y (где N_x расположены строго в порядке возрастания) и подсчитывается число следующих за ними пар рангов, у которых N_y: а) более высокого порядка; б) меньше по значению. Сумма случаев «а» («правильного» следования рангов х и у) учитывается как баллы со знаком «+» и обозначается символом Р. Сумма случаев «б» (инверсий) учитывается как баллы со знаком «-» и обозначается символом Q.

5. Определяется общая сумма баллов, которая обозначается символом S, т.e. S=P+Q.

6. Полученная сумма (S) сопоставляется с максимальной, которая равна в случае, если в обоих рядах ранги следуют строго последовательно от 1 до n.

Дата добавления: 2015-10-30