Основные обозначения и правила построения индексов.

Признак, по которому прослеживается изменение и строится индекс, называется индексируемым. Его символ пишется у основания индекса.

При индексировании применяются количественные (численность рабочих, натуральный или физический объем продукции, посевная площадь и т.п.) качественные (зарплата, выработка рабочих, цена, себестоимость, трудоемкость, рентабельность, урожайность и т.п.), суммарные (фонд зарплаты, товарооборот, затраты и др.) признаки.

Условные обозначения, используемые в теории индексного метода:

i - индивидуальный индекс

I - сводный индекс

р - цена

q - количество (товара или выпущенной продукции);

z - себестоимость продукции;

Q - стоимостной объём продукции;

w - трудоемкость единицы продукции;

Т - общие затраты времени на производство продукции или общая численность работников;

S - посевная площадь;

y - урожайность

1 - подстрочный символ показателя текущего (отчетного) периода;

0 - подстрочный символ показателя предшествующего (базисного) периода;

Индивидуальные индексы. При анализе простых явлений или сложных явлений без учёта структуры применяют индивидуальные индексы, показывающие изменение величины показателя у одной единицы совокупности. Например, такие простые явления как количество проданного товара q и его цена р своим произведением образуют такое сложное явление, как выручка от продаж Q=qp. Сравнение их значений по отдельности для конкретного товара в отчетном периоде времени относительно какого-либо базисного периода и дает индивидуальные индексы. Они строятся как простые относительные величины и состоят из одного индексируемого признака, принимая следующий вид:

индекс количества товара:

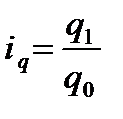
цены товара

выручки от продаж (товарооборота)

Формы общих индексов: агрегатная, средняя арифметическая, средняя гармоническая, условия их применения. Индекс становится общим, когда в основной формуле показывается неоднородность изучаемого явления. Например, анализируется изменение выручки от продаж не одного, а всех или нескольких видов товаров. Построение общих индексов отличается сложностью. Общие (сводные) индексы – это такие индексы, которые характеризуют изменение признака по совокупности единиц. Сводные индексы могут быть представлены в трёх формах:

- агрегатной;

- средней арифметической;

- средней гармонической.

Исходной формой выражения сводного индекса является агрегатная форма, которая придает объективность общим индексам. В их построение входят два признака: первый – индексируемый – тот, изменение которого оценивается и величина которого берется разная: в числителе отчетного периода, в знаменателе базисного; второй – весовой признак, выполняющий роль соизмерителя; его величина берется и в числителе и в знаменателе одинаковой, так как она не должна оказывать влияние на исследуемое изменение.

При расчете агрегатного индекса для разнородной совокупности находят такой общий показатель, в котором можно объединить все ее элементы. Например, цены различных товаров, реализуемых в розничной торговле, складывать неправомерно, однако с экономической точи зрения вполне допустимо суммировать товарооборот по этим товарам. В статистической практике определяется объем товарооборота всех продовольственных товаров, объем товарооборота всех непродовольственных товаров, а также общий объем товарооборота. Если мы сравним товарооборот по определенному кругу рассматриваемых товаров в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:

Числитель данного индекса представляет собой товарооборот текущего периода (сумма цен различных товаров, умноженных на объемы их реализации), знаменатель — товарооборот предшествующего периода.

На величину данного индекса оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких качественных показателей, как цена, себестоимость, производительность труда, количественный показатель обычно фиксируют на уровне текущего уровня. Таким способом получают сводный индекс цен:

Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает изменение цен. Изменение же количества реализованной продукции не влияет на величину индекса. Разность числителя и знаменателя будет отражать величину экономии (знак «-») или перерасхода («+») покупателей от изменения цен:

Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения:

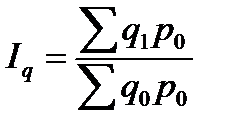
Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.

Перечисленные индексы взаимосвязаны:

Используя эту взаимосвязь, нужно проверять правильность выполненных расчетов.

Также индексный метод можно применить в анализе изменения затрат на производство и себестоимости продукции (сводный индекс затрат на производство, себестоимости, физического объёма), в анализе производительности труда (сводный индекс ПТ в стоимостном выражении по выработке, сводный индекс ПТ в стоимостном выражении по трудоемкости).

Общие индексы как средние из индивидуальных. Помимо записи общих индексов в агрегатном виде, на практике часто используют формулы их расчета как величин, средних из соответствующих индивидуальных индексов.

Используя их формулы, получаем, что q₁ = q₀i_q и p₁ = p₀i_p, а также, что q₀ =q₁/i_q и р₀=р₁/i_p. Подставив отчетные значения количества товара и цены в формулу общего индекса выручки, получим

Значит, общий индекс выручки можно определять только через ее базисные значения сумножением в числителе на индивидуальный индекс выручки по конкретному товару.

Также можно получить данный индекс через текущие (отчетные) показатели

В первом случае индекс называется среднеарифметическим, во втором – среднегармоническим по аналогии с соответствующими средними величинами. Данные виды индексов можно рассчитать для цены и количества (для качественных и количественных характеристик).

Отдельно можно рассмотреть агрегатные индексы качественных и количественных показателей.

Агрегатные индексы качественных показателей. К качественным показателям относятся цена, себестоимость, трудоёмкость, урожайность и т.д.. При вычисления агрегатных индексов по качественным показателям должно быть устранено влияние количественных показателей (в качестве весов используют количество одного из периодов). Обычно берут количество отчетного, или текущего периода.

Агрегатный общий индекс Ласпейреса для количества товаров как первого фактора выручки определяется по формуле:

Аналогично можно записать агрегатный общий индекс Ласпейреса для цен как первого фактора выручки, то есть

=

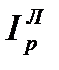В формулах Ласпейреса знаменатели по существу одинаковые, представляя собой выручку базисного периода, а числители разные. В первой формуле это отчетная выручка в базисных ценах (количество товаров отчетное, а цены - базисные), во второй формуле наоборот - базисная выручка в отчетных ценах (цены отчетные, а количество товаров - базисное).

Агрегатные общие индексы Пааше применяются ко вторым факторам. Поэтому такой индекс для цен как второго фактора выручки определяется по формуле:

=

Аналогично можно записать агрегатный общий индекс Пааше для количества товаров как второго фактора выручки, то есть

=

В формулах Пааше числители по существу одинаковые, представляя собой выручку отчетного периода, а знаменатели аналогичны числителям формул Ласпейреса.

Произведения количественного индекса Ласпейреса и ценового индекса Пааше, а также ценового индекса Ласпейреса и количественного индекса Пааше дают общий индекс выручки.

Дата добавления: 2015-10-30