|
Читайте также: |
Рассмотрим отдельно на каждом этапе затраты на хранение и затраты на закупку продукции. В общем случае на каждом этапе затраты на хранение каждой новой единицы продукции и затраты на закупку каждой новой единицы продукции зависят от объема закупаемой продукции на этом этапе. Так в предыдущем примере, затраты на закупку одной единицы продукции были равны 10 при y i ≤3, а в противном случае каждая новая единица стоила 20 денежных единиц (т.е. являлись возрастающей функцией). Затраты за хранение одной единицы продукции на этапе в этом примере были постоянными.
В рассматриваемом частном случае будем предполагать, что на каждом этапе в отдельности затраты на закупку и на хранение каждой новой единицы продукции являются либо постоянными, либо убывающими функциями от объема закупаемой партии на этапе. При этом, эти величины могут меняться от этапа к этапу различным образом. Будем также предполагать, что начальный запас x 1 = 0. Последнее ограничение не является существенным, так как, уменьшив спрос на первом этапе на величину начального запаса, можно всегда считать это условие выполненным. При сделанных предположениях будут справедливы следующие два свойства [1, c463].
1. На всех этапах выполняется равенство
.
2. Размер оптимального заказа 
может принимать только одно из следующих значений
0, b i, b i + b i+1, …, b i + …+ b n.
Отметим, что эти свойства позволяют существенно сократить объем вычислений. Приведем пример. Расчеты проводятся аналогично предыдущему случаю за исключением множеств возможных значений x i, и y i.
Пример. Рассмотрим 4 – этапную систему управления запасами. Пусть начальный запас равен 2 единицам продукции. Стоимость закупки единицы продукции составляет 4 денежных единицы для всех этапов, а стоимость хранения единицы продукции переходящей с этапа i на этап i + 1 составляет одну денежную единицу для всех этапов. Величины спроса на этапах и стоимость оформления заказов имеют следующие значения: (3; 3), (3; 2), (4; 1), (3; 4).
Чтобы свести задачу к частному случаю нужно из спроса на первом этапе вычесть начальный запас. Соответствующие значения спроса и стоимости оформления заказа по этапам будут иметь вид: (1; 3), (3; 2), (4; 1), (3; 4).
Этап 1. В соответствии со свойством 2 величина x 2 может принимать следующие значения:
0, b 2 =3, b 2 + b 3 = 3 + 4 = 7, b 2 + b 3 + b 4 = 3 + 4 + 3 = 10.
| x 2 | h 1 x 2 | y 1 | C 1(y 1) | f 1(x 2) |
Этап 2. Возможные значения величины x 3
0, b 3 = 4, b 3 + b 4 = 4 + 3 = 7,. x 3Î{0; 4; 7}.
Величина y 2 может принимать значения, совпадающие с возможными значениями x 2 y 2Î{0; 3; 5; 6}. Значения функций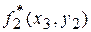 
, f 2(x 3) и соответствующие 
приведены в следующей таблице
| x 3 | h 2 x 3 | y 2=0 | y 2=3 | y 2=7 | y 2=10 | f 2(x 3) |
|
| C 2=0 | C 2=14 | C 2=30 | C 2=42 | ||||
| ¾ | ¾ | ||||||
| ¾ | ¾ | ||||||
Покажем нахождение значений функции 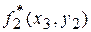(33) для двух случаев x 3 =4 и x 3=7. Рассмотрим сначала случай x 3 = 4
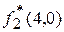= C 2(0) + 1´4 + f 1(4-0+3) = 0 + 4 + 42 = 46;
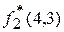= C 2(3) + 1´4 + f 1(4-3+3)
Так как данного значения x 2 = 4-3+3=4 нет в первой таблице, в соответствующей клетке для функции 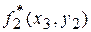стоит прочерк.
= C 2(7) + 1´4 + f 1(4-7+3) = 30 + 1´4 + 7 = 41.
Для значения y 2 = 10 получается отрицательное значение x 2, что недопустимо по условиям задачи (дефицит не допускается). Поэтому в соответствующей клетке стоит прочерк. Теперь случай x 3 = 7.
= C 2(0) + 1´7 + f 1(7-0+3) = 0 + 7 + 57;
= C 2(3) + 1´7 + f 1(7-3+3) = 14 + 7 + 42 = 63;
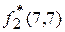= C 2(7) + 1´7 + f 1(7-7+3) = 30 + 7 + 22 = 59;
= C 2(10) + 1´7 + f 1(7-10+3) = 42 + 7 + 7 = 56.
Этап 3. Возможны только два значения величины x 4
0, b 4 = 3.
| x 4 | h 3 x 4 | y 3=0 | y 3=4 | y 3=7 | f 3(x 4) | 
|
| C 3=0 | C 3=17 | C 3=29 | ||||
| ¾ | ||||||
| ¾ |
Этап 4. Величины x 5 принимает единственное значение x 5=0.
| x 5 | h 4 x 5 | y 4=0 | y 4=3 | f 4(x 5) |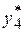 
|
| C 4=0 | C 4=16 | ||||
Итак, минимальные суммарные затраты равны 53. Теперь нужно найти величины 
. Будем находить их, двигаясь по таблицам в обратном направлении. Из последней таблицы 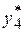=0. Тогда из соотношения (32) при i= 4 получим 
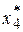=3. Из таблицы третьего этапа в строке с этим значением находим =7. Снова из соотношения (32) при i= 3 получим 
=0. В таблице второго этапа в соответствующей строке находим =3. Опять из (32) при i= 2 получим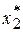 
=0. Далее, из таблицы первого этапа 
=1. Таким образом, на первом этапе нужно заказывать одну единицу продукции, на втором - три, на третьем - семь, а на четвертом заказывать не надо. При этом суммарные затраты составят 53 денежных единицы.
Дата добавления: 2015-10-23; просмотров: 92 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Однопродуктовая n - этапная динамическая модель без дефицита | | | Одноэтапная модель с мгновенным спросом при отсутствии затрат на оформление заказа |