Однопродуктовая статическая модель при непрерывном поступлении заказа без дефицита

Пусть продукция поступает на склад непрерывно с производственной линии с интенсивностью l единиц в единицу времени. Продукция отпускается со склада непрерывно с интенсивностью b единиц в единицу времени на сборочный конвейер. Поставка продукции на склад продолжается до тех пор, пока объем поставленной партии не станет равным y. После этого поставка прекращается и возобновляется в момент полного истощения запаса. Таким образом, каждая новая партия продукции начинает поступать на склад в момент, когда уровень запаса становится равным нулю. Отметим, что такое возможно только при условии l > b.

По прежнему K - затраты на оформление заказа; h - стоимость хранения единицы продукции в течение единицы времени.

Требуется определить размер заказываемой партии y так, чтобы суммарные расходы в единицу времени были минимальны.

График зависимости объема запаса от времени показан на рисунке 4. На отрезке[0, A] длиной t₁ запас увеличивается с интенсивностью равной l-b единиц продукции в единицу времени, а на отрезке [A, B] длиной t₂ запас уменьшается с интенсивностью равной b единиц продукции в единицу времени. Пополнение и расходование запаса на складе происходит циклически. Обозначим длину такого отрезка [0, B] символом t. Пусть q - максимальная величина продукции на складе. За время t₁ на склад поставляется партия продукции объемом y, следовательно, справедливо соотношение

y

q

0 A B

	Рис 4

(14)

Так как величина q полностью расходуется за интервал длительностью t₂ при интенсивности расходования равной b, а накапливается за интервал длительностью t₁ при интенсивности накопления равной l-b, то справедливы равенства:

; . (15)

Подставим (14) в (15) и приравняем правые части равенств (15)

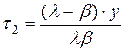(16)

Величина t определяется из условия, что за это время со склада выдается объем продукции равный y

t = y/b. (17)

Величина среднего запаса на отрезке [0, B] равна q/2. Подставляя в первую формулу (15) выражение для t₂, найдем значение q. Тогда затраты на хранение за период составят

.

Суммарные затраты на периоде будут состоять из затрат на хранение

и затрат на оформление заказа. Разделив их на длину периода (17) получим средние суммарные затраты в единицу времени

(18)

Запишем необходимые условия минимума

. (19)

Из равенства (19) легко находим оптимальный размер партии

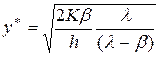. (20)

Так как вторая производная функции S (y) больше нуля всюду за исключением точки 0, то y^* (20) действительно является точкой минимума этой функции. При этом длина цикла и минимальное значение средних затрат в единицу времени задаются соотношениями

; .

Пример 3. Компания "ZZZ" продает упаковочную тару. В одном здании располагается производственный цех и склад-магазин. Максимальная мощность производственного цеха – 1000 коробок в час. Средняя величина спроса составляется 600 коробок в час. Т.к. у компании "ZZZ" нет дополнительных складских помещений, то излишне произведенные коробки хранятся прямо на территории склада магазина. Руководство фирмы оценивает свои затраты на хранении в 10 копеек в час на одну коробку. Стоимость запуска оборудования в производственном цехе оценивается в 1200 рублей. Определите оптимальный размер партии для производственного цеха, с учетом того, что фирма минимизирует свои затраты на производство и хранение. Определите величину затрат в единицу времени для выбранного объема производства и доля времени в одном цикле, которую производственный цех будет простаивать.

Решение. В соответствие с условиями задачи имеем:

K= 1200; b= 600; α=1000; h= 0.1

По формуле (20) находим оптимальный объем заказываемой магазином партии

По формуле (18) найдем средние суммарные затраты в единицу времени

;

Теперь определим t₂ по формуле (16)

Таким образом, с целью минимизации средних суммарных затрат в час необходимо производственному цеху производить 6000 коробок непрерывно. При этом величина средних суммарных затрат в час составит 120 рублей, а протяженность простоя производственного цеха между двумя рабочими циклами составит 4 часа.

Дата добавления: 2015-10-23