Nbsp; d

	Рис 5

Требуется найти объем партии y и величину максимального дефицита d, доставляющих минимум суммарным затратам в единицу времени.

Вычислим затраты на хранение запаса на интервале [0; C ]. Как и в предыдущих случаях, средний уровень запаса на этом интервале составляет q/ 2. Поэтому затраты на хранение будут равны

h (t₁ + t₂) q /2. (21)

Аналогично потери от дефицита на интервале [ C; F ] составят

p (t₃ + t₄) d /2. (22)

Величина максимального запаса q накапливается за время t₁ с интенсивностью l - b, следовательно

q = (l - b)t₁ (23)

С другой стороны этот запас расходуется с интенсивностью l за время t₂

q = b× t₂ (24)

Из соотношений (22) и (23) получаем

b× t₂ = (l - b)t₁ (25)

Из аналогичных рассуждений для величины максимального дефицита d получаем

d = b× t₃ = (l - b)t₄. (26)

За весь цикл расходуется весь объем партии, поэтому

t₁ + t₂ +t₃ + t₄ = y / b (27)

Запишем суммарные расходы за цикл

H = K + h + p (28)

Здесь первое слагаемое выражает затраты на оформление заказа, второе слагаемое - затраты за хранение продукции на складе, а третье - потери от дефицита (смотри (21), (22) соответственно). Выразим t_i i=1,…,4 из соотношений (23) - (26) через q, d, b, l подставим в равенство (28)

H = K + h 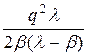+ p .

Разделим это выражение на длину цикла, полученную из соотношений для t_i i=1,…,4

t₁ + t₂ +t₃ + t₄ = , (29)

и получим выражение для средних суммарных затрат в единицу времени

S (q, d)= .

Введем новую переменную z=q + d вместо переменной d. Тогда выражение для S (q, d) примет следующий вид

S (q, z) = .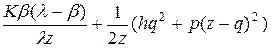

Приравняем нулю производные от этой функции по q и z:

,

.

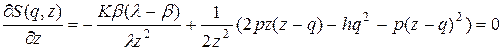Разрешая эти уравнения относительно q и z, а затем, заменяя z на q+d, получим следующие равенства для q и d

q= d=q .

Из последних равенств и соотношений (27), (29) получим оптимальные размеры заказываемой партии и максимального дефицита:

y^*= , . (30)

Пример 4. Компания K.D.M. производит одноразовую стерильную одежду для различных нужд. Производственный процесс состоит из двух этапов. На первом этапе, в цехе А, производится собственно одежда, а на втором этапе, в цехе Б, производится стерилизация одежды и ее упаковка по 1 шт. Максимальная мощность цеха А – 2000 изделий в час. В цехе Б за этот же временной интервал можно обработать только 1600 изделий. Проверка и запуск оборудования в цехе А на один производственный цикл обходится компании в 4000 рублей. Производственный процесс не предусматривает складирования изделий, в силу чего излишки, произведенные в цехе А, временно размещаются в складской зоне. Использование площади не по назначению обходится компании в 20 копеек в час на одно, хранящееся изделие. С другой стороны, в цехе Б работает ряд инженеров, контролирующих процесс и если цех Б простаивает, в силу отсутствия изделий, нуждающихся в стерилизации, то компания вынуждена фактически платить зарплату неработающим сотрудникам. Отталкиваясь от мощности цеха Б это оценивается в 30 копеек в час на одно изделие. Компания хочет минимизировать свои затраты связанные с этими двумя цехами. Определите оптимальный размер партии, которую необходимо производить в цехе А? Определите максимальный размер дефицита и максимальный запас товар на складе, а также длину интервала времени в течении которого будет работать цех А.

Решение. В соответствие с условиями задачи имеем:

K= 4000; b= 1600; α=2000; h= 0.2; p= 0,3;

По формулам (30) находим оптимальный объем партии, производимой непрерывно в цехе А и максимальный размер дефицита

Теперь определим максимальный запас товара на складе

;

Теперь определим t₁ по формуле (23)

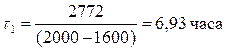
Таким образом, с целью минимизации средних суммарных затрат в час необходимо цеху А производить 23904 коробки непрерывно. При это максимальный запас товар на складе составит 2772 штуки, а максимальный дефицит – 1848 штук. Протяженность непрерывной работы цеха А – 6 часов 58 минут.

Дата добавления: 2015-10-23