Однопродуктовая статическая модель без дефицита

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

«Челябинский государственный университет»

Кафедра математических методов в экономике

Методические указания

Модели управления запасами

для студентов экономического факультета всех специальностей

Челябинск

УДК – 332.64

Методические указания «Модели управления запасами» Челябинск, ГОУВПО «ЧелГУ», 2008, 47 с.

Методические указания содержат краткую теоретическую справку по теме «Модели управления запасами», набор задач для практических занятий по соответствующему разделу дисциплины «Математика». Приводятся примеры решения задач.

Предназначены для студентов 2-3 курсов экономического факультета.

Составители: В.Е. Рольщиков, канд. физ. – мат. наук, доцент, каф. Математические методы в экономике.

П.С. Кабанов, преподаватель каф. Математические методы в экономике.

О.С. Лямина, преподаватель каф. Математические методы в экономике.

Рецензент: Е.Г. Белов, канд. физ. – мат. наук, доцент кафедры Теория управления и оптимизации.

ВВЕДЕНИЕ

Задача управления запасами возникает, когда необходимо сделать запас материальных ресурсов или предметов потребления с целью удовлетворения спроса на заданном интервале времени (конечном или бесконечном).

Исследование любой модели управления запасами, в конечном счете, должно дать ответ на два вопроса:

1. Какое количество продукции заказывать (размер заказа)?

2. Когда заказывать?

Ответ на первый вопрос обычно получается из решения задачи минимизации суммарных затрат в выбранную единицу времени. Ответ на второй вопрос зависит от типа системы контроля над уровнем запаса.

Наиболее часто используется два вида контроля над уровнем запаса: периодический и непрерывный. При периодическом контроле время заказа совпадает с одним из моментов периодической проверки. При непрерывном контроле заказ производится в момент, когда количество запаса на складе достигает вычисляемого уровня R. Величина R называется точкой заказа.

Модели управления запасами можно классифицировать следующим образом.

1. Детерминированные ¾ все параметры модели являются детерминированными величинами.

2. Вероятностные - какие – либо параметры модели являются случайными величинами.

Каждый из этих типов моделей можно разбить еще на два:

¾ стационарные (параметры модели не меняются на рассматриваемом интервале времени);

¾ динамические (некоторые параметры модели меняются на рассматриваемом интервале времени).

Наиболее важными характеристиками моделей управления запасами являются следующие.

1. Величину спроса, будем обозначать b (в рассматриваемых ниже моделях может быть постоянной детерминированной или случайной величиной, величиной зависящей от времени).

2. Сроки выполнения заказов, будем обозначать t^*.

3. Способ пополнения запасов (мгновенный или равномерный в течение некоторого интервала времени).

4. Период времени ¾ интервал, в течение которого осуществляется регулировка заказа.

5. Число пунктов накопления запаса.

6. Число видов складируемой продукции.

Перейдем к рассмотрению некоторых моделей.

Детерминированные модели

Однопродуктовая статическая модель без дефицита

Эту модель можно интерпретировать как модель управления запасами в магазине. Для упрощения задачи рассматривается только один товар. Руководство магазина закупает товар у оптовиков по цене c₁ за единицу товара, если объем закупаемой партии y меньше величины q. В случае, если объем закупаемой партии больше или равен q, делается скидка и цена единицы товара становится равной c₂ < c₁. Затраты при закупке товара состоят из двух величин. Условно постоянной величины (например, аренды автомобиля для доставки товара от оптового склада до магазина), будем называть ее стоимостью оформления заказа, и обозначать буквой K. Переменной величины ¾ стоимости закупаемой партии равной c(y)y. Здесь c(y) равно c₁,если y < q и равно c₂, если y ³ q. В рассматриваемой модели предполагается, что в магазине спрос на товар в единицу времени является величиной постоянной и принимает значение равное b.

Магазин также, несет расходы по хранению товара на собственном складе. В каждую единицу времени (час, день ит.д.) эти расходы составляют величину h за каждую единицу товара, находящуюся на складе в эту единицу времени. Можно интерпретировать эту величину как стоимость «омертвления средств» в виде товарного запаса.

После оформления заказа товар поступает на склад магазина через интервал времени длиной t^*.

Руководству нужно определить, какое количество y товара заказывать, и точку заказа R с тем, чтобы суммарные затраты в единицу времени на закупку продаваемого товара и хранение товара на складе было минимальным.

Будем считать, что величина y меняется непрерывно. Это допущение при большом объеме товара не является жестким ограничением. Затраты в рассматриваемом случае будут состоять из суммы трех величин: затрат на приобретение продаваемого товара, затрат на оформление заказа, затрат на хранение товара на собственном складе.

Можно показать [3, с. 9 – 11], что при минимальных затратах новая партия поступает на склад магазина в момент, когда весь товар израсходован. Следовательно, максимальное количество товара на складе равно y в момент поставки. График зависимости количества товара на складе от времени показан на рисунке 2. Ось x ¾ ось времени, а ось y ¾ значение величины запаса на складе.

Вычислим средние затраты в единицу времени S(y). Отметим, что это можно сделать для одного периода [0; D1], так как на остальных периодах все вычисления будут полностью совпадать.

В момент t=0 на складе имеется максимальное количество запаса равное y. В единицу времени расходуется b единиц запаса, следовательно, весь запас будет израсходован за время

t = y/b (1)

y

B

A C F

R

0 E G D1 D2 D3 t

Рис 1

За рассматриваемое время заказ будет оформляться один раз, а расходы на оформление заказа в единицу времени составят

K/ t = Kb/y. (2)

Так как величина запаса будет различной в каждую единицу времени, то и расходы по хранению будут различны. Проведем в D0В D1 среднюю линию AC и опустим перпендикуляр CE.В силу равенства треугольников DABC и DECD1, величина запаса в любой точке левее точки E больше величины 0A= y/2 настолько, насколько меньше этой величины в точке, симметричной относительно E. Поэтому на всем отрезке [0; D1] можно считать, что в среднем хранится величина y/2. Таким образом, для величины средних затрат в единицу времени получаем следующее выражение

S₁(y)= c₁β + Kb/y + hy/2, (3)

если y<q и

S₂(y)= c₂β + Kb/y + hy/2 (4)

в противном случае. Здесь первое слагаемое выражает затраты на закупку товара продаваемого магазином в единицу времени. Второе ― затраты на оформление заказа отнесенные к единице времени. Третье ― средние затраты на хранение запаса в единицу времени. Так как первое слагаемое в зависимости от y меняется один раз на постоянную величину, то минимум у этих функций достигается в одной точке.

Найдем минимум этого выражения по величине заказа y. Для этого вычислим производную и приравняем ее нулю.

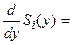- Kb/y² + h/2 = 0. i=1,2 (5)

Из равенства (5) получаем формулу экономичного размера заказа Уилсона

y^*= . (6)

Если бы цена на товар была постоянной (не зависела от объема закупаемой партии), то величина y^* была бы оптимальной. Действительно, вторая производная функции S_i(y) больше нуля в области y> 0. Следовательно, функция S_i(y) выпуклая в этой области, а точка y^* доставляет минимум этой функции.

В случае разрыва цен величина оптимальной партии y_opt зависит от величины q.

S ₁(q)

Если y^* ³ q, тогда y_opt = y^*. Так как в этом случае при закупке партии в объеме y^* будет получена скидка и суммарные затраты в единицу времени составят наименьшую из всех величину S₂(y^*). Пусть y^* < q, тогда y_opt = q, если q £ y₁. Здесь y₁ ¾ больший корень уравнения

S₁(y^*) = S₂(y). (7)

Если же q > y₁, то y_opt = y^*. Таким образом, если q £ y₁, то выгодно воспользоваться скидкой, в противном случае ¾ нет (смотри рис. 2).

Пусть оптимальный объем заказываемой партии определен и равен y_opt. Точку заказа R определяется из соотношений

R = b´t^*, t^* < t;

R = b´(t^*-m´t),

где m ¾ целая часть от деления t^* на t, а t = y_opt /b. Так на рис 1 величина t^* равна длине отрезка [ G; D ₃]. При этом m =2, а величина R показана на оси y.

Пример 1. Магазин закупает товар для продажи. Ежедневный спрос на товар в магазине ¾ 30 единиц (ед.), стоимость хранения одной единицы товара на складе составляет 0.15 денежных единиц (д.ед.), стоимость оформления заказа ¾ 100д.ед. Цена одной единицы товара 10 д.ед., если объем закупаемой партии меньше 300 ед. и 8д.ед. в противном случае. Определить объем закупаемой партии и точку заказа, если время выполнения заказа ¾ 12 суток.

Решение. Найдем y^*. По формуле (6) получаем

y^* = .

Так как y^* меньше объема q= 300, за который дают скидку, то нужно сравнить q и y₁. Найдем y₁, решая уравнение (7).

.

Приводим к общему знаменателю и решаем квадратное уравнение

.

Наибольший корень этого уравнения равен

y₁ = + .

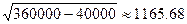Так как y₁ > q, то y_opt = q =300, следовательно,

t= y_opt /b =300/30 = 10.

Для нахождения точки заказа найдем число m = . Тогда

R= 30(12-1´10)=60.

Ответ. Необходимо заказывать 300 единиц товара, когда на складе останется 60 единиц товара.

Дата добавления: 2015-10-23