Одноэтапная модель с мгновенным спросом при отсутствии затрат на оформление заказа

Предполагается, что спрос за некоторый период времени, называемый этапом, удовлетворяется сразу в начале этапа. Удовлетворение спроса происходит за счет начального запаса и заказанной продукции, которая поступает на склад так же в начале этапа, чуть ранее момента удовлетворения спроса. Спрос является случайной величиной и имеет известный закон распределения. В зависимости от величины спроса и объема продукции на складе в начале этапа возникают либо излишки продукции (запас), либо нехватка некоторого количества продукции (дефицит). Суммарные затраты за этап складываются из затрат на закупку заказанной продукции, хранении запаса и потерь от дефицита. Введем обозначения:

x - начальный запас продукции на складе;

y - количество закупаемой продукции (величина заказа);

q - максимальный уровень запаса на складе после поставки заказа;

b - величина спроса на этапе;

h - стоимость хранения единицы продукции в течении этапа;

p - потери от дефицита единицы продукции в течении этапа;

c - стоимость закупки единицы продукции;

j (b) - функция плотности распределения вероятностей величины спроса.

При заданных величинах q и b величина запаса, который хранится на складе в течение этапа, определяется соотношением

H (q,b) = .

Величина дефицита определяется аналогичным равенством

G (q,b) = .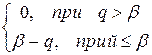

Отметим, что величины q,y,x связаны соотношением

q = y+ x (34)

При сделанных предположениях математическое ожидание суммарных затрат на этапе определяется соотношением

M { S (q)} = c (q - x) + h + p =

= c (q - x) + h + p .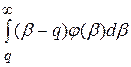

Запишем необходимое условие экстремума

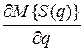= c + h 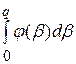- p 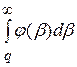= 0. (35)

Используя свойство функции плотности

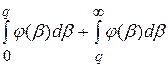= = 1,

из (35) получаем

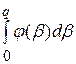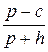= (36)

Решая уравнение (36), находим q ^*, а затем из соотношения (34) находим оптимальную величину заказа y ^* = q ^* - x. Отметим, что значение q ^* определено только при условии p ³ c. Если величина y ^* получается отрицательной, то полагаем y ^* = 0.

Пример. Пусть начальный запас равен 2 единицам, стоимость хранения единицы продукции в течение этапа - 0.5 денежных единиц, потери от дефицита одной единицы продукции в течение этапа - 4.5 денежных единиц, стоимость закупки одной единицы продукции - 0.5 денежных единиц. Функция плотности распределения вероятностей спроса имеет следующий вид

j (b) =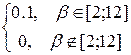

Получаем

, ,

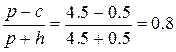следовательно, из соотношения (36) находим

q ^* = 10, y ^* = 8.

Дата добавления: 2015-10-23