Solution to Integrative problem. 1. Capital budgeting decisions involve investments requiring rather large cash outlays at the beginning of the life of the project and commit the firm to a

Читайте также:

1. Capital budgeting decisions involve investments requiring rather large cash outlays at the beginning of the life of the project and commit the firm to a particular course of action over a relatively long time horizon. As such, they are both costly and difficult to reverse, both because of: (1) their large cost; (2) the fact that they involve fixed assets which cannot be liquidated easily.

2. Axiom 5: The Curse of Competitive Markets—Why It's Hard to Find Exceptionally Profitable Projects deals with the problems associated with finding profitable projects. When we introduced that axiom we stated that exceptionally successful investments involve the reduction of competition by creating barriers to entry either through product differentiation or cost advantages. In effect, without barriers to entry, whenever extremely profitable projects are found competition rushes in, driving prices and profits down unless there is some barrier to entry.

3. Payback periodA = 3 years + years = 3.4 years

Payback PeriodB = years = 2.75 years

Project B should be accepted while project A should be rejected.

4. The disadvantages of the payback period are: 1) ignores the time value of money, 2)ignores cash flows occurring after the payback period, 3)selection of the maximum acceptable payback period is arbitrary.

5. Discounted Payback Period Calculations, Project A:

Cumulative

Undiscounted Discounted Discounted

Year Cash Flows PVIF12%,n Cash Flows Cash Flows

-$110,000	1.000	-$110,000	-$110,000
20,000	.893	17,860	-92,140
30,000	.797	23,910	-68,230
40,000	.712	28,480	-39,750
50,000	.636	31,800	-7,950
70,000	.567	39,690	31,740

Discounted Payback Period = 4.0 + 7,950/39,690 = 4.20 years.

Discounted Payback Period Calculations, Project B:

Cumulative

Undiscounted Discounted Discounted

Year Cash Flows PVIF12%,n Cash Flows Cash Flows

-$110,000	1.000	-$110,000	-$110,000
40,000	.893	35,720	-74,280
40,000	.797	31,880	-42,400
40,000	.712	28,480	-13,920
40,000	.636	25,440	11,520
40,000	.567	22,680	34,200

Discounted Payback Period = 3.0 + 13,920/25,440 = 3.55 years.

Using the discounted payback period method and a 3-year maximum acceptable project hurtle, neither project should be accepted.

6. The major problem with the discounted payback period comes in setting the firm's maximum desired discounted payback period. This is an arbitrary decision that affects which projects are accepted and which ones are rejected. Thus, while the discounted payback period is superior to the traditional payback period, in that it accounts for the time value of money in its calculations, its use should be limited due to the problem encountered in setting the maximum desired payback period. In effect, neither method should be used.

7. NPVA = 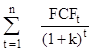- IO

= $20,000(PVIF12%, 1 year) + $30,000 (PVIF12%, 2 years)

+ $40,000(PVIF12%, 3 years) + $50,000 (PVIF12%, 4 years)

+ $70,000(PVIF12%, 5 years) - $110,000

= $20,000(.893) + $30,000 (.797) + $40,000 (.712) + $50,000

(.636) + $70,000 (.567) - $110,000

= $17,860 + $23,910 + $28,480 + $31,800 + $39,690 - $110,000

= $141,740-$110,000

= $31,740

NPVB = $40,000(PVIFA12%, 5 years) - $110,000

= $40,000(3.605) - $110,000

= $144,200-$110,000

= $34,200

Both projects should be accepted

8. The net present value technique discounts all the benefits and costs in terms of cash flows back to the present and determines the difference. If the present value of the benefits outweighs the present value of the costs, the project is accepted, if not, it is rejected.

9. PIA =

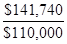
= 1.2885

PIB =

= 1.3109

Both projects should be accepted

10. The net present value and the profitability index always give the same accept reject decision. When the present value of the benefits outweighs the present value of the costs the profitability index is greater than one, and the net present value is positive. In that case, the project should be accepted. If the present value of the benefits is less than the present value of the costs, then the profitability index will be less than one, and the net present value will be negative, and the project will be rejected.

11. For both projects A and B all of the costs are already in present dollars and, as such, will not be affected by any change in the required rate of return or discount rate. All the benefits for these projects are in the future and thus when there is a change in the required rate of return or discount rate their present value will change. If the required rate of return increased, the present value of the benefits would decline which would in turn result in a decrease in both the net present value and the profitability index for each project.

12. IRRA = 20.9698%

IRRB = 23.9193%

13. The required rate of return does not change the internal rate of return for a project, but it does affect whether a project is accepted or rejected. The required rate of return is the hurdle rate that the project's IRR must exceed in order to accept the project.

14. The net present value assumes that all cash flows over the life of the project are reinvested at the required rate of return, while the internal rate of return implicitly assumes that all cash flows over the life of the project are reinvested over the remainder of the project's life at the IRR. The net present value method makes the most acceptable, and conservative assumption and thus is preferred.

15. Project A:

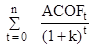$110,000 =

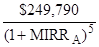
MIRRA = 17.8247%

Project B:

$110,000 =

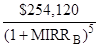
MIRRB = 18.2304%

Both projects should be accepted because their MIRR exceeds the required rate of return. The modified internal rate of return is superior to the internal rate of return method because MIRR assumes the reinvestment rate of cash flows is the required rate of return.

Solutions to Problem Set B

9-1B. (a) IO = FCFt [PVIFIRR%,t yrs]

$10,000 = $19,926 [PVIFIRR%,8 yrs]

0.502 = PVIFIRR%,8 yrs

Thus, IRR = 9%

(b) $10,000 = $20,122 [PVIFIRR%,12 yrs]

0.497 = PVIFIRR%,12 yrs

Thus, IRR = 6%

0.083 = PVIFIRR%,22 yrs

Thus, IRR = 12%

(d) $10,000 = $19,254 [PVIFIRR%,5 yrs]

0.519 = PVIFIRR%,5 yrs

Thus, IRR = 14%

9-2B. (a) IO = FCFt[PVIFAIRR%,t yrs]

$10,000 = $2,146 [PVIFAIRR%,10 yrs]

4.66 = PVIFAIRR%,10 yrs

Thus, IRR = 17%

(b) $10,000 = $1,960 [PVIFAIRR%,20 yrs]

5.102 = PVIFAIRR%,20 yrs

Thus, IRR = 19%

7.163 = PVIFAIRR%,12 yrs]

Thus, IRR = 9%

(d) $10,000 = $3,197 [PVIFAIRR%,5 yrs]

3.128 = PVIFAIRR%,5 yrs

Thus, IRR = 18%

9-3B. (a) $10,000 = + +

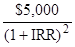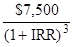
Try 21%:

$10,000 = $3,000(0.826) + $5,000 (0.683) + $7,500 (0.564)

= $2,478+ $3,415 + $4,230

= $10,123

Try 22%

$10,000 = $3,000 (0.820) + $5,000 (0.672) + $7,500 (0.551)

= $2,460 + $3,360 + $4,132.50

= $9,952.50

Thus, IRR = approximately 22%

(b) $12,000 = + +

Try 25%

$12,000 = $9,000 (0.800) + $6,000 (0.640) + $2,000 (0.512)

= $7,200 + $3,840 + $1,024

= $12,064

Try 26%:

$12,000 = $9,000 (0.794) + $6,000 (0.630) + $2,000 (0.500)

= $7,146 + $3,780 + $1,000

= $11,926

Thus, IRR = nearest percent is 25%

Try 18%

$8,000 = $2,000 (3.127) + $5,000 (0.370)

= $6,254 + $1,850

= $8,104

Try 19%

$8,000 = $2,000 (3.058) + $5,000 (0.352)

= $6,116 + $1,760

= $7,876

Thus, IRR = nearest percent is 18%

9-4B. (a) NPV = - $2,500,000

= $750,000 (4.231) - $2,500,000

= $3,173,250 - $2,500,000

= $673,250

(b) PI =

= 1.2693

3.333 = PVIFAIRR%,6 yrs

IRR = about 20% (19.90%)

(d) Yes, the project should be accepted.

9-5B. (a) Payback Period = $160,000/$40,000 = 4 years

(b) NPV = - $160,000

= $40,000 (4.355) - $160,000

= $174,200 - $160,000 = $14,200

= 1.0888

(d) $160,000 = $40,000 [PVIFAIRR%,6 yrs]

4.000 = PVIFAIRR%,6 yrs

IRR = about 13% (12.978%)

9-6B. (a) NPVA = 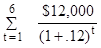- $45,000

= $12,000 (4.111) - $45,000

= $49,332 - $45,000 = $4,332

NPVB = - $70,000

= $14,000 (4.111) - $70,000

= $57,554 - $70,000 = -$12,446

(b) PIA =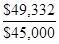

= 1.0963

PIB =

= 0.822

3.75 = PVIFAIRR%,6 yrs

IRRA = 15.34%

$70,000 = $14,000 [PVIFAIRR%,6 yrs]

5.0000 = PVIFAIRR%,6 yrs

IRRB = 5.47%

Project A should be accepted.

9-7B. (a) Project A:

Payback Period = 2 years

Project B:

Payback Period = 2 years + $1,000/$3,000 = 2.33 years

Project C:

Payback Period = 3 years + $1,000/$2,000 = 3.5 years

Project	Payback Period Method
A	Accept
B	Accept
C	Reject

9-8B. NPV9% = - $10,000,000

= $2,500,000 (5.535) - $10,000,000

= $13,837,500 - $10,000,000 = $3,837,500

NPV11% = - $10,000,000

= $2,500,000 (5.146) - $10,000,000

= $12,865,000 - $10,000,000 = $2,865,000

NPV13% = - $10,000,000

= $2,500,000 (4.799) - $10,000,000

= $11,997,500 - $10,000,000 = $1,997,500

NPV15% = - $10,000,000

= $2,500,000 (4.487) - $10,000,000

= $11,217,500 - $10,000,000 = $1,217,500

9-9B. Project A:

$75,000 = + +

+ +

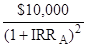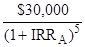
Try 10%

$75,000 = $10,000(.909) + $10,000(.826) + $30,000(.751)

+ $25,000(.683) + $30,000(.621)

= $9,090 + $8,260 + $22,530 + $17,075 + $18,630

= $75,585

Try 11%

$75,000 = $10,000(.901) + $10,000(.812) +$30,000(.731)

+ $25,000(.659) + $30,000(.593)

= $9,010 + $8,120 + $21,930+ $16,475 + $17,790

= $73,325

Thus, IRR = just over 10%

Project B:

$95,000 = $25,000 [PVIFAIRR%,5 yrs]

3.80 = PVIFAIRR%,5 yrs

Thus, IRR = just below 10%

Project C:

$395,000 = $150,000 [PVIFAIRR%,3 yrs]

2.633 = PVIFAIRR%,3 yrs

Thus, IRR = just below 7%

9-10B. (a) NPV = 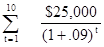- $150,000

= $25,000(6.418) - $150,000

= $160,450 - $150,000

= $10,450

(b) NPV = - $150,000

= $25,000(5.019) - $150,000

= $125,475 - $150,000

= -$24,525

(c) If the required rate of return is 9% the project is acceptable in part (a). It should be rejected in part (b) with a negative NPV.

(d) $150,000 = $25,000 [PVIFAIRR%,10 yrs]

6.000 = PVIFAIRR%,10 yrs

IRR = Between 10% and 11% (10.558%)

9-11B. (a) =

$8,000,000 =

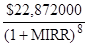
MIRR = 14.0320%

b) $8,000,000 =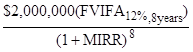

$8,000,000 =

MIRR = 15.0749%

c) $8,000,000 =

$8,000,000 =

MIRR = 16.1312%

FORD'S PINTO

(Ethics in Capital Budgeting)

OBJECTIVE: To force the students to recognize the role ethical behavior plays in all areas of Finance.

DEGREE OF DIFFICULTY: Easy

Case Solution:

With ethics cases there are no right or wrong answers - just opinions. Try to bring out as many opinions as possible without being judgmental.

Дата добавления: 2015-10-30; просмотров: 155 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
END-OF-CHAPTER PROBLEMS	\|	CHAPTER OUTLINE

mybiblioteka.su - 2015-2024 год. (0.035 сек.)