Интегрирование рациональных дробей

Определение 2. Рациональной дробью (рациональной функцией, дробно-рациональной функцией)называется выражение вида , где и – многочлены степеней и 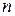соответственно.

Если степень многочлена в числителе меньше степени многочлена в знаменателе (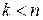), то рациональную дробь называют правильной. Если дробь неправильная (), то можно выделить в ней целую часть, представив в виде

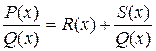, (5)

где – многочлен, и степень многочлена меньше 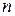, т.е. дробь является правильной.

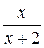Пример 10 – Рациональные дроби и – правильные. Дроби и – неправильные. Выделение целой части приводит их к виду (5): , .

Интегрирование целой части всегда легко выполняется.

Как интегрировать правильную рациональную дробь ?

Рассмотрим вначале простейшие случаи ( и 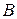– постоянные).

1. Простейшая рациональная дробь I типа

. (6)

Интеграл от неё приводится к табличному интегралу 4 подведением под знак дифференциала: .

2. Простейшая рациональная дробь II типа

(). (7)

Интеграл от дроби (7) приводится к табличному интегралу 3: .

3. Простейшие рациональные дроби III типа

(8)

и IV типа

(), (9)

в которых квадратный трёхчлен неразложим на действительные множители, т.е. его дискриминант .

Интеграл 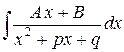от дроби (8) выделением в числителе производной знаменателя сводится к интегралу 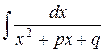, который вычисляется выделением полного квадрата в знаменателе.

Пример 11 – Найдём интеграл .

Выделяя в числителе производную знаменателя, равную , получаем: (вычисление последнего интеграла см. пример 5).

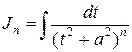Интегрирование дроби IV типа (9) является наиболее сложным и трудоёмким ([], гл.X). Выделением в числителе производной трёхчлена интеграл сводится к интегралу , который после выделения полного квадрата и замены приобретает вид . Интеграл вычисляется по рекуррентной формуле, выводимой с помощью интегрирования по частям: , .

Перейдём к вопросу интегрирования произвольной правильной рациональной дроби .

Как известно (гл.), многочлен может быть единственным образом разложен на множители вида и различной кратности, причём множители неразложимы в действительных числах (дискриминант ).

Тогда правильная рациональная дробь может быть представлена в виде суммы простейших дробей I – IV типа. При этом:

а) множителю соответствует одно слагаемое I типа ;

б) множителю соответствует сумма слагаемых I и II типов ;

в) множителю соответствует одно слагаемое III типа ;

г) множителю соответствует сумма слагаемых III и IV типов .

Постоянные , , 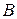…, 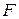в числителях простейших дробей находятся методом неопределённых коэффициентов. Для этого всю сумму простейших дробей снова приводят к общему знаменателю . Числитель полученной дроби тождественно равен многочлену . Сравнивая их коэффициенты при одинаковых степенях 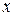, получают систему линейных уравнений для определения , , …, .

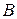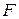Таким образом, интегрирование правильных рациональных дробей сводится к интегрированию простейших дробей I – IV типов.

Пример 12 – Найдём интеграл .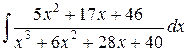

Подынтегральная дробь – правильная. Её знаменатель имеет один действительный корень и может быть представлен в виде произведения . Поэтому дробь разлагается на сумму простейших дробей .

Приводим сумму снова к общему знаменателю: .

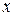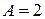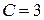Приравнивая коэффициенты при одинаковых степенях в числителях, получаем систему , из которой находим , , . Таким образом, (см. решения примеров 4 и 11).

Дата добавления: 2015-10-30