Способ непосредственного интегрирования

Первообразная и неопределённый интеграл

Определение 1. Функция называется первообразной от функции на некотором промежутке, если на этом промежутке дифференцируема и .

Отметим, что тогда .

Пример 1 – Функция является первообразной от функции , т.к. . Функция также является первообразной от функции , т.к. .

Перечислим свойства первообразных.

1. Если – первообразная от функции , то функция , где – некоторая постоянная, также является первообразной для .

2. Если и – две первообразные от функции , то они отличаются между собой на постоянную величину.

Из свойств следует, что если для функции известна какая-нибудь первообразная , то любую другую её первообразную можно представить в виде , где – постоянная. Семейство функций определяет всё множество первообразных функции .

Определение 2. Множество всех первообразных функции называется неопределённым интегралом от этой функции и обозначается символом .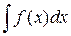

Таким образом, по определению .

Пример 2 – Из примера 1 следует, что .

Функция называется подынтегральной функцией, выражение – подынтегральным выражением, х – переменной интегрирования.

Нахождение всех первообразных данной функции называется её интегрированием.

Перечислим свойства неопределённого интеграла.

1. (или ).

2. (или ).

3. «Постоянную можно выносить за знак интеграла»:

. (1)

4. «Интеграл от суммы равен сумме интегралов»:

. (2)

Каждая формула дифференциального исчисления, устанавливающая, что , приводит к соответствующей формуле интегрального исчисления. Из таблицы основных производных получается таблица основных неопределённых интегралов, в которой в целях общности переменная интегрирования обозначается буквой .

Таблица основных неопределённых интегралов

1. (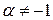) 2.

3. 4.

5. 6.

7. 8.

9. ()

9^/. ()

10. ()

10^/. ()

11.

12.

Способ непосредственного интегрирования

Пусть подынтегральную функцию можно представить в виде произведения , где – некоторая функция от 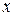. Тогда . Если интеграл является табличным: , то . Такой приём нахождения неопределённого интеграла называется подведением функции под знак дифференциала.

Пример 3 – Интеграл .

Этот же интеграл можно вычислить по-другому: .

Замечание – Пример 3 показывает, что первообразные от одной и той же функции могут весьма отличаться друг от друга, будучи, однако, связанными между собой соотношением 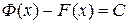вследствие свойства 2 первообразной.

В некоторых случаях перед подведением под знак дифференциала предварительно выполняются преобразования подынтегрального выражения, например, следующие:

1. Выделение целой части в подынтегральной дроби.

Пример 4 – Интеграл .

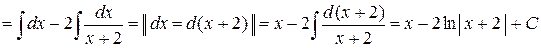2. Выделение полного квадрата в квадратном трёхчлене.

Применяется для приведения интеграла к одной из табличных форм 9 – 12.

Пример 5 – Вычислим интеграл 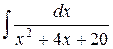. Поскольку , имеем: .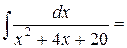

Фактически подведение функции под знак дифференциала является частью общего метода интегрирования, называемого

Дата добавления: 2015-10-30