Электр және магнит өрістерінің біртұтастығы және салыстырмалылығы

Максвелл теориясынан айнымалы электр және магнит өрістерінің арасындағы үзілмейтін байланыс ашылғаннан кейін, материяның ерекше түрі — электромагниттік өрістің бар екені айқындалды. Бұл өрістердің бір-бірінен жекеленіп, тәуелсіз түрде пайда бола алмайтыны анықталды.
Электр өрісі электр зарядтарынан немесе өзгермелі магнит өрісінің әсерінен пайда болады. Сол сияқты магнит өрісі де не электр тогының, не құйынды электр өрісінің әсерінен туады. Тұрақты өрістің дербес жағдайында не электр өрісінің ( ≠0, =0), не магнит өрісінің ( =0, ≠0) қасиеттері байқалды. Және бұл қасиеттердің білінуі таңдап алынған санақ жүйелеріне байланысты. Жібек жіпке ілінген зарядталған шарды қарастырайық. Бақылаушы жермен байланысқан санақ жүйесінде тұр. Жермен салыстырғанда тыныш тұрған зарядталған шардың тек электр өрісі бар (3.4, а-сурет). Қозғалыстағы зарядталған шардың электр өрісі кеңістікте магнит өрісін туғызады (3.4, ә-сурет).

Жалпы алғанда, айнымалы электромагниттік өрістің электр өрісінің кернеулігі мен магнит өрісі индукциясының бір-бірінен артықшылығы жоқ.

31.Құйынды электр өрісі. Тогы индукцияланатын контур қозғалыссыз тұрған,ал магнит индукциясы ағынының өзгерісі магнит өрісінің өзгерісінен болатын жағдайдағы электромагниттік индукцияны қарастырамыз.Индукциялық токтың тууы магнит өрісі өзгерісі салдарынан контурда ток тасушыларына әсер ететін тосын күштерінің пайда болуын дәлелдейді.Бұл тосын күш контурдағы химиялық процеспен де,жылулық процеспен де байланысты емес;бұлар Лоренц күші де бола алмайды,өйткені Лоренц күші зарядқа қатысты жұмыс істей алмайды.Осыдан индукциялық ток контурда туған электр өрісінен болады деп қорытындылай аламыз.Осы өрістің кернеулігін Е_в¹ деп белгілейміз. 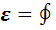Е _l ^*d l осы формула бойынша индукцияның э.қ күші контур бойынша Е_в вектор циркуляциясына тең: ε _l =∮E_Bldl (1).ε=-dф/dt формуласына сәйкес ε_i=-dф/dt=-d/dt B_ndS (2) мұндағы интеграл контурға тірелетін кез келген бетпен алынады.Контур қозғалмайтын болғандықтан,уақыт бойынша интегралдау амалының орнын төмендегідей ауыстыруға болады: d/dt 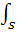B_ndS= (∂B/∂t)_ndS.(3) В векторы уақытқа да,координатқа да байланысты.(3)-теңдеудің оң бөлігін кеңістіктің өзгермейтін нүктесіне сәйкес келетін уақыт бойынша В-дан алынған туынды деп қарауға болады.Сондықтан интеграл астындағы өрнек уақыт бойынша алынған дербес туындының символы ретінде қабылданады.(2) формуланы (3)-пен ауыстырып,содан кейін ε_i-дің (1) және (2) өрнектерін теңестіріп мынаны аламыз: ∮E_Bldl=- (∂B/∂t)_ndS (4).Максвелл,уақыт бойынша тұратын магнит өрісі кеңістікте Е_В өрісінің пайда болатынын және бұл жерде өткізгіш контурдың бар-жоғына тәуелсіз болатынын болжап айтқан еді.Контурдың бар болуы тек ондағы индукциялық токтың тууы бойынша кеңістіктің сәйкес нүктелерінде электр өрісінің бар екенін табуға ғана мүмкіндік береді.

Сонымен,Максвелдің идеясы бойынша уакыт бойынша өзгеріп тұратын магнит өрісі электр өрісіе тудырады.Бұл Е_в өрісінің қозғалмайтын зарядтардан туған Е_q электростатикалық өрісінен елеулі айырмашылығы бар.Электростатикалық өріс потенциалды,оның кернеулік сызықтары зарядтарда басталып,зарядтарда аяқталады.Е_q векторының кез келген контур бойынша циркуляциясы ∮Е_qldl=0 (5).(4) формуласы бойынша Е_В векторының циркуляциясы 0-ден өзгеше.Демек,Е_В өрісі,магнит өрісі сияқты құйыңды болады екен.Е_В өрісінің кернеулік сызықтары тұйықталған болады.

Сөйтіп,электр өрісі потенциалды да (Е_q),құйынды да(Е_В) болуы мүмкін.Жалпы жағдайда электр өрісі зарядтардан туған Е_q өрісі мен уақыт бойынша өзгеріп тұратын магнит өрісінен болатын Е_В өрісінен құралады.(5) және (4) өрнектерін біріктіре қосып, Е=Е_q+E_B қосынды өрістің кернеулігі үшін төмендегідей қатысты аламыз:

∮E _ldl =- (∂B/ 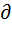t)_ndS (6).Сол бөліктегі интеграл кез келген тұйық контур бойынша, ал оң бөліктің -осы контурға тірелетін кез келген бет бойынша алынады.(6) өрнек Максвеллдің электромагниттік теориясының негізгі теңдеулерінің бірі болып табылады.

Құйынды электр өрісі электрондардың бетатрон деп аталатыниндукциялық үдеткішінде қолданылады.Бұл прибор арнайы формалы электромагнит полюстерінің арасына орналастырылған тороидты көшпелі камералардан тұрады.Электромагнит обмоткасы жиілігі 100 гц айнымалы токпен қоректенеді.Осыдан пайда болған айнымалы магнит өрісі екі функцияны орындайды:біріншіден,электрондарды үдететін құйынды электр өрісін тудырады,екіншіден,кмераның өсімен дәл келетін орбитадағы электрондарды ұстап тұрады.

32.Фуко токтары. Индукциялық токтар тұтас шомбал өткізгіштерде де қозуы мүмкін.Бұл жағдайда олар Фуко токтары немесе құйынды токтар деп аталады.Шомбал өткізгіштің электрлік кедергісі аз болғандықтан,құйынды токтар өте үлкен күшке ие бола алады.Фуко токтары Ленц ережесіне бағынады-олар өткізгіштің ішінде өздері туғызған себепке мүмкіндігінше күштірек қарсы әсер ететіндей жол және бағыт таңдап алады.Сондықтан күшті магнит өрісінде қозғалатын жақсы өткізгіштер Фуко токтары мен магнит өрісінің өзара әсерлесуінен пайда болған күшті кедергіге ұшырайды.Гальваномертлердің,сейсмографтардың және басқа приборлардың қозғалмалы бөліктерін тыныштандыру(демпфирлеу)үшін осыны пайдаланады.Прибордың қозғалмалы бөлігіне сектор түріндегі өткізгіш(мысалы,алюминий) пластинка бекітіледі,ол күшті тұрақты магнит полюстерінің арасындағы саңылауға енгізіледі.Пластинка қозғалғанда онда системаны тежейтін құйынды токтар пайда болады.Мұндай құрылғының артықшылығы мынада:тежелу тек пластинка қозғалған кезде ғана пайда болады,ал пластинка қозғалмаған кезде болмайды.Сондықтан элетромагниттік тыныштандырғыш системаның тепе теңдік қалпына дәл келуіне мүлде кедергі жасамайды.

Фуко токтарының жылулық әсері индукциялық пештерде пайдаланылады.Мұндай пеш күші үлкен,жоғары жиілікті токпен қоректенетін катушка болып табылады.Егер катушканың ішіне өткізгіш дене орналастырсақ,онда денені балқуға дейін қыздыратын интенсивті құйынды ток пайда болады.Металдарды вакуумда балқыту осындай әдіспен жүзеге асырылады,мұның өзі жоғары жиілікті материалдар алуға мүмкіндік береді.Вакуумдық қондырғылардың ішкі металдық бөліктерін газсыздандыру үшін оларды қыздыру да Фуко токтарының көмегімен жүзеге асырылады.

Көптеген жағдайларда Фуко токтарын болдырмау,әрі олармен күресу үшін арнаулы шаралар қолданіға тура келеді.Мысалы,трансформатор өзектерін құйынды токпен қыздыруға кететін энергия шығынын болдырмау үшін,бұл өзектер изоляциялаушы қабаттармен бөлінген жұқа пластинкалардан құралады.Пластинкалар Фуко токтарының мүмкін бағыттары оларға перпендикуляр болатындай етіп орналастырылады.Ферриттердің(үлкен электрлік кедергілері болатын магниттік материалдардың) пайда болуы өзектерді тұтас етіп пайдалануға мүмкіндік берді.Өн бойымен айналмалы ток агатын сымдарда пайда болатын құйынды токтар сым ішіндегі токты әлсірететіндей және бет маңындағы токты күшейтетіндей болып бағытталған.Осының нәтижесінде тез айналмалы ток сым қимасы бойынша біркелкі таралмаған болып шығады-ол өткізгіш бетіне ығыстырылған сияқты болады.Бұл құбылыс скин-эффект(ағылшынша skin-қабық) немесе беттік эффект деп аталады.Скин-эффект құбылысының болуынан жоғары жиілікті тізбектегі өткізгіштердің ішкі бөлігі пайдасыз болып шығады.Сондықтан жоғары жиілікті тізбектерде түтік өткізгіштер қолданылады.

33.Ығысу тогы. Кеңістікте өзгеретін магнит өрісінің болуы құйынды электр өрісінің тууына әкеп соғады,бұл элетромагниттік индукция құбылысын тұжырымдайды.Максвелдің негізгі идеясы электр және магнит өрістері арасында кері қатыс бар,яғни уақыт бойынша өзгеретін электр өрісі магнит өрісінің пайда болуына әкелуге тиіс деп корытындылайды.Бұл идея өте нәтижелі болды.Осы идеяның негізінде жасалған Максвелдің электромагниттік теорисы тамаша эксперименталдық қолдау тапты.

Өзгеретін электр және пайда болатын магнит өрістері арасындағы сандық қатысты орындауда Максвелдің ыгысу тогы деп аталатынды енгізді. Конденсаторы бар квазистационар айнымалы ток тізбегін қарастыралық.Еркін заряд тасушыларының қозғалысы,яғни өткізгіштік ток конденцатор астарларының арасындағы саңылаудан басқа жерде тізбектің өн бойында орын алады.Демек,өткізгіштік ток сызықтары астарлар шекарасында үзіліске ұшырайды.Оның есесіне астарлар арасындағы кеңістікте D ығысуымен сипаттауға болатын айнымалы электр өрісі пайда болады.Максвелл,өткізгіштік ток сызықтарының астарлар шекарасында,оның ығысу тогы деп аталатын ток сызықтарына үздіксіз ауысып отыратындығын болжады.Бұлай болжаудың себебі Максвелдің уақытында электр өрісі әлемдік эфир деп аталатын гипотетикалық серпімді ортадағы механикалық керілуден туады деп есептелген.Бұл керілудің нәтижесінде эфир бөлшектерінің тепе-теңдік қалыптан ығысуы болады деп ұғынған.Ток күшінің лездік мәнін i=q шамасына тең.Өткізгіштік тогының тығыздығы астар бетімен тікелей жанасқанда j_{өт=q/S=d/dt(q/S)=σ} өрнегімен анықталады,мұндағы S-астарлар ауданы,q-оның бетімен зарядталған,σ-зарядтын беттік тығыздығы.

Ығысу тогы сызықтарының жиілігі өткізгіштік ток сызықтары жиілігіндей болу үшін j_ығ ығысу тогының тығыздығы да σ-ға тең болуы керек.j_ығ-ді саңылауда бар электр өрісінің параметрлері арқылы өрнектелік.D=ε_oεE=ε_oE_o және E=σ/ε_o формулалары бойынша астарлар арасының саңылауларындағы электр ығысулары D=ε_oE_o=σ болады,бұдан σ=D.Сөйтіп,j_ығ=D (1) деп ұйғарғанымыз жөн.

Ығысу тогының тығыздығын анықтайтын (1) формуласын Максвелл кез келген турдегі электр өрісіне,соның ішінде құйынды өріске қолданды.Өткізгіштік токқа тән физикалық қасиеттердің ішінен Максвелл ығысу тогының өзінің айналасындағы кеңістікте магнит өрісін жасайтын бір ғана қасиетін алды.Максвелдің айтуы бойынша магнит өрісін формулаларда есептеуде өткізгіштік токтың тығыздығы мен ығысу тогының тығыздығынан тұратын токтың тығыздығын өрнектеу керек:j_толық=j_өт+j_ығ=j_өт+D (3).тап айтқанда,Н векторының циркуляциясы кез келген контур бойынша мынаган тең:∮H_ldl= (j_толық)_ndS= (j_өт+D)_ndS (4).Бұл теңдеу Максвелл теориясындағы негізгі екінші теңдеуді өрнектейді.(2)формуласы бойынша ығысу тогы өзгеретін электр өрісі бар жердің бәрінде болады.Демек,ол бойымен айнымалы электр тогы өтіп тұрған өткізгіштің ішінде дебар екен.Алайда өткізгіш сымның ішінде j_ығ әдетте j_өт-пен салыстырғанда ескермейтіндей аз болады.Гаусс системасында ығысу тогын анықтайтын өрнек мына түрде болады:j_ығ =1/4пD.

Дата добавления: 2015-10-29