Общая характеристика прямых методов

Федеральное государственное автономное образовательное учреждение

Высшего профессионального образования

Санкт-Петербургский

государственный университет аэрокосмического приборостроения

(ГУАП

______________________________________________________________

ЧИСЛЕННЫЕ МЕТОДЫ И ВАРИАЦИОННОЕ ВЫЧИСЛЕНИЕ

Методические указания

к выполнению лабораторных работ

Санкт-Петербург

Составители: Л.А. Мироновский, К.Ю. Петрова

Рецензенты: кафедра информационных систем СПбГУАП;

Кандидат технических наук В.М. Космачев

Содержатся указания к выполнению лабораторных работ по методам оптимизации на персональных ЭВМ с использованием программных пакетов MAPLE и MATLAB.

Методические указания предназначены для проведения лабораторных работ по курсам "Численные методы и вариационное исчисление" со студентами дневного обучения, по направлению 230100.02 «Информатика и вычислительная техника».

Подготовлены к изданию кафедрой вычислительных систем и сетей по рекомендации редакционно-издательского совета Санкт-Петербургского государственного университета аэрокосмического приборостроения.

© СПбГУАП, 2012

________________________________________________________________________

Лицензия ЛР № 020341 от 07.05.97 г. Подписано к печати

Формат 60x84 1/16. Печать офсетная. Бумага тип. № 3. Усл.-печ. 3,0

Уч.-изд. л. 2,5. Тираж 50 экз. Заказ №

________________________________________________________________________

Редакционно-издательский отдел

Отдел оперативной полиграфии

СПбГУАП

190000, Санкт-Петербург, ул. Б. Морская, 67

Лабораторная работа № 1

ЧИСЛЕННЫЕ МЕТОДЫ НУЛЕВОГО ПОРЯДКА

ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМЫХ МЕТОДОВ

К численным методам оптимизации нулевого порядка относятся вычислительные алгоритмы поиска экстремума, не использующие информации о производных целевой функции. Такие методы поиска экстремума также называются прямыми методами. По сравнению с методами более высоких порядков, они отличаются большей вычислительной устойчивостью, но, как правило, более медленной сходимостью (сходимость типичных методов нулевого порядка линейная, то есть с каждым шагом точность вычислений возрастает примерно в k раз, где константа k зависит от метода и свойств целевой функции). Кроме того, методы нулевого порядка – единственные методы, которые применимы к функциям, не имеющих производных во всех или в некоторых точках.

В данной работе рассматриваются одномерные методы оптимизации, то есть целевая функция является функцией одной переменной. Формально задача ставится следующим образом:

Задана функция одной переменной f(x), где a <= x <= b. Требуется с заданной точностью ε найти значение x 0, при котором f(x 0) минимально.

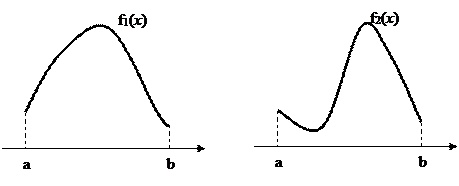
Рис. 1. Унимодальные функции. На отрезке [ a, b ] функция f₁(x) унимодальна, f₂(x) – нет.

Дата добавления: 2015-10-29