Примеры решения задач. Санкт-петербургский государственный университет

Санкт-Петербургский государственный университет

сервиса и экономики»

__________________________________________________________________

Кафедра «Химия»

Физическая

и

Коллоидная химия

Контрольная работа

для студентов-бакалавров по направлению 260800.62.

Санкт-Петербург

Одобрено на заседании кафедры «Химия» протокол №8 от 0.0. 2012 г.

Рекомендованы Учебно-методическим советом по специальности 260501.65 «Технология продуктов общественного питания»

Физическая и коллоидная химия. Контрольная работа. ¾ СПб.: ИИЦ «Сервис», 2012. ¾ 26 С.

Составитель:

канд. хим. наук, доцент О.А. Черемисина

Рецензент: зав. кафедрой «Химия», доц. Пацовский А.П.

ÓИнформационно-издательская группа «АКТиБ»

ÓСанкт-Петербургский государственный университет сервиса и

экономики

ПРАВИЛА ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа состоит из решения 7 задач, номер варианта соответствует двум последним цифрам зачетной книжки (паспорта)

Контрольная работа должна содержать титульный лист, список использованной литературы, иметь поля для замечаний преподавателя. В тексте необходимо:

1. Записать номер и полную формулировку каждого конкретного задания.

2. Дать четкие и краткие ответы по сути на теоретические вопросы.

3. При решении задач: записать условия задачи, используемые расчетные формулы в общем виде, пояснить входящие в них величины, после чего проводить вычисления, обосновывая каждое действие и соблюдая при этом соответствие размерностей используемых величин в системе

СИ.

4. Строить необходимые графики на миллиметровой бумаге и вклеивать их в работу по ходу текста.

5. В конце работы поставить дату и подпись.

Список литературы.

1. Киреев В.А. Краткий курс физической химии. - М: Химия,1978.

2. Фролов Ю.Г. Курс коллоидной химии. Поверхностные явления и дисперсные системы. - М.: Химия, 1989.

3. Липатников В.Е., Казаков К.М. Физическая и коллоидная химия: Учебник. Изд. 3-е перераб., и доп.- М.: Высшая школа, 1981.

4. Евстратов К.И., Купина Н.А., Малахова Е.Е. Физическая и коллоидная химия.- М.: Высшая школа, 1990.

Номер варианта соответствует двум последним цифрам зачетной книжки (паспорта)

ЗАДАние 1

0. 69. Химическая термодинамика как наука. Первый закон термодинамики, его формулировка и математическое выражение.

1. 70. Что называется термодинамической системой? Гомо- и гетерогенные системы. Открытые, закрытые и изолированные системы. Параметры системы. Понятия об изобарных, изотермических и изохорных процессах.

2. 71. Первый закон термодинамики для изохорного и изобарного процессов. Понятие об энтальпии. Закон Гесса и его следствия.

3. 72. Обратимые и необратимые процессы. Понятие о внутренней энергии. Математическое выражение первого закона термодинамики.

4. 73. Что называется тепловым эффектом? Связь между тепловым эффектом реакции при постоянном давлении и тепловым эффектом реакции при постоянном объеме.

5. 74. Зависимость теплового эффекта от температуры (уравнение Кирхгофа в дифференциальной и интегральной форме при Р-const).

6. 75. Термохимия. Определение теплоты реакции по правилу Гесса.

7. 76. Второй закон термодинамики. Его формулировки и математическое выражение.

8. 77. Термодинамические потенциалы. Использование термодинамических потенциалов для определения направления химической реакции.

9. 78. Теплоемкость. Истинная теплоемкость. Удельная и мольная теплоемкости.

10. 79.Теплота сгорания. Определение теплового эффекта по теплоте сгорания

11. 80. Энтропия и термодинамическая вероятность

12. 81. Процессы в неизолированных системах. Энергия Гиббса и энергия Гельмольца.

13. 82. Химическое равновесие. Закон действующих масс. Константа равновесия

14. 83. Изменение свободной энергии Гиббса и его связь с константой химического равновесия.

15. 84. Уравнение изотермы химической реакции.

16. 85. Понятие о скорости химической реакции. Средняя и истинная скорости реакции. Константа скорости и закон действующих масс.

17. 86. Химическое равновесие. Константа химического равновесия и факторы, определяющие ее величину. Правило Ле-Шателье, привести конкретные примеры его применения.

18. 87. Понятия о гетерогенной системе и фазе. Правило фаз Гиббса. Понятия о степени свободы для систем и о компоненте. Разобрать применение правила фаз Гиббса на конкретных примерах.

19. 88. Зависимость константы химического равновесия от температуры в дифференциальной форме при р-const.

20. 89. Зависимость константы химического равновесия от температуры в дифференциальной форме при V-const. Анализ зависимости lgKc = f(1/T).

21. 90. Молекулярность и порядок химической реакции. Привести примеры.

22. 91. Зависимость скорости химической реакции от температуры, правило Вант-Гоффа, температурный коэффициент реакции.

23. 92. Зависимость константы скорости химической реакции от температуры. Энергия активации. Уравнение Аррениуса.

24. 93. Катализ, основные понятия. Гомогенный катализ, механизм.

25. 94. Понятие о диаграммах состояния одно- и двухкомпонентных систем. Их практическое использование.

26. 95. Понятия об идеальных и реальных растворах. В чем их особенности? Для чего введено понятие об идеальных растворах? Перечислите способы выражения концентрации растворов.

27. 96. Растворимость газов в жидкостях. Закон Генри.Влияние температуры на растворимость газов.

28. 97. Давление пара над разбавленным раствором. Понятие об относительном понижении давления пара над растворами. Закон Рауля, его формулировка и математическое выражение.

29. 98. Кипение растворов. Причины, вызывающие понижение давления пара над растворами. Повышение температуры кипения растворов относительно чистого растворителя. Понятие об эбулиоскопической постоянной. Определение молекулярной массы растворенного вещества методом эбулиоскопии.

30. 99. Замерзание растворов. Понижение температуры замерзания растворов относительно чистого растворителя. Понятие о криоскопической постоянной. Определение молекулярной массы растворенного вещества методом криоскопии.

31. Осмос, осмотическое давление, закон Вант-Гоффа

32. Электрическая проводимость. Проводники первого и второго рода.

33. Удельная и эквивалентная электропроводность раствора, их взаимосвязь и зависимость от степени и константы диссоциации электролита

34. Электродные потенциалы и их измерение

35. Электроды сравнения. Водородный электрод.

36. Электрохимический ряд напряжений металлов, его практическое значение

37. Гальванический элемент, его ЭДС и причина его возникновения. Схема и принцип работы гальванического элемента Даниэля-Якоби.

38. Электродный потенциал, причины его возникновения. Уравнение Нернста. Факторы, влияющие на величину электродного потенциала. Стандартный электродный потенциал.

39. Концентрационные и окислительно - восстановительные цепи. Электрохимическая коррозия металлов

40. Предмет коллоидной химии. Причины особых свойств коллоидных систем. Понятия о дисперсной системе, дисперсной фазе, дисперсной среде.

41. Классификация дисперсных систем по размерам дисперсных частиц.

42. Классификация дисперсных систем по агрегатным состоянием дисперсной фазы и дисперсной среды.

43. Методы получения дисперсных систем, их классификация и краткая характеристика.

44. Степень дисперсности дисперсной фазы. Понятие об удельной поверхности. Как связана площадь поверхности дисперсной фазы с размерами и геометрической формой дисперсных частиц? Как связаны свойства коллоидных систем с изменением величины поверхности раздела дисперсной фазы и дисперсной среды?

45. Понятие о свободной поверхности энергии и причины ее появления. Рассмотрите с этих позиций устойчивость дисперсных систем. Какие процессы приводят к уменьшению и увеличению свободной поверхности энергии?

46. Молекулярно-кинетические свойства коллоидных растворов (броуновское движение, диффузия, осмос, седиментация)

47. Электрические свойства коллоидных растворов (электроосмос, электрофорез)

48. Оптические свойства коллоидных растворов. Эффект Тиндаля.

49. Строение коллоидных мицелл.

50. Адсорбционные явления в коллоидных системах. Физическая и химическая адсорбции. Типы связей между адсорбентом и адсорбтивом.

51. Адсорбция на границе твердое тело-газ. Адсорбционное урвнение Фрейндлиха.

52. Адсорбция на поверхности раздела раствор-газ. Адсорбционное уравнение Гиббса, его анализ и область использования.

53. Адсорбция на границе твердое тело-раствор. Молекулярная адсорбция из растворов. Адсорбция электролитов. Образование ДЭС.

54. Какие вещества относятся к поверхностно-активным? Описать причины и механизм проявления их поверхностной активности

55. Объяснить строение двойного электрического слоя на поверхности дисперсной частицы.

56. Объяснить механизм образования двойного электрического слоя на поверхности дисперсной частицы. Какие факторы влияют на характер его построения и на разрушение?

57. Факторы, влияющие на величину электрокинетического потенциала. Дзета – потенциал как характеристика агрегативной устойчивости золя.

58. Защита коллоидных частиц с использованием ВМС. Механизм защитного действия. Белки, углеводы, пектины как коллоидная защита.

59. Что понимается под устойчивостью дисперсной системы? Дать характеристику различным видам устойчивости дисперсным системам.

60. Что понимается под агрегативной и кинетической неустойчивостью дисперсной системы? Причины их вызывающие. Скрытая и явная коагуляции.

61. Коагуляция дисперсной системы. Скорость коагуляции. Причины, вызывающие процесс самопроизвольной коагуляции.

62. Влияние электролитов на процесс коагуляции дисперсных систем. Объяснить понятие о пороге коагуляции. Правило Шульце-Гарди.

63. Перечислить факторы, влияющие на скорость коагуляции, и обосновать механизм воздействия на коллоидные системы каждого из них.

64. Какие вещества служит стабилизаторами коллоидных систем? Пояснить механизм их влияния на агрегативную устойчивость.

65. Эмульсии. Условия их образования, классификация и свойства. Примеры эмульсий.

66. Суспензии. Условия их образования и свойства. Пасты – концентрированные суспензии. Примеры суспензий.

67. Микрогетерогенные системы. Получение и стабилизация. Примеры этих систем. Аэрозоли.

68. Пены, условия их образования и свойства. Примеры использования пен.

ЗАДАЧА 2

По значениям констант скоростей химической реакции к₁ и к₂ при температурах Т₁ и Т₂ Константу скорости к₃ при температуре Т₃

1) Энергию активации химической реакции (Е_а);

2) Константу скорости к₃ при температуре Т₃;

3) Температурный коэффициент скорости реакции γ;

вариант	Реакция	Т1,К	к1	Т2,К	к2	Т3,К	t, мин	С0, моль/л
00-01 51-53	H2 + Br2 = 2HBr		0,0856		0,00036			0,09
02-04 54-57	H2 + Br2 = 2HBr		0,0159		0,0026			0,1
05-08 58-60	H2 + J2 = 2HJ		0,00146		0,0568			2,83
09-12 61-63	2HJ = H2 + J2		0,00008		0,1059			1,87
13-15 64-67	SO2Cl2 = SO2 + Cl2		0,00006		0,0013			2,5
16-18 68-70	CO + H2O = CO2 + H2		0,00031		0,00815			3,85
19-22 71-73	COCl2 = CO + Cl2		0,0053		0,676			0,8
23-25 74-76	C2H5ONa + CH3J = C2H5OCH3 + NaJ		0,0336		2,125			0,87
26-29 77-79	C6H5CH2Br+ C2H5OH =C6H5CH2OC2H5+HBr		1,44		2,01			2,67
30-32 80-82	C12H22O11 + H2O = C6H12O6 + C6H12O6		0,765		36,0			1,85
33-35 83-85	PH3 = P(г) + 1,5H2		0,0183		0,0038			0,87
36-40 86-90	(CH2)3=CH3-СH=CH2		0,0069		0,146			1,52
41-44 91-93	CH3COOC2H5+NaOH= CH3COONa+C2H5OH		2,307		21,6			0,9
45-48 94-96	N2O5 = N2O4 + 0,5O2		0,002		0,0005			0,93
49-50 97-99	2HJ = H2 + J2		9,42·10^-7		0,0031			2,4

ЗАДАЧА 3

Используя справочные данные термодинамических свойств веществ, вы­числить для заданной реакции при заданной температуре:

1) тепловой эффект (DН°_T);

2) изменение энтропии (DS°_T);

3) изменение свободной энергии Гиббса (DG°_Т); сделать вывод о возможности протекания реакции в заданном направлении;

4) константу химического равновесия (К_р) для той реакции (прямая или обратная), которая возможна в заданных условиях

вариант	Реакция	Температура, К
00-01,51-53	2Н2 + СО = СН3ОН
02-04, 54-57	4НСI + O2 = 2H2O + 2CI2
05-08, 58-60	2N2+ 6H2O = 4NH3 + O2
09-12, 61-63	4NO + 6H2O = 4NH3 + 5O2
13-15, 64-67	CH3CHO + H2 = C2H2OH
16-18, 68-70	CO2 + H2 = CO + H2O
19-22, 71-73	2CO2 = 2CO + O2
23-25, 74-76	CO2 + 4H2 = CH4 + 2H2O
26-29, 77-79	CH4 + CO2 = 2CO + 2H2
30-32, 80-82	C2H5OH = C2H4 + H2O
33-35, 83-85	2SO2 + O2 = 2SO3
36-40, 86-90	2N2 + 6H2O = 4NH3 +3O2
41-44, 91-93	C2H6 = C2H4 + H2
45-48, 94-96	N2 + O2 = 2NO
49-50, 97-99	HCl + O2 = Cl2O + H2O

ЗАДАЧА 4

Определите давление паров воды над X% (масс.) водным раствором А при температуре Т=100ºС, считая раствор идеальным.

Вариант	X	А
00-01,27,53,79		Ацетон (CH3COCH3)
02, 28, 54, 80		Метанол (CH3OH)
03, 29, 55, 81		Глюкоза (C6H12O6)
04, 30, 56, 82		Уксусная кислота (CH3COOH)
05, 31, 57, 83		Пропиловый спирт (C3H7OH)
06, 32, 58, 84		Этиловый спирт (C2H5OH)
07, 33, 59, 85		Сахар (C12H22O11)
08, 34, 60, 86		Фруктоза (C6H12O6)
09, 35, 61, 87		Синильная кислота (HCN)
10, 36, 62, 88		Изопропиловый спирт (C3H8O)
11, 37, 63, 89		Муравьиная кислота (HCOOH)
12, 38, 64, 90		Оксид серы (VI) (SO3)
13, 39, 65, 91		Перекись водорода (H2O2)
14, 40, 66, 92		Бром (Br2)
15, 41, 67, 93		Этиловый спирт (C2H5OH)
16, 42, 68, 94		Глюкоза (C6H12O6)
17, 43, 69, 95		Ацетон (CH3COCH3)
18, 44, 70, 96		Изопропиловый спирт (C3H8O)
19, 45, 71, 97		Оксид серы (VI) (SO3)
20, 46, 72, 98		Муравьиная кислота (HCOOH)
21, 47, 73, 99		Уксусная кислота (CH3COOH)
22, 48, 74		Метанол (CH3OH)
23, 49, 75		Бром (Br2)
24, 50, 76		Синильная кислота (HCN)
25, 51, 77		Перекись водорода (H2O2)
26, 52, 78		Этиловый спирт (C2H5OH)

ЗАДАЧА 5

Вычислить потенциал электродов и ЭДС гальванического элемента при 25ºС.

Записать реакции, протекающие на электродах и в элементе, схему элемента.

Вариант	Электрод I	Электрод II
металл	раствор соли; М, моль/л	металл	раствор соли; М, моль/л
00-01,51-53	Ag	AgNO3 (0,03М)	Cd	CdSO4 (0,06М)
02-04, 54-57	Ag	AgNO3 (0,06М)	Cd	CdSO4 (0,10М)
05-08, 58-60	Ag	AgNO3 (0,09М)	Cd	CdSO4 (0,12М)
09-12, 61-63	Ag	AgNO3 (0,12М)	Cd	CdSO4 (0,14М)
13-15, 64-67	Ag	AgNO3 (0,15М)	Cd	CdSO4 (0,20М)
16-18, 68-70	Cu	CuSO4 (0,05М)	Zn	ZnSO4 (0,08М)
19-22, 71-73	Cu	CuSO4 (0,10М)	Zn	ZnSO4 (0,12М)
23-25, 74-76	Cu	CuSO4 (0,15М)	Zn	ZnSO4 (0,18М)
26-29, 77-79	Cu	CuSO4 (0,20М)	Zn	ZnSO4 (0,22М)
30-32, 80-82	Cu	CuSO4 (0,25М)	Zn	ZnSO4 (0,30М)
33-35, 83-85	Ni	NiSO4 (0,10М)	Cu	CuSO4 (0,05М)
36-40, 86-90	Cd	CdCl2 (0,10М)	Cu	CuCl2 (0,15М)
41-44, 91-93	Cu	CuCl2 (0,10М)	Fe	FeCl2 (0,05М)
45-48, 94-96	Cu	CuCl2 (0,05М)	Fe	FeCl2 (0,10М)
49-50, 97-99	Mg	MgCl2 (0,10М)	Zn	ZnCl2 (0,10М)

ЗАДАЧА 6

В таблице даны опытные данные адсорбции газа (адсорбата) на соответствующем адсорбенте:

V, м³/г ¾ объем газа, адсорбированного 1 граммом адсорбента;

Р, Па ¾ давление газа (адсорбата) над адсорбентом.

1. Построить изотерму адсорбции V = f (Р) ¾ рис.1

2. Найти графически коэффициенты Лэнгмюра, записать полученное уравнение Лэнгмюра, вычислить значения адсорбции по полученному уравнению и построить расчетную кривую V = f (Р) на том же рис.1.

Вариант	Т, К	Адсорбент	Адсорбат	Р·10^-3, Па	V·10^6, м^3/г
00-01,51-53		Уголь	N2	1,62 5,30 17,3 30,70 44,50	0,31 0,99 3,04 5,10 6,90
02-04,54-57		Уголь	CO2	4,20 8,10 11,70 16,50 24,00	12,73 21,20 26,40 32,20 38,60
05-08,58-60		Уголь	CO	9,80 24,20 41,30 60,00 72,50	2,53 5,57 8,43 11,20 12,85
09-12,61-63		Уголь	NH3	10,50 21,60 42,70 65,60 85,20	60,40 90,30 115,70 127,00 132,40
13-15,64-67		BaF2	CO	11,30 24,40 44,50 61,00 82,50	2,04 3,72 5,30 6,34 7,30
16-18,68-70		Уголь	H2	27,60 43,40 57,40 72,20 86,10	0,447 0,698 0,915 1,142 1,352
19-22,71-73	194,5	Уголь	N2	1,67 8,83 20,00 36,30 52,00	3,47 13,83 23,00 27,94 33,43
23-25,74-76	194,5	Уголь	CH4	25,60 36,70 47,80 60,50 77,00	15,20 19,10 22,30 25,30 28,40
26-29,77-79	194,5	Уголь	CO	4,00 5,34 9,65 16,65 19,80	15,80 19,05 27,70 34,10 38,95
30-32,80-82	194,5	Уголь	Ar	3,22 7,25 12,15 17,25 39,50	5,09 10,02 15,56 18,81 29,14
33-35,83-85	194,5	Уголь	CH4	25,60 36,70 47,80 60,50 77,00	15,2 19,1 22,3 25,3 28,4
36-40,86-90	194,5	Уголь	CO	4,00 5,34 9,65 16,65 19,80	15,80 19,05 27,70 34,10 38,95
41-44,91-93	194,5	Уголь	Ar	3,22 7,25 12,15 17,25 39,50	5,09 10,02 15,56 18,81 29,14
45-48,94-96		Уголь	C2H4	9,35 12,45 22,50 42,60 82,50	39,5 42,8 49,9 56,5 64,5
49-50,97-99		Уголь	C2H4	2,00 4,27 10,57 29,5 91,5	10,4 20,8 30,5 42,4 55,2

ЗАДАЧА 7

Напишите формулы мицелл золей, полученных сливанием равных объемов растворов электролитов указанной концентрации. Приведите название всех слоев мицеллы. Укажите место возникновения дзета-потенциала (z). Укажите заряд частицы.

Вариант	Электролиты, молярная концентрация эквивалента (нормальность)
I	II
00-01,51-53	0,01H KJ	0,001H AgNO3
02-04, 54-57	0,001H KJ	0,01H AgNO3
05-08, 58-60	0,01H KCl	0,001H AgNO3
09-12, 61-63	0,001H KCl	0,01H AgNO3
13-15, 64-67	0,03H AgNO3	0,001H KBr
16-18, 68-70	0,001H NaBr	0,01H AgNO3
19-22, 71-73	0,01H LiJ	0,005H AgNO3
23-25, 74-76	0,05H AgNO3	0,001H LiJ
26-29, 77-79	0,01H RbBr	0,0005H AgNO3
30-32, 80-82	0,0004H RbBr	0,01H AgNO3
33-35, 83-85	0,01H BaCl2	0,005H H2SO4
36-40, 86-90	0,05H H2SO4	0,1H BaCl2
41-44, 91-93	0,1H FeCl3	0,05H K4[Fe(CN)6]
45-48, 94-96	0,01H FeCl3	0,01H K4[Fe(CN)6]
49-50, 97-99	0,01H KJ	0,05H AgNO3

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ЗАДАЧА 2

По значениям констант скоростей химической реакции k₁ и k₂ при температурах Т₁ и Т₂ определите:

1) энергию активации химической реакции (Е_а);

2) константу скорости k₃ при температуре Т₃;

3) температурный коэффициент скорости реакции (γ);

4) количество вещества (%), израсходованное за время t при температу­ре Т ₃, если начальные концентрации веществ равны С₀ (считать, что порядок реакции и молекулярность совпадают).

ДАНО:

Реакция 2NО₂ → N₂ + 2О₂

Т₁ = 986К k₁ = 6,72 мин^-1 (моль/л)^-1

Т₂ =1165К k₂ = 977,0 мин^-1 (моль/л)^-1

Т₃ =1053,2К t=10 мин

С₀ ⁼ 1,75 моль/л

РЕШЕНИЕ:

1) Определяем энергию активации (Е_а), используя уравнение Аррениуса в та­кой форме:

(1)

где k₁ и k₂ - константы скорости реакции при температурах Т₁ и Т₂

Е_а - энергия активации химической реакции, кДж/молъ; R - универсальная газовая постоянная, R= 8,314 Дж/(молъ´К).

Отсюда

Е_а = 266,4 кДж/молъ.

2) Найдем константу скорости k₃при температуре Т₃, используя то же уравне­ние (1):

Отсюда

k₃ = 52,54 мин^-1 (моль/л)^-1

3) Найдем температурный коэффициент скорости реакции из уравнения (правило Вант-Гоффа):

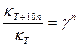(2)

где k_Т и k_Т+10n - константы скорости при температуре Т и (Т + 10n); γ - температурный коэффициент скорости реакции; n -показатель степени, вычисляется по разности температур опыта, деленной на 10:

(3)

Для заданной реакции имеем:

(4)

Отсюда

γ =1,32.

4) Далее определим количество вещества (%), израсходованное за 10 мин от начала реакции, если начальная концентрация NО₂ составляла 1,75 моль/л. Считаем, что порядок реакции и молекулярность равны двум. Запишем уравнение для константы скорости реакции второго порядка:

(5)

где С - концентрация вещества, оставшаяся не израсходованной к моменту времени t от начала реакции.

Отсюда

С = 1,9´10^-3 моль/л,

что составляет 0,11% от исходной концентрации NО₂ (С₀ = 1,75 моль/л).

Следовательно, при Т = 1053,2К за 10 мин от начала реакции израсходо­валось 99,89% NО₂.

ЗАДАЧА 3

Используя справочные данные термодинамических свойств веществ, вы­числить для заданной реакции при заданной температуре:

1) тепловой эффект (DН°_T);

2) изменение энтропии (DS°_T);

3) изменение свободной энергии Гиббса (DG°_Т); сделать вывод о возможности протекания реакции в заданном направлении;

4) константу химического равновесия (К_р) для той реакции (прямая или обратная), которая возможна в заданных условиях.

ДАНО:

Реакция 2NО₂ → 2NO +О₂

Т= 400К

Для решения задачи требуются справочные данные термодинамических свойств веществ - участников реакции. Сведем эти данные в таблицу:

Вещество	DН°f,298, кДж/моль	S°298, Дж/(моль´К)	Сºр,298 Дж/(моль´К)
NО2	34,19	240,06	32,66
NO	91,26	210,64	29,86
O2		205,04	29,37

РЕШЕНИЕ:

1) По закону Кирхгофа (сокращенное уравнение)

DН°_T = DН°₂₉₈ +DСº_р,₂₉₈(T-298) (6)

где DН°_T и DН°₂₉₈ - тепловые эффекты химической реакции при температуре Т и стандартной температуре (298К), соответственно, кДж;

DСº_р,₂₉₈ - изменение теплоемкости системы в ходе химической реакции, Дж/К.

DН°₂₉₈ вычисляется по первому следствию из закона Гесса:

DН°₂₉₈ = Sn_iDН°_f,298(продукты реакции) - Sn_iDН°_f,298(исходные вещества) (7)

где DН°_f,298 - стандартная теплота образования вещества, кДж/моль;

n_i - стехиометрические коэффициенты в уравнении реакции.

DСº_р,₂₉₈ вычисляется по уравнению, аналогичному уравнению (7):

DСº_р,₂₉₈ = Sn_i Сº_р,₂₉₈ (продукты реакции) - Sn_i Сº_р,₂₉₈ (исходные вещества) (8)

где Сº_р,₂₉₈ - теплоемкость веществ-участников реакции в стандартных условиях, Дж/(моль´К)

Для данной реакции:

DН°₂₉₈ = 2DН°_f,298(NO) + 2DН°_f,298(O₂) - 2DН°_f,298(NO₂)

DН°₂₉₈ = 2·91,26 + 0 - 2·34,19 = 114,14 кДж

DСº_р,₂₉₈ = 2·29,86 + 29,37 - 2·36,66 = 15,77 Дж/К

DН°_T = 114,14 + 15,77(400-298)·10^-3 = 115,749 кДж

2) Изменение энтропии (DS°_T) вычисляется по уравнению:

(9)

где DS°_T и DS°₂₉₈ изменение энтропии химической реакции при температуре Т и стандартной (298), Дж/К;

DСº_р,₂₉₈ - изменение средней теплоемкости веществ в ходе химической реакции при стандартной температуре (298К), Дж/К.

Изменение энтропии в стандартных условиях (DS°₂₉₈) вычисляется по уравнению, аналогичному уравнению (7):

DSº₂₉₈ = Sn_i Sº₂₉₈ (продукты реакции) - Sn_i Sº₂₉₈ (исходные вещества)

(10)

где Sº₂₉₈ - абсолютные энтропии веществ-участников реакции в условиях, Дж/(моль-К).

Для заданной реакции:

DSº₂₉₈ = 2·210,64 + 205,04 - 2·240,06 = 146,2 Дж/К.

Теперь вычислим DS°_T по уравнению (9):

= 150,84 Дж/К. 298

3) Изменение свободной энергии Гиббса (DG°_Т) находят по уравнению Гиббса-Гельмгольца:

DG°_Т = DН°_T - ТDS°_T; (11)

Для заданных условий

DG°_Т = 115749 - 400·150,83 = 55417 Дж.

Вывод о возможности протекания заданной реакции в заданных условиях: критерием возможности протекания процесса является условие

DG°_Т < 0 (12),

т.е в ходе процесса свободная энергия Гиббса должна уменьшиться.

В нашем случае DG°_Т > 0, что говорит о невозможности (с точки зрения химической термодинамики) протекания прямой реакции. Эта же величина DG°_Т. для обратной реакции составит -55417 Дж (DG°_Т = -55417 Дж), т.е. в заданных условиях возможна обратная реакция.

4) Вычислим для обратной реакции константу химического равновесия (К_р) по уравнению:

DG°_Т = -RTlnK_p (13)

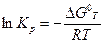(14)

где R — универсальная газовая постоянная, К. = 8,3 14 Дж/(молъ´К).

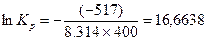
K_p = 1,73´10⁷.

ЗАДАЧА 4

Определите давление паров воды над 5% (мае.) водным раствором фруктозы (С₆Н₁₂О₆) при температуре Т=100°С, считая раствор идеальным.

Решение.

Для идеальных растворов справедливо уравнение Рауля:

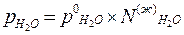(15)

где P_H2O - давление паров воды над водным раствором (фрукто­зы) при данной температуре

Т= 100 °С; P_H2O - давление паров воды над чистой водой при данной температуре Т = 100 °С; N^(ж)_H2O - мольная доля воды в данном растворе фруктозы.

Любая жидкость закипает при температуре, когда давление паров над жидкостью становится равным внешнему давлению. Известно, что если внешнее давление равно 1 атм (10⁵ Па) чис­тая вода кипит при Т = 100 °С. Следовательно, P⁰_H2O = 10⁵Па.

Мольная доля данного компонента раствора рассчитывает­ся по уравнению:

,

где п - число молей данного компонента; S n - сумма чисел молей всех компонентов в растворе.

Для данной задачи:

(16)

Пусть имеем 100 г раствора. В нем содержится 5 г фрукто­зы и 95 г воды. Молярная масса фруктозы М(С₆Н₁₂О₆) =180 г/моль.

Число молей определяется по уравнению:

,

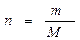где т - масса данного компонента в граммах. В 100 г раствора содержится:

молей H₂O

молей фруктозы

Сумма молей S n = 5,278 + 0,028 = 5,306 молей.

Мольная доля воды в данном растворе рассчитывается из уравнения (16):

Давление паров над 5% (масс) водным раствором рассчи­тывается из уравнения (15):

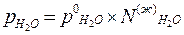= 10⁵ Па · 0,995= 9,95·10⁴ Па.

ЗАДАЧА 5

Вычислить потенциалы электродов и ЭДС гальванического элемента при 25°С. Записать реакции, протекающие на электродах и в элементе, схему эле­мента.

ДАНО:

Электрод I: металл ¾ Fe(II) электролит ¾ FeCl₂(0,1M)

Электрод II: металл ¾ Mg электролит ¾ МgSО₄ (0,05М)

РЕШЕНИЕ:

Реакции на электродах: Fе²⁺ + 2ē Û Fe

Mg²⁺ + 2ē Û Mg

Чтобы определить, как протекает реакция в элементе, необходимо знать потенциалы электродов, из которых составлен гальванический элемент.

Потенциалы для электродов I рода, к которым относятся к металлические электроды, вычисляются по уравнению Нернста:

(17)

где j_Ме/Меⁿ⁺ - потенциал металлического электрода в заданных условиях, В

j⁰_Ме/Меⁿ⁺ - стандартный электродный потенциал, т.е потенциал электрода при условии

a_Меⁿ⁺ =1 B; находится по справочным таблицам;

R - универсальная газовая постоянная, R = 8,314 Дж/(моль´К);

Т-температура, К;

n - число электронов, участвующих в обратимо протекающей окислительно-восстановительной реакции на электроде;

F - число Фарадея (F = 96500 Кл);

а_Меⁿ⁺ - активность ионов металла в растворе, моль/л.

На практике часто для вычисления потенциалов электродов уравнение Нернста используется в более простой форме, а именно: вместо активности ионов металла (а_Меⁿ⁺) используется их концентрация (C_Меⁿ⁺), слагаемое 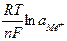после подстановки в него значений R, Т, F и перевода натурально­го логарифма в десятичный, для стандартной температуры Т = 298 K запишется в виде . Таким образом, уравнение (17) запишется в виде:

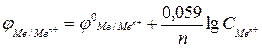
Используя это уравнение, вычислим потенциалы заданных электродов:

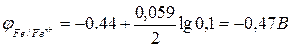
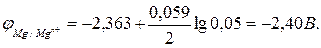
Из полученных значений потенциалов электродов следует, что реакция в гальваническом элементе протекает по схеме:

Mg + Fе²⁺ Û Mg²⁺ + Fe

Электродвижущая сила гальванического элемента вычисляется как раз­ность потенциалов электродов, причем ЭДС должна быть всегда положитель­ной величиной.

E = j_Fe/Fe²⁺ - j_Mg/Mg²⁺

Е = -0,47 + 2,40 = 1,93 В.

Схема элемента:

(-) Mg,Мg²⁺ (0,05М) | Fе²⁺ (0,1М), Fе (+).

ЗАДАЧА 6

В таблице даны опытные данные адсорбции газа (адсорбата) на соответ­ствующем адсорбенте:

V, м³/г - объем газа, адсорбированного 1 граммом адсорбента;

Р, Па - давление газа (адсорбата) над адсорбентом.

1. Построить изотерму адсорбции V = f (Р) - рис. 1.

2. Найти графически коэффициенты уравнения Лэнгмюра, записать получен­ное уравнение Лэнгмюра, вычислить значения адсорбции по полученному уравнению и построить расчетную кривую V = f (Р) на том же рис. 1.

Т, К	Адсорбент	Адсорбат	Р´10 ^3, Па	V´ 10^3, м^3/г
			2,0	10,4
			4,27	20,8
	Уголь	С2Н4	10,57	30,5
			29,5	42,4
			91,5	55,2

РЕШЕНИЕ:

1) Построим изотерму адсорбции V = f (Р) по опытным данным (рис. 1, кривая 1, точки ·).

2) Уравнение Лэнгмюра для адсорбции газа записывается в виде:

(18)

где Г - количество газа-адсорбата, адсорбированное 1 г адсорбента (или 1 см³ его поверхности) в заданных условиях;

Г_¥ — максимальное количество газа-адсорбата, адсорбированное 1 г адсорбента (или 1 см³ его поверхности) в заданных условиях;

Р - равновесное давление газа-адсорбата.

Количество газа-адсорбата удобно измерять в виде объема (V). Тогда уравнение (18) запишется в виде:

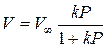(19)

где V и V_¥ имеют тот же смысл, что и Г и Г_¥ в уравнении (18).

Коэффициентами уравнения Лэнгмюра являются V_¥ и k. Чтобы графиче­ски найти эти коэффициенты, уравнение Лэнгмюра необходимо линеаризовать (привести к линейной форме):

(20)

Затем строится график зависимости и по графику полученной прямой линии находят коэффициенты V_¥ и k. Зависимость предcтавлена на рис. 2 в соответствии с данными таблицы:

Таблица

Данные для вычисления величины адсорбции С₂Н₄ на угле

по уравнениям (20, 22)

		V´10^6, м^3/г, вычисленный по уравнению (22)
5,00	96,2	10,5
2,34	48,1	18,5
0,95	32,8	30,7
0,34	23,6	43,1
0,11	18,1	51,0

По представленному на рис. 2 графику прямой линии находим коэффициенты уравнения Лэнгмюра V_¥ и k.

Из графика = 18,0. Отсюда V_¥ = 55,55´10^-6 м³/г.

Из графика tgα = 15,4´10⁷, из уравнения (20) , следовательно,

Подставим найденные значения коэффициентов в уравнение (19) и запишем выражение для вычисления V = f (Р) по уравнению Лэнгмюра:

(21)

или

(22)

Вычислим V по уравнению (22), запишем полученные расчетные данные таблицу 1 и нанесем полученные точки в координатах V — Р на рис. 1 (кривая точки ▪).

Поскольку опытная кривая 1 и расчетная кривая 2 на рис. 1 совпадают, сделаем вывод о правильности найденных коэффициентов уравнения Лэнгмюра.

Рис. 1 Изотерма адсорбции V = f (Р) С₂Н₄ на угле при 293 К

кривая 1 (·) - опытные данные

кривая 2 (▪) - значения V = f (Р), найденные по уравнению Лэнгмюра (19, 22)

Рис. 2 Зависимость для нахождения коэффициентов Лэнгмюра (19)  

ЗАДАЧА 7

Напишите формулу мицеллы золя, полученного сливанием равных объемов растворов 0,02Н AgNO₃ и 0,01Н KCl.

Приведите название всех слоев мицеллы.

Укажите место возникновения дзета-потенциала (ζ-потенциала)

Укажите заряд частицы.

Решение:

В заданных условиях методом химической конденсации получается золь хлорида серебра:

AgNO₃ + KCl = AgCl¯ + KNO₃

Поскольку электролит AgNO₃ находится в системе в избытке, то ионы Ag⁺ будут для полученного золя потенциалопределяющими, а ионы NO₃^- ¾ противоионами.

Запишем формулу мицеллы золя:

+

Дата добавления: 2015-10-29