Теоретические сведения. 1. 2. Применение вариационного исчисления

1.2. Применение вариационного исчисления

Методы Ферма и Лагранжа позволяют аналитически решать конечномерные экстремальные задачи, когда критерий зависит от конечного числа неизвестных. Более трудны для решения бесконечномерные экстремальные задачи, когда критерий зависит от неизвестной функции f (x). Такие задачи решают методами вариационного исчисления.

Простейшая задача вариационного исчисления формулируется следующим образом. Требуется найти кривую y = f (x), проходящую через две заданные точки A(x ₁, y ₁), В(x ₂, y ₂) и доставляющую экстремум функционалу

(1)

В курсе вариацинного исчисления доказывается, что искомая кривая удовлетворяет т. н. уравнению Эйлера:

(2)

где через и обозначены частные производные от подынтегральной функции

Уравнение Эйлера (2) представляет собой нелинейное дифференциальное уравнение второго порядка, семейство решений которого содержит экстремальную кривую y = f (x).

Следует заметить, что уравнение Эйлера не дает окончательного решения поставленной задачи, а лишь выделяет класс кривых, подозрительных на экстремум. Ситуация здесь вполне аналогична поиску экстремума функции путем ее дифференцирования, когда экстремум может оказаться либо в одной из точек, где производная равна нулю, либо на краях интервала.

Общее решение уравнения (2) зависит от двух произвольных постоянных y = f (x, C₁, C₂) и задает двухпараметрическое семейство экстремалей. Для определения постоянных C₁, C₂ и выделения из семейства экстремалей одной кривой – решения исходной задачи – используют краевые условия

В простейшей задаче вариационного исчисления левая и правая точки искомой кривой фиксированы. В общем случае эти точки могут лежать на заданных кривых, тогда говорят о вариационной задаче с подвижными границами.

Пусть левая точка А находится на кривой j(x), а правая точка В – на кривой y(x) (рис. 1).

Рис. 1

Рассмотрим случай, когда в качестве функционала (1) выступает длина кривой y = f (x), соединяющей кривые j и y, т.е. он имеет вид: К минимизации такого критерия сводятся разнообразные задачи о расстоянии между точками, прямыми и кривыми.

Уравнение Эйлера (2) в этом случае принимает простой вид (покажите это!), его решения (экстремали) – прямые линии y = kx + b. Это соответствует очевидному геометрическому факту, что кратчайшие пути на плоскости – отрезки прямых.

Для определения постоянных k, b привлекают так называемые условия трансверсальности.

Они имеют вид

(3)

Одно из них относится к левому концу искомой кривой у, другое – к правому.

Найдем условия трансверсальности для задачи о минимальном расстоянии между кривыми j(x) и y (x) (рис. 3). Их можно получить непосредственно по формулам (3), подставляя в них (сделайте это!), однако проще поступить следующим образом. Обозначим концы произвольного отрезка АВ, соединяющего эти кривые, через A(x ₁, y ₁), В(x ₂, y ₂). Координаты точек А, В должны удовлетворять условиям

y ₁ = j(x ₁); у ₂ = y(x ₂). (*)

Нам нужно из всех возможных отрезков АВ выбрать самый короткий, для которого квадрат расстояния минимален. Дифференцируем критерий по x ₁ и x ₂ и выписываем условия экстремума Учитывая, что согласно формулам (*) получаем:

(4)

Это и есть условия трансверсальности для данной задачи. Из них, в частности, следует, что экстремальная прямая должна быть одновременно ортогональна обеим кривым j(x) и y(x).

Пример 3. Определим минимальное расстояние между параболой и окружностью из примера 2 вариационными средствами. Решением уравнения Эйлера для этого случая является отрезок прямой

(5)

Найдем условия трансверсальности для обоих концов отрезка. Уравнение параболы имеет вид следовательно

Подставляем эти выражения в первое из уравнений (4):

Это условие трансверсальности для левого конца отрезка, лежащего на параболе.

Чтобы найти аналогичное условие для правого конца, выписываем уравнение окружности и дифференцируем его:

Подставляем найденную производную во второе из уравнений (4):

Это второе условие трансверсальности. Добавим еще два уравнения

описывающие, что концы отрезка АВ лежат на параболе и окружности.

В итоге имеем систему из четырех уравнений с четырьмя неизвестными k, b, x 1, x 2:

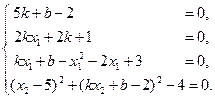
(6)

Ее можно решить вручную. Выразим из первого уравнения , из второго – и подставим их в остальные уравнения:

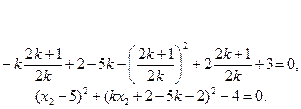
Первое из этих уравнений после умножения на 4 k 2 приводится к виду

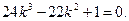
Левую часть можно разложить на множители

.

Отсюда находим три значения коэффициента наклона прямой:

Подставляя найденные значения k в первое уравнение системы (6), находим три значения b

Графики трех прямых (5), соответствующих этим значениям k, b, показаны на рис. 2. Все они проходят через центр окружности (и поэтому ортогональны к ней) и ортогональны одной из ветвей параболы. Убедимся, например, что средняя прямая ортогональна параболе в точке Вычисляем угловой коэффициент наклона касательной к параболе в этой точке:

В то же время наклон прямой равен k ₁=1/4, т.е. выполняется стандартное условие ортогональности прямых

Из рис. 2 видно, что минимальное расстояние d дает прямая с отрицательным коэффициентом наклона, т.е. решение задачи имеет следующий вид:

,

.

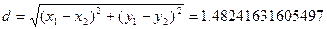Это совпадает с решением, полученным методом неопределенных множителей Лагранжа.

ЗАДАНИЕ ПО РАБОТЕ И СОДЕРЖАНИЕ ОТЧЕТА

В данной работе, также как и в работе № 2, требуется вычислить расстояние между двумя алгебраическими кривыми 2-го порядка. В случае, если фигуры пересекаются, путем переноса центра окружности и/или поворота одной из парабол или гипербол добиться того чтобы фигуры не пересекались. При этом следует привести исходные и результирующие уравнения, а также указать, на какой угол был осуществлен поворот. Затем необходимо вычислить расстояние между фигурами используя вариационный подход и условия трансверсальности.

Вращение фигуры на плоскости осуществляется следующим образом. Предположим, исходная фигура задана уравнением . Для того, чтобы повернуть ее вокруг начала координат на угол против часовой стрелки нужно осуществить подстановку .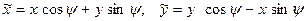

Отчет по работе должен содержать:

1. Уравнение, описывающее две заданные фигуры, их чертеж. Если фигуры пересекаются, то привести уравнения и чертеж измененных фигур вместе с текстом программы в MAPLE для получения преобразованных уравнений.

2. Поиск кратчайшего расстояния средствами вариационного исчисления. Уравнение Эйлера, его решение средствами MAPLE. Вывод уравнений трансверсальности. Чертеж, содержащий две фигуры, экстремальные прямые и точки их пересечения с фигурами.

3. Сравнение результатов, полученными двумя методами. Координаты точек пересечения искомой прямой с обеими фигурами. Уравнение, описывающее эту прямую.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Найти расстояние между параболой y = x ² и прямой x – y =5 с помощью вариационного исчисления.

2. Найти расстояние от точки A(1,0) до эллипса 4 x ²+9 y ²=36 с помощью вариационного исчисления.

3. Выписать и решить уравнение Эйлера для функционалов:

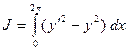а) ; б) ; в)

4. Найти условия трансверсальности (4), используя формулы (3).

5. Показать, что из уравнений (4) следует ортогональность отрезка АВ кривым j и y.

6. Найти углы между прямыми (рис. 4) и касательными к параболе.

ВАРИАНТЫ ЗАДАНИЙ

№
Фигура 1	С1	C1	C1	C1	C1	C1	C1	C3	C3	C3
Фигура 2	P1	P2	P3	P4	H1	H2	H3	H1	H2	H3

№
Фигура 1	С2	C2	C2	C2	C2	C2	C2	C3	C3	C3
Фигура 2	P1	P2	P3	P4	H1	H2	H3	P1	P2	P4

В каждом варианте требуется найти расстояние между двумя заданными фигурами.
Уравнения фигур приведены ниже:

С1: (x-5)^2+(y-10)^2=16	С2: (x-7)^2+y^2=9
С3: (x-7)^2+y^2=9	P1: y-x^2/8-2*x+3
P2: y-x^2+16	P3: y+x^2-x
P4: 2*y-x^2+3	H1: y^2-x^2-x*y+7*x
H2: 5*y^2-x^2+9	H3: y^2-x^2/10-2*x*y-x-y

[1] Постарайтесь объяснить, какова разница между этими способами, и какой из них предпочтительней

Дата добавления: 2015-10-29