
Читайте также:
|
Общая форма критерия вытекает из основного постулата исследования операций: оптимальное решение — это решение поставленной задачи либо с минимумом материальных затрат, либо при фиксированных материальных затратах с максимальной эффективностью.
Пусть эффективность операции О, т. е. управляемого мероприятия, на исход которого можно в какой-то мере влиять, выбирая, тем или иным способом параметры, характеризуется каким-то численным критерием или показателем W который требуется обратить в максимум (минимум). Предположим, что математическая модель ее, позволяющая вычислить этот показатель ‚ при любом принятом решении, построена.
На практике возможны два решения:
когда факторы, влияющие на исход операции, либо заранее известны, либо зависят от нас и, притом, не все условия выполнения операции известны, а некоторые из них содержат элемент неопределенности.
Рассмотрим сначала наиболее простой случай.
Факторы, от которых зависит успех операции, делятся на две группы: заданные заранее α1, α2, α3..., на которые влиять нельзя; зависящие (элементы решения) х1, х2, х3 ..., которые можно выбирать по своему усмотрению.
Под заранее известными факторами α1, α2, α3... и элементами решения х1, х2, х3 ... можно понимать не только обычные числа, но и функции, в частности — ограничения, наложенные на элемёнты решения. Показатель эффективности W зависит от обеих групп факторов и это символически выражается так:

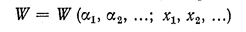
Поскольку математическая модель построена, будем считать, что приведенная выше зависимость известна, и для любых α1, α2, α3 и х1, х2, х3 ... её можно найти.
Задача исследования операций математически формулируется следующим образом: при заданных условиях с α1, α2, α3 требуется найти такие элементы решения х1, х2, х3 ...., при которых показатель эффективности W обращается в максимум (минимум).
В рассматриваемом детерминированном случае отыскание оптимального решения сводится к отысканию максимума или минимума (короче, экстремума) функции W. Эта задача может быть очень сложной (особенно когда аргументов много), но ее удается так или иначе решить до конца.
Для решения практических задач исследование операций располагает арсеналом математических средств: теория вероятностей с ее новейшими разделами, теория информации, теория массового обслуживания, математические методы оптимизации, начиная с простейших способов нахождения экстремума и кончая современными, (такими, как линейное программирование, динамическое программирование и др.) – всё это имеется в распоряжении.
Когда не все условия, в которых проводится операция, известны заранее, эффективность ее зависит уже не от двух факторов, а от трех: условий выполнения α1, α2, α3, которые известны заранее и изменены быть не могут; неизвестных условий У1 У2...; элементов решения х1, х2,..., которые предстоит выбрать.
Эффективность операции, характеризующаяся некоторым показателем W, зависящим от всех трех групп факторов, записывается в следующем виде:

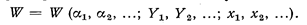
Так как параметры 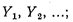 ... неизвестны, то неизвестен и зависящий от них показатель эффективности W при любом решении. Это переводит задачу в другую категорию — выбор решения в условиях не определенности.
... неизвестны, то неизвестен и зависящий от них показатель эффективности W при любом решении. Это переводит задачу в другую категорию — выбор решения в условиях не определенности.
Формулировка ее следующая: при заданных условиях α1, α2, α3 с учетом неизвестных факторов 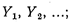 найти такие элементы решения х1, х2, х3 ... которые, по возможности обращали бы в максимум показатель эффективности W.
найти такие элементы решения х1, х2, х3 ... которые, по возможности обращали бы в максимум показатель эффективности W.
Наиболее прост и благоприятен для расчетов случай, когда неизвестные факторы У1, У2... представляют собой случайные величины со статистическими данными, характеризующими их распределение.
Тогда для оптимизации решения можно использовать один из двух приемов: искусственный перевод вероятностного характера явления к детерминированной схеме; оптимизация в среднем. Первый сводится к тому, что неопределенную, вероятностную картину явления приближенно заменяют детерминированной, т. е. все случайные факторы У1, У2.. — не случайными (обычно их математическими ожиданиями).
Этот прием применяют преимущественно для грубых, ориентировочных расчётов.
Наиболее труден для исследования случай неопределенности, когда неизвестные факторы У1 , У2... нельзя изучить и описать статистическими методами. Тогда вместо произвольного и субъективного назначения вероятностей, с дальнейшей оптимизацией в среднем, рекомендуется рассмотреть весь диапазон возможных значений У1 , У2 и составить представление о том, какова эффективность операции в это диапазоне, и как на нее влияют неизвестные условия.
При обосновании решения в условиях неопределенности, какие бы действия ни производились, элемент неопределенности остается.
И поэтому вместо того чтобы после расчетов указать одно единственное решение, всегда лучше выделить область приемлемых решений, из которой ответственные лица могут сделать окончательный выбор.
Из всего вышеизложенного следует, что своеобразие системного подхода в ИСО состоит в том, что всегда оценивается практическая приемлемость результата во времени и допускаемая погрешность от упрощения задач.
То есть действует принцип: «раз невозможного хочу я – я и возможного лишён». Риск от такого системного подхода невелик, поскольку есть опыт применения традиционных схем исследования.
Дата добавления: 2015-10-29; просмотров: 76 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Выбор формы кривой (тренда) | | | Chapter One: This City//Last Night |