Выбор формы кривой (тренда)

Выбор моделей прогнозирования базируется на оценке их ка­чества. Независимо от метода оценки параметров моделей экстраполяции (прогнозирования) их качество определяется на основе исследования свойств остаточной компоненты — (у, — y_Ti), i =\,n, т.е. величины расхождений на участке аппроксимации (построения модели) между фактическими уровнями и их расчет­ными значениями.

Качество модели определяется ее адекватностью исследуемо­му процессу и точностью. Адекватность характеризуется наличи­ем и учетом определенных статистических свойств, а точность — степенью близости к фактическим данным. Модель прогнозиро­вания будет считаться лучшей со статистической точки зрения, если она является адекватной и более точно описывает исходный динамический ряд.

Модель прогнозирования считается адекватной, если она учитывает существенную закономерность исследуемого процес­са, в ином случае ее нельзя применять для анализа и прогнозиро­вания.

Закономерность исследуемого процесса находит отражение в наличии определенных статистических свойств остаточной ком­поненты, а именно: независимости уровней, их случайности, со­ответствия нормальному закону распределения и равенства нулю средней ошибки.

Независимость остаточной компоненты означает отсутствие автокорреляции между остатками (y_i - y_Тi).

Очевидно, важно иметь критерий, позволяющий устанавли­вать наличие автокорреляции. Таким критерием является крите­рий Дарбина — Уотсона, в соответствии с которым вычисляется статистика d:

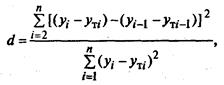
где: y_i; y_i-1 - уровни фактического динамического ряда;

y_Тi, y_{Т i-1} - теоретические (прогнозные) уровни динамического ряда; n - объем выборки.

Возможные значения статистики лежат в интервале 0 < d < 4. Согласно методу Дарбина и Уотсона существует верхний d_в и нижний d_a пределы значимости статистики d. Эти критические значения зависят от уровня значимости α, объема выборки п и числа объясняющих переменных m (для трендовых моделей m=1).

Вычисленное значение d сравнивается с d_в и d_a най­денными по специальным таблицам. При этом руководствуются следующими правилами:

1) d_B < d < 4 — d_B — принимается гипотеза: автокорреляция отсутствует;

2)0<d<d_H — принимается гипотеза о существовании положительной автокорреляции остатков;

3) dH < d < dH и 4 — dB<d<4 — dti

— при выбранном уровне значимости нельзя прийти к определенному выводу;

4) 4 — d_H<d<4 — принимается гипотеза о существовании отрицательной автокорреляции остатков.

Критерий Дарбина — Уотсона имеет два недостатка. Первый из них — наличие области неопределенности, в которой с по­мощью данного критерия нельзя прийти ни к какому решению. Второй — при объеме выборки меньше 15 для d не существует критических значений d_H и d_B. В этом случае для оценки незави­симости уровней ряда можно использовать коэффициент авто­корреляции r _а. Данный показатель приближенно можно вычис­лить по формуле:

где: d - статистика Дарбина - Уотсона.

Расчетное значение r _а сравнивают с табличным. Крити­ческое значение коэффициента автокорреляции r _{а т} имеет одну степень свободы f = п. Если r _а < r _{а т} - уровни динамического ряда независимы.

Контрольные вопросы

1. Какие требования предъявляются к параметрам системы при прогнозировании?

2. Опишите алгоритм прогнозирования.

3. Дайте определение понятию «флуктуация».

4. Что называют временным рядом?

5. Какие этапы целесообразно рассматривать при анализе временного ряда?

6. Дайте определение понятию «тренд».

7. Сущность прогнозной экстраполяции.

8. Какие виды моделей используются при прогнозировании?

9. Каким образом осуществляется выбор тренда?

10. Охарактеризуйте критерий Дарбина – Уотсона.

Лекция 14

Дата добавления: 2015-10-29