Прогнозная экстраполяция

Прогнозирующая модель, ее характер и общий план составления

Модели, прогнозирующие величины изучаемого технико-экономического показателя, могут быть трех видов:

- однофакторные, выражающие изменения самого показателя;

- парные регрессионные, выражающие изменения показателя в зависимости от изменения одного фактора;

- многофакторные, выражающие изменения показателя в зависимости от группы важнейших, определяющих его факторов.

Модели, с помощью которых прогнозируется изменение только самого показателя, независимо от причин его (показателя) вызывающих, мало эффективны, особенно для оперативного управления. Такие модели не позволяют выявить направление и меру воздействия на определенные факторы для достижения уровня показателя, заданного на прогнозируемый период. Парные регрессионные модели, описывающие зависимость изменения показателя от единственного фактора, не учитывают всю совокупность важнейших факторов, а их взаимодействие может привести к значительным искажениям изолированного влияния учтенного фактора.

Весьма ценными являются многофакторные прогнозирующие модели, охватывающие важнейшие факторы, обусловливающие изменение изучаемого показателя, учитывающие взаимосвязи между ними. При этом особенно важно включение в модель именно управляемых факторов, причем по состоянию на несколько периодов, предшествующих прогнозируемому. По каждому фактору должен быть выявлен лаг, указывающий продолжительность запаздывания наибольшего влияния фактора на показатель. При отсутствии лага по данному фактору следует заменять этот фактор его авторегрессионной моделью. Если, например, всех факторов четыре: факторы х₁ и х₂ — запаздывают с лагами L₁ и L₂, а факторы х₃ и х₄ действуют синхронно, то многофакторную модель следует строить в виде:

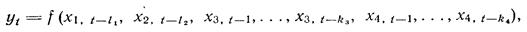
На основании изучения статистических данных и логическо­го анализа протекания изучаемого процесса из заданного масси­ва функций отбираются наиболее приемлемые виды уравнений связи. Этот этап необходим, так как позволяет при отборе функ­ций учесть основные условия протекания рассматриваемого про­цесса и требования, предъявляемые к математической модели. На этом этапе должны быть решены следующие вопросы:

а) является ли исследуемый показатель величиной монотонно возрастающей (убывающей), стабильной, периодической, имеющей один или несколько экстремумов;

б) ограничен ли показатель сверху или снизу каким-либо пределом;

в) имеет ли функция, определяющая процесс, точку перегиба;

г) обладает ли анализируемая функция свойством симметричности;

д) имеет ли процесс четкое ограничение развития во времени.
Наиболее предпочтительно использовать в прогнозной экстраполяции технико-эксплуатационных показателей функции (модели) прогноза, предс­тавленные в таблице.

Окончательное решение о виде аппроксимирующей функции может быть принято после определения ее параметров и верифи­кации прогноза по ретроспективному ряду. Поэтому для прогно­зирования используют несколько подходящих аппроксимирую­щих функций, с тем, чтобы после оценки точности выбрать наи­более подходящую.

На этапе оценки математической модели прогнозирования определяются параметры раз­личных видов аппроксимирующих функций. Наиболее распро­страненными методами оценки параметров аппроксимирующих зависимостей являются метод наименьших квадратов (МНК) и его модификации, метод экспоненциального сглаживания, ме­тод вероятностного моделирования, метод адаптивного сглажи­вания.

Дата добавления: 2015-10-29