Антагонистические игры. Игры с нулевой суммой

Игра называется игрой с нулевой суммой, если в каждой окончательной позиции функция выигрыша (p₁, p₂,..., p_n), где p_i – выигрыш i -го игрока в этой позиции, удовлетворяет условию:

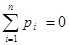
Вообще говоря, игра с нулевой суммой представляет собой замкнутую систему: все то, что кто-нибудь выиграл, должно быть кем-то проиграно.

Игры двух лиц с нулевой суммой называются антагонистическими, или строго конкурентными.

В случаях антагонистической игры можно просто задавать первую компоненту вектора выигрышей, тогда вторая компонента равна первой с противоположным знаком. Т.е. первая компонента называется просто выигрышем, это означает, что второй игрок отдает эту сумму первому.

В антагонистических играх нет никаких оснований для переговоров между игроками, так как если один выигрывает, то другой проигрывает. Этим антагонистические игры отличаются ото всех остальных.

Нормальная форма

Нормальная форма конечной антагонистической игры сводится к некоторой матрице А с числом строк, равным числу стратегий игрока 1 и с числом столбцов, равным числу стратегий игрока 2:

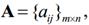
где: а_ij – величина выигрыша, если 1-й игрок выбирает стратегию i, а 2-й -стратегию j;

m – число стратегий первого игрока;

n – второго игрока.

Ситуация (пара стратегий) будет равновесной тогда и только тогда, когда соответствующий ей элемент а_ij является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой.

Теорема о минимаксе

Для любой функции F (x, y), определенной на произвольном декартовом произведении X×Y, имеет место неравенство

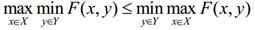
Отсюда следует, что v₁≤v₂.

Нижний выигрыш игрока 1 не может превышать верхнего проигрыша игрока 2.

Теорема о минимаксе утверждает, что v₁≤v₂.

Эта важнейшая теорема доказана многими способами.

Дата добавления: 2015-10-29