Определение местного часового угла и склонения звезды в заданный момент

Часовой угол любой звезды определяется из основной формулы времени (смотри §3.2)

.

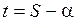Вместо того чтобы вычитать прямое восхождение a светила из звездного времени S, удобнее прибавлять его звездное дополнение

.

Часовой угол звезды на гринвичском меридиане определяется формулой

.

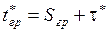Чтобы получить местный часовой угол на заданном меридиане, необходимо к левой и правой частям выше указанного выражения необходимо прибавить долготу места l

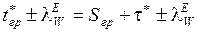
получаем

.

Таким образом, для определения местного часового угла звезды необходимо:

1. Для заданного момента наблюдений рассчитать всемирное время Т_гр и дату.

2. Из ежедневных таблиц выбирать звездное гринвичское время S_т (гринвичский часовой угол точки Овна) на табличный момент всемирного времени.

3. Из основной интерполяционной таблицы, соответствующей минутам всемирного времени Т_гр для заданного момента, в столбце «Точка овна» найти полное изменение D S за минуты и секунды Т_гр.

4. Сложить величины S_т и D S, получим значение звездного гринвичского времени S_гр для заданного момента.

5. Из таблицы «Звезды. Видимые места» простым интерполированием выбрать для заданной звезды звездное дополнение 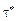и склонение d.

6. Сложить величины S_гр и , получаем гринвичский часовой угол звезды 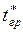, который при помощи долготы перевести в местный часовой угол .

Пример 4.1. Определить местный часовой угол и склонение звезды a Скорпиона (Антарес) 14.V.2002 г. Т_с = 23^h15^m в долготе l = 150°12,4¢ W в момент времени по хронометру Т_хр = 9^h10^m56^s, поправка хронометра u = + 4^m12^s.

Решение.

1) Рассчитываем приближенное гринвичское время Т_гр и дату на момент наблюдений.

14.V Тс	23^h15^m
NW
15.V Тгр	9^h15^m

2) Рассчитываем местный часовой угол и склонение d^* звезды a Скорпиона (Антарес).

срТхр	9^h10^m56^s
uхр	+4^m12^s
15.V Тгр	9^h15^m08^s
Sт	142°09,2¢
D S	9°00,5¢
Sгр	129°18,6¢
l	3°47,6¢
Sм	133°06,2¢
	112°36,7¢
	245°42,9¢ W
	114°17,1¢ E
d^*	26°26,2¢ S

Ответ: = 114°17,1¢ E, d^*= 26°26,2¢ S

Определение местного часового угла и склонения Солнца,
планеты и Луны на заданный момент

1. По гринвичской дате и табличному моменту всемирного времени, ближайшему меньшему к Т_гр наблюдений, из ежедневных таблиц выбирают t_т и d _т Солнца, планеты или Луны. Одновременно выбирают величину и знак квазиразности и разности D. Для Солнца и планет и D приведены в нижней части левой страницы разворота на трехсуточный интервал, для Луны – справа от столбцов t_т и d _т этого светила.

2. Из основных интерполяционных таблиц в столбце «Солнце и планеты» или «Луна» находят основное изменение D₁ t к часовому углу за минуты и секунды Т_гр.

3. Из этой же интерполяционной таблицы из столбцов «Попр.» по аргументу квазиразности находят дополнительное изменение D₂ t к часовому углу (всегда положительное), а по аргументу разности D – поправку Dd к склонению. Знак Dd соответствует знаку D.

4. Складывают величины t_т, D₁ t и D₂ t, а также d _т и Dd и получают гринвичский часовой угол t_гр и склонение d светила на заданный момент Т_гр. Величину t_гр переводят в t_м, пользуясь долготой наблюдателя. Если t_м оказывается больше 180°, переводят его в восточный.

Пример 4.2. 13.IX.2002 г. Т_с = 10^h41^m в долготе l = 59°24,5¢ E в момент времени по хронометру срТ_хр = 6^h32^m15^s, поправка хронометра u = + 8^m42^s. Определить и 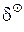Солнца.

Решение.

1) Рассчитываем приближенное гринвичское время Т_гр и дату на момент наблюдений.

13.IX Тс	10^h41^m
NE
13.IX Тгр	6^h41^m

2) Рассчитываем и .

срТхр	6^h32^m15^s
uхр	+8^m42^s
13.IX Тгр	6^h40^m57^s
	270°59,0¢
	10°13,6¢
	0,8¢
	281°13,4¢
l E	59°24,5¢
	340°37,9¢ W
	19°22,1¢ E
	3°50,9¢ N
	– 0,7¢
	3°50,2¢ N

Ответ: = 19°22,1¢ E; = 3°50,2¢ N.

Дата добавления: 2015-10-29