Земная рефракция. 1 страница

Наклонение видимого горизонта

Предположим, что точка А представляет глаз наблюдателя, находящийся на высоте АМ = е (рис. 5.9) над уровнем моря, ОА – отвесная линия наблюдателя и АВ – истинный горизонт наблю­дателя. Если из т. А провести прямые Аn, Ар, Аq, Аn ¢ и т.д. касательные к поверхности Земли, то геометрическое место точек касания представит малый круг npqn ¢ с полюсом в точке М. Этот круг и представлял бы собой линию видимого горизонта наблюдателя. Однако, Земля, как известно, обладает атмосферой, плотность которой в нижних слоях наиболее высокая. Вследствие этого линией горизонта будет не малый круг nn ¢, а малый круг NN ¢ с несколько большим сферическим радиусом. Благодаря преломлению лучей в атмосфере, луч из точки N к глазу наблюдателя пойдет не по прямой линии, а по кривой NA, и наблюдатель увидит точку горизонта N по направлению касательной к этой кривой, т.е. по направлению AF.

Угол nAN между действительным и видимым направлением на горизонт называется земной рефракцией r.

Угол HAF между плоскостью истинного горизонта и направлением на видимый горизонт называется наклонением видимого горизонта d.

Значение d зависит от высоты глаза наблюдателя. Для среднего значения коэффициента земной рефракции значение d может быть получено из выражения:

.

На величину наклонения видимого горизонта оказывает влияние состав атмосферы, температура воды и другие гидрометеорологические условия. Эти факторы влияют на коэффициент земной рефракции. Чтобы повысить точность измерения высот светил рекомендуется определять действительное значение d при фактических условиях наблюдений при помощи наклономера – прибор для измерения наклонения видимого горизонта.

Полученное значение d необходимо вычесть из измеренной высоты h ¢ и исправленная таким образом высота называется видимой высотой h_В.

.

Астрономическая рефракция

Плотность Земной атмосферы уменьшается с высотой, в результате этого идущий от светила луч света распространяется в атмосфере не прямолинейно, а по некоторой кривой линии (рис. 5.10). По мере приближения к Земле усиливается преломления светового луча. Наблюдатель видит светило С ¢ по касательной к приходящему лучу, как бы приподнятое по отношению к истинному положению светила С. Рассматриваемое явление преломления лучей называется астрономической рефракцией. Угол r между истинным и видимым направлением на светило так же называется астрономической рефракцией.

Вычитая поправку за астрономическую рефракцию из видимой высоты h_В получаем топоцентрическую h_тц высоту светила

h_тц = h_В – D h_р.

Величина астрономической рефракции зависит от высоты светила. Наибольшую рефракцию имеют светила расположенные у горизонта. Рефракция также зависит от атмосферного давления и температуры воздуха, поэтому вводят дополнительные поправки за давление D h_В и за температуру D h_t.

Параллаксы светил

Высоты светил, измеренные из разных точек на поверхности Земли, должны быть приведены к центру Земли. Для этого в результате наблюдений вводят поправку за суточный параллакс светила D h_p.

Суточным параллаксом называется угол p ₀ при центре светила, под которым был бы виден со светила радиус Земли. Наибольший параллакс наблюдается при нахождении светила на горизонте. На рис. 5.11 видно, что для приведения высоты к центру Земли значение параллакса всегда прибавляется:

h = h_тц + D h_p,

где h – истинная высота светила.

Полудиаметры светила

При наблюдениях Солнца и Луны получают высоты верхнего или нижнего края диска светил. Для определения высоты центра светила необходимо учитывать со своим знаком величину его углового радиуса R или полудиаметра. Значения R Солнца и Луны приведены в ежедневных таблицах МАЕ.

Исправление высот светил, измеренных над линией
видимого горизонта

Для получения истинной высоты светила необходимо исправить отсчет секстана всеми поправками:

.

Значения поправок приведены в МТ-75, Вас-58, ТВА-57, а также в МАЕ. Некоторые поправки в МТ-75 объеденины в общие поправки.

Пример 5.1. 5.X.2002г. измерена высота звезды = = 18°22,3¢; і = – 2,2¢; s = + 0,1¢; e = 5,2 м; t = + 15°C; В = 775 мм. рт. ст. Определить обсервованную высоту звезды.

Решение.

МТ-75		МАЕ, 2002
	18°22,3¢				18°22,3¢
i + s	– 2,1¢			i + s	– 2,1¢
h¢	18°20,2¢			h¢	18°20,2¢
d	– 4,0¢	(табл. 11-а)		d	– 4,0¢
	18°16,2¢				18°16,2¢
	– 2,9¢	(табл. 9-а)			– 2,9¢
D ht	0,0¢	(табл. 14-а)		D ht	0,0¢
D hB	0,0¢	(табл. 14-б)		D hB	– 0,1¢
	18°13,3¢				18°13,2¢

Пример 5.2. 15.IX.2002г. измерена высота планеты Венеры 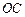= 22°13,5¢; і = + 1,2¢; s = – 0,3¢; e = 7,2 м; t = + 20°C; В = 765 мм. рт. ст. Определить обсервованную высоту планеты Венера.(Для наблюдений Венеры днем вводят поправку D h _ф, которая выбирается из МАЕ)

Решение.

Аргументами таблицы 9-б МТ-75 являются топоцентрическая высота светила h_тц и горизонтальный экваториальный параллакс р ₀ определяемый по МАЕ.

МТ-75		МАЕ, 2002
	22°13,5¢				22°13,5¢
i + s	+ 0,9¢			i + s	+ 0,9¢
h¢	22°14,4¢			h¢	22°14,4¢
d	– 4,7¢	(табл. 11-а)		d	– 4,7¢
	22°09,7¢				22°09,7¢
	– 2,4¢	(табл. 9-а)			– 2,4¢
hтц	22°05,3¢			hтц	22°05,3¢
	+ 0,3¢	(табл. 9-б)			+ 0,3¢
D ht	+ 0,1¢	(табл. 14-а)		D ht	+ 0,1¢
D hB	0,0¢	(табл. 14-б)		D hB	0,0¢
	22°05,7¢				22°05,7¢

Пример 5.3. 1.XI.2002 г. измерена высота нижнего края Солнца = 46°10,3¢; і = – 1,2¢; s = – 0,1¢; e = 12,2 м; t = + 20°C; В = 765 мм. рт. ст. Определить обсервованную высоту Солнца.

Решение.

МТ-75		МАЕ, 2002
	46°10,3¢				46°10,3¢
i + s	– 1,3¢			i + s	– 1,3¢
h¢	46°09,0¢			h¢	46°09,0¢
d	– 6,2	(табл. 11-а)		d	– 6,2¢
	46°02,8¢				46°02,8¢
	+ 15,3¢	(табл. 8)			– 0,8¢
D ht	0,0¢	(табл. 14-а)		R	+ 16,1¢
D hB	0,0¢	(табл. 14-б)		D ht	0,0¢
	46°18,1¢			D hB	0,0¢
					46°18,1¢

Пример 5.4. 22.IX.2002 г. Т_гр = 12^h05^mизмерена высота нижнего края Луны = 23°54,6¢; і = – 2,2¢; s = + 0,3; e = 6,2 м; t = + 10°C; В = 775 мм. рт. ст. Определить обсервованную высоту Луны.

Решение.

Горизонтальный экваториальный параллакс Луны определяется по МАЕ на заданное гринвичское время.

МТ-75		МАЕ, 2002
	23°54,6¢				23°54,6¢
i + s	– 1,9¢			i + s	– 1,9¢
h¢	23°52,7¢			h¢	23°52,7¢
d	– 4,4¢	(табл. 11-а)		d	– 4,4¢
	23°48,3¢				23°48,3¢
	+ 61,8¢	(табл. 10)			+ 60,2¢
D ht	0,0¢	(табл. 14-а)			+ 2,6¢
D hB	0,0¢	(табл. 14-б)			+ 0,1¢
	24°55,1¢			D ht	0,0¢
				D hB	– 0,1¢
					24°55,1¢

Исправление высот светил, измеренных над береговой чертой

Если линия видимого горизонта под светилом закрыта берегом, то высоту светила надо измерять над урезом воды у береговой черты.

Схема исправления высот светил измеренных над береговой чертой такая же как и в случае исправление высот светил, измеренных над линией видимого горизонта.

Наклонение горизонта, ограниченного препятствием определяют по формуле

,

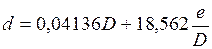где е – высота глаза наблюдателя в м, D – расстояние до препятствия в азимуте светила в кб.

По выше приведенной формуле составлена таблица 11-б МТ-75. Аргументами этой таблицы является высота глаза наблюдателя и расстояние до препятствия.

Пример 5.5. 5.VI.2002 г. измерена высота нижнего края Солнца 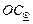= 44°17,8¢; і = – 1,5¢; s = + 0,2¢; e = 12 м; D = 18 кб t = + 20°C; В = 765 мм. рт. ст. Определить обсервованную высоту Солнца.

Решение.

МТ-75
	44°17,8¢
i + s	– 1,3¢
h¢	44°16,5¢
d	– 13,1¢	(табл. 11-б)
	44°03,4¢
	+ 15,0¢	(табл. 8)
	44°18,4¢

Исправление высот светил, измеренных
в искусственный горизонт

Если видимый горизонт закрыт, то высоту светила можно измерить в искусственный горизонт. Искусственный горизонт представляет собой плоский сосуд, наполненный жидкостью (машинное масло, натуральная нефть).

Исправление высот светил, измеренных в искусственный горизонт, имеет две особенности:

1. При измерении высоты в искусственный горизонт с секстана снимают двойной отсчет высоты светила над истинным горизонтом. Исправляя этот отсчет поправкой индекса секстана i и инструментальной поправкой секстана s, и разделив затем пополам, получаем видимую высоту светила.

2. При измерении высоты в искусственный горизонт нет надобности исправлять полученный результат наклонением видимого горизонта d, так как в этом случае высота измеряется над истинным горизонтом.

Приводимые особенности позволяю получать обсервованную высоту с более высокой точностью, чем при наблюдениях над линией видимого горизонта.

Исправление высот светил в этом случае выполняют по следующей схеме

Пример 5.6. 15.V.2002 г. измерена высота нижнего края Солнца = 88°10,3¢; і = – 1,2¢; s = – 0,1¢; t = + 25°C; В = 765 мм. рт. ст. Определить обсервованную высоту Солнца.

Решение.

МТ-75		МАЕ, 2002
	88°10,3¢				88°10,3¢
i + s	– 1,3¢			i + s	– 1,3¢
	88°09,0¢				88°09,0¢
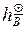
	44°04,5¢				44°04,5¢
	+ 15,0¢	(табл. 8)			– 0,9¢
D ht	+ 0,1¢	(табл. 14-а)		R 	+ 16,0¢
D hB	0,0¢	(табл. 14-б)		D ht	+ 0,1¢
	44°19,6¢			D hB	0,0¢
					44°19,7¢

§5.7. Приведение светил к одному моменту и зениту

Почти все задачи мореходной астрономии требуют для своего решения измерения высот, то каждому наблюдателя ценно знать ту точность, с которой измеряются им высоты того или иного светила.

Однако вопрос этот для морских наблюдений на движущемся судне решается не так просто. Как определить точность наблюдений из многократных измерений одной и той же величины известно. Но высота светила непрерывно изменяется и измерить несколько раз одну и ту же высоту одного и того же светила совершенно не возможно; измеряя подряд несколько высот светила, все время измеряют различные углы, и по этим данным совершенно нельзя судить об ошибке наблюдений.

Это изменение высот происходит из-за следующих причин:

- вращение сферы, вследствие чего изменяются высоты всех светил;

- перемещение судна по поверхности Земли, вследствие чего изменяется положение истинного горизонта наблюдателя, а следовательно, изменяется и высота;

- изменения склонения наблюдаемого светила;

- случайные ошибки наблюдения;

Заметим, что систематические (постоянные) ошибки не окажут влияние на изменения высот; под их влиянием все измеренные подряд высоты могут оказаться неверными в одну и ту же сторону и на одну и ту же величину.

Если из измеренных подряд высот исключить влияния вращение сферы, перемещение судна на поверхности Земли, и изменения склонения, – то только тогда можно говорить, что полученные после этого высоты представляют как бы одну и ту же высоту, многократно измеренную, и колебания можно будет отнести к действию случайных ошибок.

Поправка высот к данному моменту

Для того чтобы привести высоты к данному моменту, т.е. чтобы исключить влияние вращение сферы, надо каждую высоту исправить поправкой ∆ h, выражающей собой величину изменения высоты за промежуток времени от момента ее взятия до того момента, к которому высота приводится. Следовательно, для выполнения этой операции при измерении каждой высоты должен быть замечен момент по часам или хронометру, чтобы иметь возможность рассчитать нужные промежутки времени.

Из формулы для определения изменения высоты (см. §2.4)

.

Если принять ∆ h, в минутах получается

.

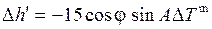Приводить высоты можно к любому моменту, вперед или назад, но при пользовании формулой необходимо помнить, что, приводя предыдущую высоту к последующему моменту, надо величину ∆ h в этой формуле считать положительной при западных, и отрицательных при восточных часовых углах; приводя же последующую высоту предыдущему моменту, указанные знаки ∆ h будут обратные.

Азимут может быть вычислен аналитически (по φ, δ и t), но так как большой точности в определении азимута не требуется, то практически проще, определить азимут светила, взяв его пеленг по компасу вместе с измерением высоты, и исправить его поправкой компаса.

Приведение высот к одному зениту

Если наблюдатель перемещается по поверхности Земли, то соответственно перемещается на сфере его зенит и связанная с ним плоскость истинного горизонта, а следовательно, изменяется высота светила независимо от ее изменения вследствие суточного вращения сферы.

В этом случае для оценки точности измерений высота светила, все измеренные подряд высоты должны быть отнесены к одному и тому же зениту, т.е. должны быть рассчитаны высоты, которые были бы измерены, если бы наблюдатель на Земле не менял своего места.

Для этого в результат наблюдений вносят поправку ∆ h_z, которая учитывает изменение высоты светила вследствие перемещения судна.

Обычно все высоты приводят к зениту последних наблюдений. Поправку ∆ h_z рассчитывают по формуле

,

где S – плавание судна за время между наблюдениями; А – ИК –курсовой угол на светила.

В таблице 16 МТ-75 “Приведение высот к одному зениту” или в таблице МАЕ “Приведение высот к одному месту измерений” приводятся значения изменения высоты за 1 минуту плавания судна ∆ h_v. Следовательно, для определения поправки ∆ h_z необходимо ∆ h_v умножить на промежуток времени между измерениями высот в минутах:

.

Пример 5.7. В j = 46,6° N судно следует ИК = 334,0° со скоростью V = 16 уз. Измерена серия из пяти высот светила, азимут которого А = 84,7° NW. Моменты наблюдений T_i и отсчеты секстана ОС_i:

Ti	ОСi
5^h34^m12^s	33°35,4¢
5^h34^m41^s	33°29,9¢
5^h35^m09^s	33°25,6¢
5^h35^m26^s	33°23,0¢
5^h35^m44^s	33°19,3¢

Определить средний отсчет секстана срОС.

Решение.

1) Вычисляем курсовой угол КУ на светило

КУ = А – ИК

КУ = 275,3° – 334,0° = 301,3°

2) Определяем приведенные отсчеты секстана к одному моменту и к одному зениту

К одному моменту измерения приводятся по формуле

.

К одному зениту измерения приводим по таблице Морского астрономического ежегодника “Приведение высот к одному месту измерений” аргументы которой КУ и V.

Дата добавления: 2015-10-29