
Читайте также:
|
Первая экваториальная система координат отличается от второй только начальным меридианом отсчета. В первой экваториальной системе координат часовой угол отсчитывается от полуденной части небесного меридиана, а во второй – прямое восхождение – от меридиана точки Овна. Положение точки Овна определяется её часовым углом t ^, тогда из рис. 1.7
 .
.
Круговой часовой угол точки овна t ^ равен сумме кругового часового угла t некоторого светила С и прямого восхождения a этого же светила.
§1.5. Графическое решение задач на небесной сфере
При решении конкретных задач применяется более удобная для данного случая система координат. В горизонтной системе координат, ориентированной в пространстве относительно отвесной линии наблюдателя, координаты h и А светила зависят от положения наблюдателя на Земле, поэтому по ним можно определить географические координаты наблюдателя. Часовые углы измеряют угол поворота небесной сферы, поэтому их удобнее применять при измерении времени. Очень часто возникает необходимость переходить от одной системы координат к другой. Самым простым способом перехода от одной системы координат к другой является графическое построение небесной сферы. Для построения небесной сферы необходимо знать широту j, а иногда и долготу l наблюдателя.
Для связи широты наблюдателя с координатами точек небесной сферы удобнее применять плоское изображение небесной сферы. Для получения такого изображения местная сфера проектируется на плоскость меридиана наблюдателя (рис. 1.8). По определению угол между отвесной линией zn и плоскостью небесного экватора равен географической широте наблюдателя, то есть дуга Qz = j. с другой стороны, эта же дуга является склонением точки зенита z. Следовательно, j = d z – склонение точки зенита равно широте места наблюдателя на Земле.
 Из рис. 1.8 видно, что дуга zPN = 90°– j, а дуга NPN = j. С другой стороны дуга NPN является высотой повышенного полюса мира PN. Следовательно,
Из рис. 1.8 видно, что дуга zPN = 90°– j, а дуга NPN = j. С другой стороны дуга NPN является высотой повышенного полюса мира PN. Следовательно,  . Из всего выше изложенного получается следующая зависимость
. Из всего выше изложенного получается следующая зависимость
 .
.
Высота повышенного полюса мира, или склонение точки зенита, равны широте места наблюдателя.
 Графическое преобразование координат на небесной сфере
Графическое преобразование координат на небесной сфере
Переход от одной системы координат к другой можно осуществить несколькими способами, но наиболее простой – это построение небесной сферы и систем координат от руки.
Построением небесной сферы называется выполнение перспективного или плоского рисунка её с нанесением основных плоскостей, линий, точек и систем координат. Удобнее применять перспективное изображение местной небесной сферы (рис. 1.2).
Меридиан наблюдателя проводится циркулем, а остальные кривые наносятся от руки.
Правила построения небесной сферы:
- все большие круги, кроме меридиана наблюдателя, изображаются эллипсами;
- линии, расположенные внутри сферы или не её обратной стороне, изображаются пунктирами;
- дуги, равные координатам, откладываются на глаз, приблизительно в масштабе основной окружности с точностью до ± 5°, от центра чертежа к его краям.
пример 1. 1. Построить небесную сферу для наблюдателя, находящегося в j = 30° S и наблюдающего светило с координатами d = 10° S и t = 50° W. Определить высоту светила h и азимут А.
Решение.
Строим небесную сферу для j = 30° S (рис. 1.9).
От точки Q по небесному экватору в сторону W откладываем дугу, равную часовому углу светила, то есть 50°.Через полученную точку В проводим круг склонения светила и на нем от точки В в сторону PS откладываем дугу равную 10°. Полученная точка С и будет являться светилом. Проводим через точку С вертикал и по нему от плоскости истинного горизонта до светила, на глаз, определяем высоту светила h» 35°. По дуге истинного горизонта определяем азимут светила С:
Ач» 85° NW; Апол» 95° SW; Акр» 175°.
§1.6. Элементы сферической тригонометрии
 Сферическим треугольником называется геометрическая фигуру АВС на поверхности сферы, образованная тремя дугами больших кругов, проходящих через три точки сферы, называемые вершинами этого треугольника (рис. 1.10). Дуги больших кругов, соединяющие вершины сферического треугольника называются его сторонами, а сферические углы, образуемые сторонами – углами сферического треугольника.
Сферическим треугольником называется геометрическая фигуру АВС на поверхности сферы, образованная тремя дугами больших кругов, проходящих через три точки сферы, называемые вершинами этого треугольника (рис. 1.10). Дуги больших кругов, соединяющие вершины сферического треугольника называются его сторонами, а сферические углы, образуемые сторонами – углами сферического треугольника.
Каждая из сторон и каждый из углов сферического треугольника не может быть больше 180°. Сумма сторон сферического треугольника может находиться в пределах от 0 до 360°, а сумма углов – от 0 до 540°.
Для выведения необходимых соотношений из вершины А сферического треугольника АВС опустим на плоскость ВСО (точка О является центром сферы) перпендикуляр АК (рис. 1.11). Из точки К лежащей в плоскости ВСО, опустим перпендикуляры КМ и KL на радиусы сферы ОС и ОВ. Проведём отрезки АМ и АL. Построим отрезок LF, параллельный отрезку КМ, и отрезок KG, параллельный отрезку MF. При таком построении получается шесть прямоугольных плоских треугольников:
D АМО, D АLО, D LОF, D LGK, D ALK, и D AMK. 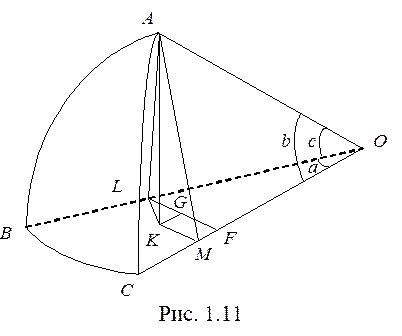
Определим длину отрезка АК из треугольников ALK и AMK

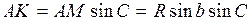
Приравнивая между собой правые части этих двух уравнений, и преобразуя их, получаем формулу синусов
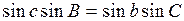 .
.
Опустив перпендикуляр из вершины С на плоскость ВОА или из вершины В на плоскость СОА получили бы формулы синусов в следующем виде:
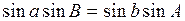 .
.

Запишем очевидное равенство:
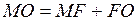
Выразим отрезки MO, MF и FO из треугольников D АМО, D LОF, D АLО, D LGK и D ALK:
 ,
,
 ,
,
 .
.
Откуда получаем
 .
.
Полученная формула называется формула косинуса стороны. По аналогии получаем формулы косинуса для сторон а и с.
 ,
,
 .
.
Запишем ещё одно очевидное равенство
 .
.
Так как
 ,
,
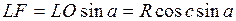 ,
,
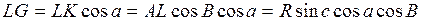 ,
,
получаем формулу, которая называется формулой пяти элементов
 .
.
Аналогично
 ,
,
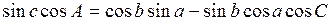 .
.
Выражая из формулы синусов sin b и подставляя его в формулу пяти элементов, получаем формулу четырёх рядом лежащих элементов сферического треугольника
 .
.
Аналогично
 .
.
 ,
,
Приведенные выше формулы сферической тригонометрии значительно упрощаются, если один из углов равен 90°.
§1.7. Параллактический треугольник.
Преобразование координат
Параллактическим (полярным) треугольником называется сферический треугольник PN zC, имеющий вершины в повышенном полюсе, зените и месте светила, и связывающий между собой основные системы сферических координат (рис. 1.13). Угол zСPN называется параллактическим углом q полярного треугольника.
Для решения параллактического треугольника PN zC должно быть известно три его элемента. На практике, для решения задач мореходной астрономии двумя из известных элементов полярного треугольника бывают широта места j, и склонение светила d, а третьим элементом служит часовой угол t или высота светила h.
Элементы полярного треугольника всегда берутся в пределах от 0 до 180°; следовательно, треугольник располагается только на одной половине сферы – на восточной или на западной.

Для определения высоты светила h, если известны j, dи t, применяют формулу косинуса стороны к стороне zC
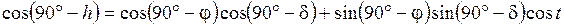 .
.
Откуда получаем
 .
.
Для вычисления азимута А воспользуемся формулой синусов, считая что высота светила h уже известна
 .
.
Упростив это выражение, окончательно получаем

Полученные выше уравнения дают первую систему формул для вычисления высоты h и азимута А светила

Формула sin h является нелогарифмической. При вычислении h с помощью логарифмов тригонометрических функций логарифмы каждого из членов правой части необходимо исследовать на знаки, чтобы выяснить, представляет ли собою правая часть формулы сумму или разность двух слагаемых, в зависимости от чего следует пользоваться вспомогательными логарифмами для сумм или разностей.
Исследования формул на знаки
1. Все функции j являются положительными, так как j не может быть больше 90°.
2. Все функции d, если они одноимённы с j, также являются положительными, так как в этом случае аргумент лежит в первой четверти; если d разноимённо с j то аргумент лежит в четвёртой четверти и все функции, за исключением cosd и secd, считаются отрицательными.
3. В формулы всегда подставляют практический часовой угол светила, величина которого лежит в пределах от 0 до 180°; если t < 90°, то все его функции будут положительными; если t > 90°, то sin t и cosec t будут положительными, а остальные функции – отрицательными.
В результате вычислений азимута по формуле sin А получаем азимут в четвертном счёте. Для определения четверти горизонта необходимо применять правила указанные в таблице 1.1.
Таблица 1.1.
| Наименование d | Величина d | Величина h | Первая буква азимута | Вторая буква азимута | |
| Разноименно с j | Не имеют значения | Разноименно с j | Всегда одноимённо с практическим часовым углом | ||
| Одноименно с j | d > j | h > h I | Разноименно с j | ||
| Одноименно с j | d < j | h < h I | Одноименно с j | ||
| Одноименно с j | d > j | Не имеет значения | Одноименно с j | ||
(h I – высота светила на первом вертикале (таблица 21 МТ-75))
Пример 1.2. Дано j = 46°37,0¢ N, d = 23°26,2¢ N, t = 29°35,1¢ E. Определить h и А.
Решение.


| j = 46°37,0¢ N | sin | 9,86140 | cos | 9,83688 | sec t | 0,26184 | ||||||||
| d = 23°26,2¢ N | sin | 9,59960 | cos | 9,96261 | cos | 9,96261 | ||||||||
| t = 29°35,1¢ E | cos | 9,93933 | sin | 9,69347 | ||||||||||
| I | 9,46100 | II | 9,73882 | sin A | 9,91792 | |||||||||
| арг | 0,27782 | a | 0,18390 | A | 55°52,3¢ SE | |||||||||
| sin h | 9,92272 | Aкр | 124°07,7¢ | |||||||||||
| h | 56°49,4¢ | |||||||||||||
Ответ: h = 56°49,4¢, Aкр = 124°07,7¢
При высотах светила больше 30°, точность вычислений по формулам sin h и sin A снижается, поэтому их заменяют другой более точной функцией  . Перейдя к этой функции и преобразуя формулу sin h заменив в ней
. Перейдя к этой функции и преобразуя формулу sin h заменив в ней  , получаем
, получаем
 .
.
Используя формулу известную из тригонометрии
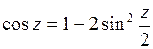
получаем
 .
.
Уравнения  и sin A образуют вторую систему формул для определения высоты h (
и sin A образуют вторую систему формул для определения высоты h ( ) и азимута А светила
) и азимута А светила
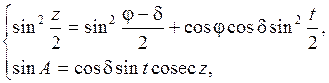
где в формуле для sin A введена замена sec h = cosec z.
Вторая система формул дает более точные результаты и не требует исследования на знаки, так как оба её члена всегда положительны.
Пример 1.3. Дано j = 46°37,0¢ N, d = 23°26,2¢ N, t = 29°35,1¢ E. Определить h и А.
Решение.

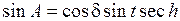
| j = 46°37,0¢ N | cos | 9,83688 | cosec | 0,26184 | ||||||||||||||||||
| d = 23°26,2¢ N | cos | 9,96261 | cos | 9,96261 | ||||||||||||||||||
| t = 29°35,1¢ E | sin2 | 8,81417 | sin | 9,69347 | ||||||||||||||||||
| j – d = 23°10,8¢ | sin2 | 8,60599 | II | 8,61366 | sin A | 9,91831 | ||||||||||||||||
| арг | 0,00767 | a | 0,29705 | A | 55°56,9¢ SE | |||||||||||||||||
| sin2 | 8,91071 | Aкр | 124°03,1¢ | |||||||||||||||||||
| z | 33°09,4¢ | |||||||||||||||||||||
| h | 56°50,6¢ | |||||||||||||||||||||
Ответ: h = 56°50,6¢, Aкр = 124°03,1¢
Азимут светила так же можно получить применив формулу для четырёх рядом лежащих элементов к углу А

откуда получаем
 .
.
Формулу ctg A, является не логарифмической и её необходимо исследовать на знаки, однако она не требует предварительного вычисления высоты светила h.
Вычисленный по формуле ctg A азимут получается в полукруговом счёте. Первая буква в наименовании полукругового азимута одноимённа с широтой, а вторая – с наименованием практического часового угла.
Пример 1.4. Дано j = 46°37,0¢ N, d = 23°26,2¢ N, t = 29°35,1¢ E. Определить А.
Решение.

| j = 46°37,0¢ N | cos | 9,83688 | sin | 9,83688 | ||||||
| d = 23°26,2¢ N | tg | 9,63699 | ||||||||
| t = 29°35,1¢ E | cosec | 0,30653 | ctg | 9,91831 | ||||||
| I | 8,60599 | – II | 8,61366 | |||||||
| арг | 0б32686 | b | 9,72339 | |||||||
| – ctg | 9,83065 | |||||||||
| – А | 55°53,9¢ | |||||||||
| 180°– А | 124°02,1¢ NE | |||||||||
Ответ: Aкр = 124°02,1¢
 Формулы sin h и
Формулы sin h и  состоят из двух слагаемых, т. е. они нелогарифмические и требуют специальных таблиц для сумм a и разностей b. Существует система формул, применение которой выгодно при любом значении высоты h светила над горизонтом, кроме того, данная система формул является логарифмической.
состоят из двух слагаемых, т. е. они нелогарифмические и требуют специальных таблиц для сумм a и разностей b. Существует система формул, применение которой выгодно при любом значении высоты h светила над горизонтом, кроме того, данная система формул является логарифмической.
Из места светила С (рис. 1.14) опускают на меридиан наблюдателя сферический перпендикуляр СD = р, который всегда проходит через точки востока Е и запада W, так как они являются полюсами меридиана наблюдателя.
Обозначим через х расстояние от экватора до основания перпендикуляра, тогда полярное расстояние точки D равно PND = 90° – x, а расстояние 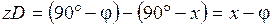 – зенитное расстояние точки D.
– зенитное расстояние точки D.
Получаем два прямоугольных сферических треугольника zDС и PNDС. высоту h и азимут A получаем путем последовательного решения этих треугольников по формулам для четырех рядом лежащих элементов.
Рассмотрим треугольник PNDС в котором d и t известны, а угол D = 90°. Применяя формулу для четырех рядом лежащих элементов, получаем
 ,
,
откуда
 .
.
Из треугольника PNDС определим величину перпендикуляра р через найденное значение х, применяя формулу для четырех рядом лежащих элементов к углу t
 ,
,
откуда
 .
.
Рассмотрим второй прямоугольный сферический треугольник zDС, в котором р и х – р известны, а угол D = 90°. Применяя формулу для четырех рядом лежащих элементов, получаем
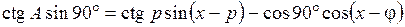 ,
,
откуда
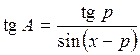 .
.
Применяя формулу четырех рядом лежащих элементов к углу D, получаем
 ,
,
откуда
 .
.
Преобразуя полученные формулы для A, h, р и х, и обозначив величину 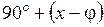 через у, получаем
через у, получаем

На основании этих формул были разработаны профессором Ющенко таблицы высот и азимутов светил (ТВА-57).
§1.8. Специальные таблицы
для расчета высоты и азимута светил
Для определения места судна необходимо знать счислимые высоты и азимуты светил. Счислимыми высотами и азимутами называются те высоты и азимуты которые получены в результате расчетов по счислимому месту судна снятому с карты. Обсервованными высотами называются те которые получены в ходе наблюдений за светилами при помощи угломерного инструмента – секстана. Для определения счислимых высот и азимутов были разработаны специальные таблицы, которые можно подразделить на три группы.
К первой группе таблиц относятся тригонометрические таблицы. В основе этих таблиц лежит разбиение параллактического треугольника на два прямоугольных и решение его по простым формулам сферической тригонометрии (формулы приведены в §1.7).
Примером таких таблиц могут быть таблицы ТВА-57. В этих таблицах используется две тригонометрические функции: тангенс и секанс. Для избежания умножения и деления используют логарифмы тангенса и секанса, а чтобы перейти к вычислениям только с целыми числами, логарифмы увеличены в 20000 раз. В ТВА-57 введены следующие обозначения:  .
.
Правила пользования таблицами ТВА-57, определения знаков и наименований приводятся в описании таблиц.
Пример 1.5. Дано j = 46°37,0¢ N, d = 23°26,2¢ N, t = 29°35,1¢ E. Определить h и А.
Решение.
| d = 46°37,0¢ N | +T (d) | |||||
| t = 29°35,1¢ E | S (t) | –T (t) | ||||
| x = 26°29,6¢ N | T (x) | S (x) | ||||
| j = 46°37,0¢ N | +T (p) | |||||
| y = 90°+(j – x) = 110°07,4¢ | S (y) | –T (y) | ||||
| Ac = 55°53,9¢ SE | T (A) | S (A) | ||||
| hc = 56°50,4¢ | T (h) |
Ответ: hc = 56°50,4¢, Ac = 55°53,9¢ SE = 124°06,1¢
Ко второй группе таблиц относятся таблицы готовых ответов. В этих таблицах для целочисленных значений аргументов j, d и t рассчитаны высоты и азимуты и сведены в таблицы. Интерполяция за минуты производится на основании разложения высоты и азимута в ряд Тейлора с удерживанием первых, а иногда и вторых, членов разложения. для получения результата необходимо произвести следующие действия

Из таблиц готовых ответов на судах наиболее распространены таблицы изданные в СССР ВАС-58, в США НО-214, в Англии НD-486.
Схемы вычисления, правила пользования таблицами, определения знаков и наименований приводятся в пояснениях к таблицам.
Пример 1.6. Дано j = 46°37,0¢ N, d = 23°26,2¢ N, t = 29°35,1¢ E. Определить h и А.
Решение. (По таблицам ВАС-58)
| Арг | Дано | Табл. | разность | h т | 56°02,5¢ | A т | 124,5° | |
| j d t | 46°37,0¢ N 23°26,2¢ N 29°35,1¢ E | 47° 23° 30° | – 23,0¢ + 26,2¢ – 24,9¢ | D h j D h d D ht | + 12,4¢ + 20,6¢ + 15,3¢ | D A j D A d D At | – 0,3° – 0,5° + 0,5° | |
| q | 38° | D h ¶ | – 0,2 | SD А | – 0,3° | |||
| j и d одноименные | SD h | + 48,1 | Ас | 124,2° NE | ||||
| hс | 56°50,6¢ | |||||||
Ответ: hс = 56°50,6¢, Ас = 124,2° NE
Третья группа таблиц относится к, так называемым, искусственным таблицам. Все вычисления в этих таблицах производятся с целыми числами. Порядок определения знаков и наименования азимута указываются в самих таблицах.
Такими таблицами являются таблицы, изданные в СССР «Высоты и азимуты в три минуты» и таблицы «sight reduction table», помещенные в «the nautical almanac».
В настоящее время для расчетов счислимых высоты и азимута широко используют калькулятор и ЭВМ.
При помощи калькулятора h и А вычисляют по следующим формулам
 .
.
Формулу cos h получаем преобразованием формулы sin А из первой системы формул для вычисления высоты и азимута светила. Формулу же tg A получаем преобразованием формулы ctg A.
Выражение для tg A является нелогарифмическим поэтому его необходимо исследовать на знаки (правила исследования на знаки в §1.7).
Если в результате вычислений по формуле tg A полученный результат оказывается отрицательным, то его значение вычитают из 180°, а полученная разность будет являться значением азимута. Вычисленный по формуле tg A азимут получается в полукруговом счете. Наименование азимуту присваивают следующим образом: первая буква в наименовании азимута совпадает с наименованием широты, вторая – с наименованием часового угла.
Пример 1.7. Дано j = 46°37,0¢ N, d = 23°26,2¢ N, t = 29°35,1¢ E. Определить h и А.
Решение.



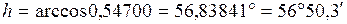
Ответ: hс = 56°50,3¢, Ас = 124,1° NE
§1.9. Точность вычисления счислимых
высот и азимутов светил
Ошибка в счислимой высоте складывается из ошибок в аргументах, ошибок расчетной формулы и таблицы.
Ошибки в аргументах вызывают в среднем ошибку в высоте порядка ± 0,05¢. Ошибки расчетных формул могут быть охарактеризованы средними квадратичными ошибками (как в большую так и в меньшую стороны) в вычисленных высотах.
Таблица 1.2.
| Способ вычислений | Высоты | ||||||||||||||||||||
| 0° | 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° | ||||||||||||
| lg sin h с МТ-75 | 0,02¢ | 0,02¢ | 0,03¢ | 0,04¢ | 0,05¢ | 0,07¢ | 0,09¢ | 0,14¢ | 0,29¢ | – | |||||||||||
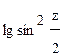 с МТ-75 с МТ-75
| 0,06¢ | 0,05¢ | 0,04¢ | 0,03¢ | 0,03¢ | 0,02¢ | 0,02¢ | 0,01¢ | 0,01¢ | 0,0 | |||||||||||
| ТВА-57 | 0,06¢ | 0,07¢ | 0,10¢ | 0,12¢ | 0,14¢ | 0,14¢ | 0,12¢ | 0,10¢ | 0,07¢ | 0,06¢ | |||||||||||
| ВАС-58 | 0,09¢ | 0,09¢ | 0,09¢ | 0,09¢ | 0,10¢ | 0,11¢ | 0,12¢ | 0,13¢ | – | – | |||||||||||
Точность вычисления азимута по ВАС-58 около ± 0,1°, а по всем остальным таблицам – не ниже ± 0,1¢. Ошибки вычисления вызываются неточностью интерполирования, округлением и другими причинами.
Общая точность счислимой высоты определяемой по таблицам порядка ± 0,1¢–0,2¢.
Глава ІІ.
Видимое суточное движение светил
§2.1. Видимое суточное движение светил.
Явления, связанные с суточным движением светил
Непрерывное перемещение всех светил относительно линий и плоскостей, неразрывно связанных с наблюдателем (отвесная линия, истинный горизонт, меридиан наблюдателя), происходящее вследствие вращения Земли вокруг своей оси, называется суточным движением светил.
Суточное вращение Земли происходит с запада на восток. Однако для наблюдателя находящегося на поверхности Земли удобнее считать, что вращается небесная сфера с востока на запад, а планета остается неподвижной.
В течение суток светило перемещается по своей суточной параллели, которая определяется склонением светила, и проходит ряд характерных точек:
-  точка пересечения суточной параллели светила с восточной частью истинного горизонта называется точкой истинного восхода (точка е на рис. 2.1). Момент пересечения центром светила восточной части истинного горизонта называется моментом истинного восхода;
точка пересечения суточной параллели светила с восточной частью истинного горизонта называется точкой истинного восхода (точка е на рис. 2.1). Момент пересечения центром светила восточной части истинного горизонта называется моментом истинного восхода;
- точка пересечения суточной параллели светила с западной частью истинного горизонта называется точкой истинного захода (точка g на рис. 2.1). Момент пересечения центром светила западной части истинного горизонта называется моментом истинного захода;
- точка пересечения суточной параллели светила с восточной или западной частями первого вертикала называется положением светила на первом вертикале (точка k на
рис. 2.1).
- точка пересечения суточной параллели светила с полуденной частью меридиана наблюдателя называется точкой верхней кульминации (точка d на рис. 2.1). Момент пересечения центром светила полуденной части меридиана наблюдателя называется моментом верхней кульминации;
- точка пересечения суточной параллели светила с частью меридиана наблюдателя называется точкой нижней кульминации (точка f на рис. 2.1). Момент пересечения центром светила полуночной части меридиана наблюдателя называется моментом нижней кульминации.
Дата добавления: 2015-10-29; просмотров: 183 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Горизонтная система координат | | | Наблюдатель находится на полюсе |