Земная рефракция. 2 страница

i	Ti	D Ti		D h ¢	D h z	D h ¢ + D h z	ОСi	прОСi
	5^h34^m12^s	+ 0^m57^s	+ 0,95^m	– 9,7¢	+ 0,1¢	– 9,6¢	33°35,4¢	33°25,8¢
	5^h34^m41^s	+ 0^m28^s	+ 0,47^m	– 4,8¢	+ 0,1¢	– 4,7¢	33°29,9¢	33°25,2¢
	5^h35^m09^s						33°25,6¢	33°25,6¢
	5^h35^m26^s	– 0^m17^s	– 0,28^m	+ 2,9¢	– 0,0¢	+ 2,9¢	33°23,0¢	33°25,9¢
	5^h35^m44^s	– 0^m35^s	– 0,58^m	+ 6,0¢	– 0,1¢	+ 5,9¢	33°19,3¢	33°25,2¢

3) Вычисляем срОС.

,

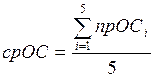Ответ: срОС = 33°25,5¢

Глава VI
Определение места судна в море по небесным светилам

§6.1. Теоретические основы
астрономического определения места судна в море

Задачу эту можно было бы решить чисто аналитически: измерив высоты двух светил заметив при этом моменты и рассчитав гринвичские часовые углы светил, получим два уравнения с двумя неизвестными j и l, которые могут быть найдены при совместном решении этих двух уравнений.

Однако решения этих двух тригонометрических уравнений каждое из которых представляет уравнение соответствующей линии положения на шаре (сфере), достаточно сложно; значительно проще решить задачу иным методом проведением на карте линий положения, точка пересечения которых и даст обсервованное место.

Построим небесную сферу (рис.6.1) так, чтобы ее центр совпадал с центром Земли, и пусть на Земле, в точке а, находится маяк, до которого в некоторый момент времени измерено в милях расстояние, и этим расстоянием проведен малый круг cbd – линия положения на земном глобусе. Положим, что в момент наблюдений в зените этого маяка находится на сфере некоторая звезда А (Z_a); нанесем на сферу зениты точек малого круга c, b, d – точки Z_c, Z_b, Z_d – получим на сфере малый круг Z_cZ_bZ_d, с полюсом в точке А и со сферическим радиусом Z_cA = Z_bA = Z_dA. Этот сферический радиус будет равен сферическому радиусу малого круга cbd; а так как малый круг cbd численно равен измеренному в милях расстоянию ca = ba = da, то и радиус круга Z_c, Z_b, Z_d на сфере, выраженный в дуговой мере, будет также равен этому же расстоянию до маяка, выраженному в милях. С другой стороны, так как все точки на круге Z_cZ_bZ_d являются зенитами соответствующих точек круга cbd, то дуги Z_cA = Z_bA = Z_dA представляют собой зенитные расстояния светила A для наблюдателей на Земле в точках c, b, d; эти зенитные расстояния, а следовательно, и высота светила A у всех наблюдателей на Земле, расположены на малом круге cdb равны между собою. Поэтому этот малый круг на Земле носит название круга равных высот, точка же a – полюса освещения.

Из всего сказанного справедливо и обратное заключение: если известна высота h ₁ какого-либо светила, то стоит только нанести на глобус, представляющий Землю, точку a ₁ – полюс освещения – и из этой точки сферическим радиусом, равным z ₁ = 90°– h ₁, провести малый круг (круг равных высот), – то этот круг и представит линию положения, и верное место судна в момент наблюдений находится где то на этой линии.

Если из того же места на Земле измерена высота h ₂ какого-либо другого светила, надо нанести на Земной глобус второй полюс освещения, провести из этой точки второй круг равных высот радиусом z ₂ = 90°– h ₂ и обсервованное место определится как точка пересечения этих двух кругов равных высот; счислимое место, всегда известное, укажет какую именно из двух точек пересечения надо принимать за обсервованное место.

Для того что бы нанести на глобус какую-либо точку, в данном случае полюс освещения a – необходимо знать ее географические координаты: широту j и долготу l.

Из рис. 6.1 видно, что географическая широта точки a, измеряющаяся дугой qa, равна склонению светила A, измеряющемуся дугой QA, т.е. j _a = d _a.

Проведем Земной и небесный меридиан Гринвича, увидим что долгота точки a, измеряющаяся дугой mq, равна Гринвичскому часовому углу светила A, измеряющемуся дугой MQ, т.е. λ _a = t_грА. Таким образом, нанести на глобус полюс освещения очень просто:

При этом d светила легко выбирается из МАЕ, a t_гра рассчитается по моменту на часах, замеченному при измерении высоты светила.

Таким образам задача определения места решается на земном глобусе графически чрезвычайно просто.

Для того чтобы, осуществляя этот способ на глобусе, получить место с достаточной точностью, надо, чтобы глобус был огромных размеров; так, желая получить на глобусе место с точностью до 0,1¢ морской мили, надо взять глобус диаметром 14 м.

§6.2. Решение задачи определения места судна
методом Сент-Иллера

Для мореплавания особенно ценно было бы решение задачи определения места судна на морской карте, но проведение на ней круга равных высот представляет большое затруднение. Однако, и на глобусе нет смысла проводить полностью круги равных высот достаточно провести лишь небольшие дуги около точки пересечения. При этом с допустимой для практики погрешностью небольшие отрезки кривых могут заменяться касательными к ним прямыми линиями – высотные линии положения.

Наибольшее распространение получил метод построения высотных линий положения, предложений в 1875 году французским моряком Сент-Илером. Сущность методом заключается в следующем: если известны полюс освещения некоторого светила a и счислимое место судна M_c, то можно провести два круга равных высот (рис. 6.2). Один из кругов (h_oh_o) соответствует обсервованной высоте наблюдавшегося светила и описан радиусом (на этом круге располагается обсервованное место судна). Точку К на этом круге, лежащую на кратчайшем расстоянии от М_с, называют определяющей точкой.

Второй круг (h_сh_c) соответствует счислимой высоте того же светила, т.е. высоте, вычисленной по координатам счислимого места M_c. Радиус этого круга .

Угол NМ_oa между меридианом счислимого места и направлением на полюс освящения представляет собой счислимый истинный пеленг полюса освещения ИП_с. Отрезок М_сК, называют переносом и обозначать буквой n. Перенос – расстояние от счислимого места до круга равных высот светила:

.

Проведем в определяющей точки перпендикуляр к линии М_оа, получим отрезок прямой І-І. Этот отрезок и является высотной линией положения наблюдателя.

Из рис. 6.2 следует, что для нанесения на меркатарскую карту высотной линии положения необходимо и достаточно знать счислимый ИП_с полюс освещения а и расстояние М_cK = n по линии пеленга от счислимого места М_с до определяющей точки К. Эти две величины называют элементами высотной линии положения.

Счислимый пеленг ИП_с на полюс освещения численно равен счислимому азимуту А_с наблюдавшегося светила. Поэтому ИП_с может быть получен расчетом А_с из счислимого параллактического треугольника. Из этого же треугольника рассчитывают также значение h_c, необходимое для вычисления переноса n.

Расчет А_с и h производят по формулам сферической тригонометрии (смотри §§1.7, 1.8) или с помощью таблиц ВАС-58, ТВА-57 и. др.

§6.3. Нанесение высотных линий положения
на меркаторскую карту прокладкой от счислимого места

Счислимое место М_с может располагаться вне круга равных высот, внутри круга, а также на самом кругу. В первом случае величина n = h_o – h_c, будет положительной, так как радиус счислимого круга равных высот больше, чем радиус обсервованного круга равных высот. Определяющая точка К по отношению к счислимому месту располагается в направлении к полюсу освещения. Во втором случае величина переноса будет отрицательной и определяющая точка К по отношению к М_с будет располагаться по направлению от полюса освещения. В третьем случае точка К будет совладать с точкой М_с.

Линии положения непосредственно на меркаторской карте прокладываются только в том случае, если карта 1:500000 и крупнее. При плавании в открытом море, где чаще всего приходится пользоваться, астрономическими методами определения места судна, используется генеральные карты. Нанесение на них небольших расстояний, какими являются переносы, оказывается невозможным. В этом случае можно прибегнуть к выполнению прокладки линий положения в желаемом масштабе на листе бумаги, штурманских бланках Ш8 или Ш8б, предварительно задав масштаб.

В практике применяют два способа выбора масштаба для прокладки на листе бумаги:

- линейный;

- угловой.

Рассмотрим применение этих масштабов.

Применение линейного масштаба. Произвольную точку листа бумаги принимают за счислимое место судна М_с, и из этой точки прокладывают линии азимутов (рис. 6.3). В нижней части листа проводят горизонтальную линию, на которой наносят отрезки равной длины, принимаемые за 1¢ боковой рамки карты, т.е. за 1 меркаторсую милю.

С помощью циркуля-измерителя снимают с масштабной линейки, полученные в ходе расчета переносы, и откладывают их по линиям азимутов. Проводят через определяющие точки К ₁ и К ₂ линии положения, получают в их пересечении обсервованное место судна М_о.

Для вычисления обсервованных координат измеряют циркулем РШ точки М_о относительно счислимого места М_с, координаты которого известны, и вычисляютj _o

j _o = j _c + РШ.

Измеренное в том же масштабе расстояние между меридианами счислимого и обсервованного места представит собой отшествие ОТШ этих точек.

С помощью таблицы 25-а МТ-75 по полученному ОТШ и j _o рассчитывают величину РД (или же по формуле ) вычисляют обсервованную долготу l _o

l _o = l _c + РД.

Величину невязки С также снимают с масштабной линейки.

Применение углового масштаба. В нижней части листа проводят горизонтальную линию, а к ней под углом, равным счислимой широте j _c, – наклонную линию (рис. 6.4). На наклонной линии откладывают отрезки равной длины, принимаемые за 1¢ боковой рамки карты. Полученные на наклонной линии точки 1, 2, 3, … проектируют на горизонтальную линию и получают на ней соответствующие точки 1, 2, 3, … в результате проделанной работы будет построен угловой масштаб. Из полученного углового масштаба становится ясно, что минута на прямой линии равна минуте, на наклонной линии умноженной на соsj _c. Таким образом, одно деление на горизонтальной линии соответствует одной экваториальной миле.

Для вычисления координат полученной обсервованной точки измеряют циркулем ее РШ и РД относительно счислимого места. Величину РШ получают с наклонной линии углового масштаба, а РД – с горизонтальной. Величину невязки снимают с наклонной линии.

Угловой масштаб неудобен для прокладки при плавании судна в высоких широтах, где значения соsj уменьшаются очень быстро. Это приводит к резкому уменьшению изображения экваториальной мили на горизонтальной линейке масштаба, а, следовательно, к неточному получению РД и l _o. Кроме того, при построении углового масштаба необходимо брать обсервованную широту. Подмена обсервованной широты счислимой при построении углового масштаба приводит к дополнительной ошибке. Поэтому в широтах больше 60° следует пользоваться только линейным масштабом.

§6.4. Точность обсервации

Прокладкой на карте не заканчивается работа по определению места судна в море. Необходимо провести анализ обсервации т.е. учесть действие предполагаемых случайных и систематических погрешностей на элементы A и n высотной линии положения.

Погрешностью называется разность между истинным значением какой-либо величины и его значением, принятым в расчет.

При проведении на карте или листе бумаги линий азимутов и высотных линий положения в виде прямых линий возникает некоторая погрешность вследствие того, что азимуты и высотные линии положения являются дугами большого и малого кругов. Эта погрешность зависит от величины переноса n и широты места j _c. Если n < 20¢, то погрешность в азимуте и высотной линии положения можно пренебречь.

Перенос n является разностью обсервованной h_о и счислимой высот h_с, поэтому в переносе будут содержатся случайные и систематические погрешность как и в определении счислимой так и в определении обсервованной высоты.

Случайными погрешностями – называются погрешноси причины возникновения, которых неизвестны, а их индивидуальные значения не подчиняются какой-либо закономерности, и в данном ряду наблюдений их величины и знаки могут непрерывно меняться. Свойства этих погрешностей проявляются только при большом числе измерений одной и той же величины, в одинаковых условиях и с одинаковой точностью.

Источниками случайных погрешностей при измерении высот светил могут быть: несовершенство угломерного инструмента, состояние атмосферы (дождь, ветер, температура), состояние горизонта, состояние органов чувств наблюдателя и т.д.

Мерой оценки точности при действии случайных погрешностей является средняя квадратичная погрешность ± m. Вероятность того, что искомая величина будет находится в пределах оцениваемых ± m составляет 68,3%.

Для оценки точности измерений пользуются так называемой предельной средней квадратичной погрешностью, которая равна m_пред = ± 3 m. Вероятность того что искомая величина будет находиться в переделах оцениваемых m_пред составляет 99,7%. Однако в штурманской практике и в соответствии с требованиями ІМО предъявляемыми к точности определения места судна достаточна вероятность 95%, которая определяется как ± 2 m (вероятность 95,4%).

Наиболее просто значение средней квадратичной погрешности может быть определено по методу размаха. Размах R – абсолютная величина разности наибольшего и наименьшего результатов измерений данной серии. Среднюю квадратичную ошибку одного измерения ± m определяется по формуле

,

где k_n – коэффициент, который выбирается из таблицы 6.1 в зависимости от числа измерений в серии N.

Таблица 6.1

N
kn	0,430	0,395	0,370	0,351	0,337	0,325	0,315

Из свойств случайных погрешностей следует, что для уменьшения влияния случайных погрешностей необходимо выполнять серию из 3-5 наблюдений одного и того же светила и результаты осреднять.

Промахи – это грубые погрешности, превышающие по абсолютной величине пределы точности для данного наблюдения, и являются следствием невнимательности и небрежности наблюдателя.

Для выявления промахов прибегают к расчету предельной средней квадратичной погрешности. Если в ряду измерений имеются погрешности превосходящие по своей величине предельные, то они исключаются как промахи.

Пример 6.1. В ходе наблюдений измерения серии высот светила Арктур (a Волопаса) были получены следующие отсчеты секстана ОС, которые затем были приведены к одному моменту: 37°17,8¢; 37°19,2¢; 37°15,4¢; 37°20,1¢; 37°16,7¢; 37°17,7¢; 37°18,7¢. Определить среднюю квадратичную погрешность одного измерения ± m, предельную среднюю квадратичную погрешность m_пред и промахи.

Решение.

Определяем размах R по наибольшему и наименьшему значениям полученных отсчетов секстана

R = 37°20,1¢ – 37°15,4¢ = 4,7¢.

Из таблицы 6.1 определяем k_n по семи измерениям и находим, что

± m = ± 0,370×4,7¢ = ±1,7¢.

Определяем предельную среднюю квадратичную погрешность

m_пред = ± 3×1,7¢ = ± 5,1¢.

Осредняем отсчеты секстана

;

Определяем промахи

срОС ± m_пред

Промахами будем считать значения меньшие, чем 37°12,8¢ и большие чем 37°23,0¢. В измеренной серии высот промахи не содержатся. (Если в наблюдениях содержатся промахи, их исключают из серии и заново определяют все значения.)

Систематические погрешности – погрешности, которые остаются постоянными в данной серии измерений или изменяются по определенному закону при изменении условий наблюдения. К числу систематических погрешностей D относятся поправка индекса секстана i, инструментальная ошибка секстана s и ошибка в определении наклонения видимого горизонта d по таблицам.

Величина и знак погрешности в определении наклонения видимого горизонта для судоводителя неизвестны. D принимать равной от 1 до 3¢ в зависимости от опытности штурмана и погодных условий. В случае применения наклономера систематическую погрешность принимают равной нулю.

В реальных условиях систематические и случайные погрешности действуют всегда совместно, и образуют полную ошибку.

Случайные погрешности в переносе свидетельствуют о наличии рассеивания линии около действительной высотной линии положения. Поэтому действительная высотная линия положения будет находиться где-то рядом с проложенной на карте или плане высотной линией положения, в пределах некоторой полосы положения.

Содержание систематической погрешности смещает полосу положения по линии азимута на расстояние ±D (рис. 6.5).

Оценка точности определения места судна
средней квадратичной погрешностью

При прочих равных условиях точность места судна, полученного по двум высотным линиям положения, зависит главным образом от степени влияния случайных и систематических погрешностей наблюдений и вычислений счислимых высот, т. е. от точности в определении переноса n первой и второй линии положения. средняя квадратичная погрешность линии положения выражается формулой

,

где m_o – средняя квадратическая погрешность обсервованной высоты; m_c – средняя квадратическая погрешность счислимой высоты.

Среднюю квадратическую погрешность обсервованной высоты определяют методом размаха (смотри пример 6.1). Среднюю квадратическую погрешность счислимой высоты определяют по таблице 1.2.

На основании выражений

действию случайных погрешностей наблюденных и счислимых высот подлежат величины D h ₁ и D h ₂, средние квадратические погрешности которых обозначим через m_n, а средние квадратические погрешности широты и отшествия через m _j и m _w.

Так как искомые поправки Dj и Dw выражаются через независимые величины D h ₁ и D h ₂ линейно, то на основании теории случайных ошибок для равноточных наблюдений получаем

Среднюю квадратическую погрешность определения места судна определяют из формулы

,

откуда

.

Из формулы для r видно, что каковы бы ни были азимуты наблюдаемых светил, но при заданной точности наблюдений m_n и разности азимутов (А ₂ – А ₁) сумма квадратов погрешностей широты и отшествия есть величина постоянная. Поэтому, если в одном случае широта определяется точнее, то долгота (отшествие) – хуже и наоборот.

Наиболее точное определение места судна соответствует условиям m _j = m _w. и , которые могут быть выполнены одновременно, если (А ₂ – А ₁) = 90°. В данном случае не зависимо от величины наблюдаемых светил m _j = m _w = m_n и . В этом и состоит преимущество метода линий равных высот, который позволяет определять широту и долготу с наивысшей возможной точностью при наблюдении светил в любых взаимно перпендикулярных азимутах.

Величину r называют радиусом круга погрешности. Определив в пересечении двух высотных линий положения обсервованное место судна М_о, из найденной точки описывают круг погрешности (рис. 6.6), представляющий собой площадь pr², в одной из точек которой находится истинное место с вероятностью этого события 68,3%. Для определения с точностью 95,4% необходимо удвоить радиус круга погрешности:

.

Если разность азимутов наблюдаемых светил не равна 90°, то точность определения места становится в прямую зависимость от азимутов, наблюдаемых светил, причем с уменьшением величины D А очень быстро возрастает радиус круга погрешности r, т.е. увеличивается площадь pr², в которой может находится действительное мести судна.

Влияние систематических постоянных погрешностей
на точность определения места судна

В отличие от случайных погрешностей, действие систематической погрешности состоит в том, что она смещает место судна по направлению среднего азимута на величину D. Вместе с обсервованным местом смещается на ту же величину и круг случайных погрешностей. Поэтому при совместном влиянии случайных и систематических погрешностей истинное место судно в действительности располагается где-то в приделах области ABCD (рис. 6.7).

Влияние на точность определения места судна
погрешностей счисления

При определении места судна по разновременным наблюдениям Солнца (смотри §6.7), кроме указанных погрешностей, оказывают влияние погрешности счисления пути судна, накапливаемые между первыми и вторыми наблюдениями светила.

На точность определения места судна при разновременных наблюдениях будут одновременно оказывать влияния как погрешности в определении истинного курса m_к, так и погрешности в определении пройденного расстояния m_S. Рассчитав обе высотные линии положения и произведя их прокладку из точки М_{с 2} (рис. 6.8), получим место судна в точке М_о. Вследствие действия погрешностей в курсе и плавании счислимая точка М_{с 2} является ошибочной точкой. Очевидно, вторая высотная линия положения II-II, рассчитанная по координатам этой точки, займет на карте правильное положение. Но первую высотную линию положения следовало бы проложить из некоторой другой точки, находящейся внутри круга радиуса r, представляющего собой общую погрешность в курсе и плавании. Под действием этой погрешности первая высотная линия положения может переместиться параллельно самой себе в одно из крайних возможных положений I¢-I¢ или I²-I². Точки пересечения этих линий со второй высотной линией положения М ¢ и М ² представят собой крайние возможные линии положения обсервованного места на линии равных высот II-II. В этом случае погрешность обсервованного выразится отрезком М_оМ ¢ = М_оМ ² = r, определяемым из треугольника М_оМ ¢ С по формуле

.

Из рисунка видно, что

где и , тогда

.

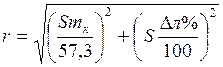Подставляя значение r в выражение для r, получаем

.

Для погрешности в 95% получаем

.

Ошибка r смещает судно по второй высотной линии положения и имеет систематический характер.

Из формулы видно, что величина ошибки прямо пропорциональна плаванию S и обратно пропорциональна , который с увеличением промежутка времени между наблюдениями уменьшается. Практически установлено, что при плавании в средних широтах места судна определяется по Солнцу с наилучшей точностью при разности азимутов 40-50°.

§6.5. Определение места судна в сумерки
по одновременным наблюдениям двух светил

Самое удобное время для наблюдений звезд и планет – период вечерних и утренних навигационных сумерек, когда на небе появляются планеты и значительное количество ярких навигационных звезд. При этом естественный морской горизонт достаточно хорошо виден и доступен для измерения высот светил навигационным секстаном.

Дата добавления: 2015-10-29