Лунные затмения

Земля, освещаемая Солнцем, отбрасывает от себя тень (и полутень) в сторону, противоположную Солнцу (рис. 2.11.). Так как диаметр Солнца больше диаметра Земли, то ее тень имеет форму постепенно суживающегося конуса.

При движении вокруг Земли Луна может попасть в конус земной тени, и тогда произойдет лунное затмение. Лунное затмение возможно только во время полнолуний. Так как, во время затмения Луна лишается солнечного света, то лунное затмение видно на всем ночном полушарии Земли. для всех наблюдателей в этом полушарии лунное затмение начинается в один и тот же момент и заканчивается также одновременно.

Если Луна полностью войдет в земную тень, то произойдет полное затмение Луны, если в тени окажется только часть Луны, то будет наблюдаться частное затмение. Полному или частному затмению предшествует (и завершает их) полутеневое лунное затмение, когда Луна проходит сквозь земную полутень. Полутеневое затмение может быть и без последующего наступления теневого затмения.

§2.9. Прецессия и нутация

Вследствие возмущающего действия Солнца и Луны на вращательное движение Земли, имеющей форму эллипсоида вращения, ось мира и связанный с ней небесный экватор не остаются в пространстве неподвижными, а непрерывно перемещаются в направлении с востока на запад, т.е. ось мира, составляя с осью эклиптики угол 23°26¢, медленно описывает около неподвижной оси эклиптики коническую поверхность. В результате точка Овна ^ будет непрерывно перемещаться по эклиптике навстречу собственному годовому движению Солнца на величину равную 50,3² в год. Полный оборот оси мира вокруг оси эклиптики произойдет через лет.

Прецессией (предварением) равноденствия называется перемещение точки Овна ^ по эклиптике навстречу собственному годовому движению Солнца.

Вследствие прецессионного движения полюса эклиптики перемещаются по небесной сфере, и кривые, описываемые полюсами мира, не замыкаются. В настоящее время северный полюс мира находится вблизи Полярной звезды (a Малой Медведицы), но 4000 лет назад ближе всех к северному полюсу мира была звезда a Дракона, а через 12000 лет «полярной звездой» станет Вега (a Лиры).

Нутация – периодическое колебание земной оси вследствие притяжения Луны. Под влиянием нутации полюса Земли описывают на сфере малый эллипс с полуосями 9 и 7² и периодом полного обращения по эллипсу 18,6 года. Влияние нутации на изменение наклона экватора к эклиптике и перемещение точки Овна настолько незначительно, что при практических расчетах для определения места судна по светилам не принимается во внимание.

Глава III
Измерение времени

§3.1. Основы измерения времени

Вращение Земли вокруг оси происходит почти равномерно, с периодом, равным периоду вращения небесного свода, который достаточно точно может быть определен из наблюдений. Поэтому по углу поворота Земли от некоторого начального положения можно судить о протекшем времени. За начальное положение Земли принимается момент прохождения плоскости земного меридиана места наблюдателя через избранную точку на небосклоне, т.е. момент верхней или нижней кульминации этой точки на данном меридиане.

Основной единицей измерения времени являются сутки. Продолжительность суток зависит от избранной точки на небосклоне. В астрономии за такие точки принимаются:

- точка весеннего равноденствия;

- центр видимого диска Солнца (истинное Солнце);

- «среднее Солнце» – гипотетическая точка небесной сферы, положение которой может быть вычислено теоретически для любого момента времени.

Определяемые этими точками три различные единицы времени называются соответственно

- звездными сутками;

- истинными солнечными сутками;

- средними солнечными сутками,

а время, ими измеряемое, –

- звездными временем;

- истинным солнечным временем;

- средним солнечным временем.

Сутки и их доли (часы, минуты, секунды) используются при измерении коротких промежутков времени.

Для измерения больших промежутков времени служит единица времени, основанная на движении Земли вокруг Солнца, – тропический год. Тропическим годом называется промежуток времени между двумя последовательными прохождениями центра истинного Солнца через точку весеннего равноденствия.

§3.2. Звездные сутки. Звездное время.
Основная формула времени

Для решения задач мореходной астрономии связанных с наблюдениями звезд используют звездное время.

Звездные сутки – промежуток времени между двумя последовательными верхними кульминациями точки Овна. За начало звездных суток принимается момент верхней кульминации точки Овна. Следовательно, звездное время – промежуток времени за который небесная сфера повернулась на некоторый угол от момента верхней кульминации точки Овна. Звездное время – западный часовой угол точки Овна.

Если в данный момент времени известны часовой угол t и прямое восхождение a какого-либо светила С, то звездное время S, из рис. 3.1, будет выражаться следующей формулой

.

Полученное соотношение называется основной формулой времени: звездное время в любой момент равно круговому часовому углу светила плюс прямое восхождение этого же светила.

Если светило будет находится в восточной половине небесной сферы, его круговой часовой угол будет больше часового угла точки Овна то основная формула времени примет следующий вид

,

где 360° – период часового угла, как точки Овна, так и светила.

Основная формула времени связывает звездное время в любой момент с часовым углом светила через прямое восхождение светила – координату независимую от места положения наблюдателя на Земле.

§3.3. Истинные сутки. Истинное время.
Средние сутки. Среднее время

За единицу времени с древних времен были приняты истинные или солнечные сутки. Истинные сутки – промежуток времени между двумя последовательными верхними кульминациями Солнца.

За начало истинных суток принимался момент верхней кульминации Солнца. Истинное время измеряется круговым часовым углом Солнца. Момент верхней кульминации Солнца называется истинным полуднем.

Однако изменение прямого восхождения Солнца неодинаково в течение года, следовательно, и продолжительность истинных суток тоже не одинакова. Разность между самыми длинными и самыми короткими сутками составляет 51 секунду. Применять за единицу счета точного времени переменную величину нельзя.

Чтобы получить постоянную единицу времени, необходимо заменить Солнце, которое неравномерно движется по эклиптике, точкой имеющей равномерное годовое движение. Такая точка получила название среднее Солнце.

Среднее Солнце – гипо­тетическая точка небесной сферы, совершающая равномерное движение по небесному экватору.

Средние сутки – промежуток времени между двумя последовательными нижними кульминациями среднего Солнца. Так как за начало суток применяется момент нижней кульминации среднего Солнца то можно дать следующее определение среднему времени: среднее время измеряется часовым углом среднего Солнца, измененным на 12 часов
(рис. 3.2)

.

Среднее время выражается в часовой мере от 0 до 24 часов, причем моменты среднего времени должны сопровождаться указанием календарной даты, так как календарный счет дней ведется в средних сутках.

Так как за 24 часа часовой угол среднего Солнца изменяется на 360º, можно установить следующее соотношение между выражением углов во временной и градусной (дуговой) мерах:

24 ^h …………. 360º
1 ^h ………….…. 15º	1º ……………. 4 ^m
1 ^m. …………… 15¢	1¢ ……………. 4 ^s
1 ^s ………….…. 15²	0,25¢ ……...…. 1 ^s

Так же для перевода углов из временной меры в дуговую меру и наоборот применяют таблицу 32 МТ-75 или же приложение 4 в «Астрономическом ежегоднике».

§3.4. Местное время. Время на различных меридианах

Вследствие суточного вращения Земли, кульминация одного и того же светила будет происходить раньше на меридианах расположенных к востоку от данного места. Точно так же и сутки будут начинаться раньше на меридианах, лежащих к востоку от данного меридиана.

Следовательно, в один и тот же момент на разных меридианах Земли часы показывают разное время.

Время, определяемое по моменту кульминации среднего Солнца в данном месте, называется местным временем.

Местное время для всех мест, лежащих на одном и том же меридиане, будет одинаково, но в один и тот же момент местное время в данном пункте отличается от местного времени другого пункта на разность долгот, выраженную во временной мере. Причем к востоку времени будет больше, а к западу меньше.

На рис.3.3 дано схематическое изображение звездного времени S, часового угла светила t и среднего времени Т для наблюдателей находящихся на меридиане Гринвича , на восточном меридиане и западном меридиане .

Исходя из рис. 3.3, можно записать следующие выражения для звездного времени S

, ,

или

,

где, S ₁ и S ₂ – местное звездное время S_М в восточном и западном меридианах, а S_гр – звездное время на меридиане Гринвича.

Аналогичным способом получают формулы для часового угла светила и среднего времени

,

.

Среднему Т_М и всемирному Т_гр времени всегда приписывается дата, так как в основе календаря лежат средние солнечные сутки.

Часовые углы и звездное время даты не имеют.

Пример 3.1. Определить местное время в l = 37º52¢ W, если 31.Х Т_гр = 1^h23^m22^s

Решение.

l = 37º52¢ = 2^h31^m28^s

31.Х	Тгр	1^h23^m22^s
	l	–2^h31^m28^s
30.Х	ТМ	22^h52^m54^s

Пример 3.2. Определить время на меридиане Гринвича в, если 1.ХI Т_М = 21^h47^m36^s в l = 54º36¢ Е

Решение.

l = 54º36¢ = 3^h38^m24^s

1.ХI	ТМ	21^h47^m36^s
	l	–3^h38^m24^s
1.ХI	Тгр	18^h09^m12^s

§3.5. Поясное время

В повседневной жизни пользоваться местным средним солнечным временем неудобно, потому что местных систем счета времени в принципе столько же, сколько географических меридианов, т.е. бесчисленное множество. Поэтому для установления последовательности событий или явлений, отмеченных по местному времени, совершенно необходимо знать, кроме моментов, также и разности долгот тех меридианов, на которых эти события и явления имели место.

В 1884 году была предложена поясная система счета среднего времени, по которой весь земной шар делится на 24 часовые пояса, причем каждый пояс ограничен меридианами, расположенными друг от друга в 15º. Во всех точках земной поверхности, находящихся внутри каждого пояса, установлено пользование единым средним временем, соответствующим среднему местному времени на центральном меридиане данного пояса. Центральные меридианы каждого пояса располагаются в долготах, кратных 15º. Часовой пояс, в котором расположен Гринвич, считается нулевым, причем центральным меридианом этого пояса принят гринвичский меридиан. Меридианы в долготах 15, 30, 45º и т.д. к востоку от Гринвича являются центральными меридианами соответственно 1, 2, 3 и т.д. часовых поясов, расположенных к востоку от Гринвича; меридианы же в долготах 15, 30, 45º и т.д. к западу от Гринвича являются центральными меридианами 1, 2, 3 и т.д. часовых поясов, расположенных западнее Гринвича.

Границы каждого часового пояса расположены в 7º30¢ по долготе от центрального меридиана данного пояса к востоку и к западу. При такой системе расположения поясов времени разница между средними местным временем на меридиане, являющемся границей данного часового пояса, и средним местным временем на центральном меридиане пояса не превышает 30 ^m.

Таким образом, поясным временем называется среднее местное время на центральном меридиане часового пояса распространенное на всем протяжении данного пояса.

Поясное время нулевого часового пояса, т.е. среднее гринвичское время, называется всемирным временем Т_гр.

В один и тот же момент показания часов в разных часовых поясах отличаются друг от друга на целое число часов. Следовательно, в один и тот же момент разность между поясным временем и всемирным равна номеру часового пояса N

.

В тех случаях, когда меридианы, обозначающие границы часовых поясов, пересекают населенные пункты или административные районы, для устранения неудобств в пользовании поясным временем границу часовых поясов отодвигают и располагают вдоль условной линии.

Для определения номера часового пояса N следует заданную долготу разделить на 15º: если остаток меньше 7º30¢, та частное равно номеру часового пояса N; если остаток больше 7º30¢, то к частному прибавляется единица.

Пример 3.3. Определить номер часового пояса в долготе l = 137º52¢ W.

Решение.

и в остатке 2º52¢. Остаток меньше 7º30¢, поэтому частное 9 будет номером часового пояса, т.е. N = 9 W

Пример 3.4. Определить номер часового пояса в долготе l = 118º15¢ Е.

Решение.

и в остатке 13º15¢. Остаток больше 7º30¢, поэтому к частному 7 прибавляется единица и номер часового пояса будет 7 + 1 = 8, т.е. N = 8 E.

§3.6. Перевод поясного времени в среднее местное время
и наоборот. Судовое время

Перевод поясного времени в среднее местное время выполняется по формулам

, .

Для перехода от поясного времени к среднему местному времени рекомендуется всегда сначала получить всемирное время, а затем соответственно находить среднее местное время или поясное время.

Пример 3.5. Определить местное время Т_М в 28.Х Т_п = 2^h06^m41^s

Решение.

Определяем номер часового пояса N = 4 E.

Переведем долготу из дуговой меры в часовую l = 53º17,0¢ = 3^h33^m08^s

28.Х	Тп	2^h06^m41^s
	N	– 4
27.Х	Тгр	22^h06^m41^s
	l	3^h33^m08^s
28.Х	ТМ	1^h39^m49^s

Пример 3.6. Определить поясное время Т_п в l = 27º48,5¢ W если 16.III Т_М = 23^h05^m39^s

Решение.

Определяем номер часового пояса N = 2 W.

Переведем долготу из дуговой меры в часовую l = 27º48,5¢ = 1^h51^m14^s

16.III	ТМ	23^h05^m39^s
	l	+1^h51^m14^s
17.III	Тгр	0^h56^m53^s
	N	– 2
16.III	Тп	22^h56^m53^s

Часы, находящиеся в помещениях судна, устанавливаются по поясному времени, того пояса, в котором в данный момент находится судно. Время, по этим часам определяют с точностью до одной минуты, и называется судовым временем Т_с.

Судовым временем называется поясное время, по которому поставлены судовые часы и определяемое с точностью до одной минуты.

§3.7. Демаркационная линия

В системе поясного счета времени меридиан 180º является центральным меридианом 12 часового пояса и имеет восточную и западную части. Поясное время в восточной и западной части этого пояса одинаковое, но даты разные. По 180º меридиану Земли проходит линия смены дат – демаркационная линия. Официальная линия смены дат в некоторых районах Земли отклоняется от меридиана 180º, чтобы изменение даты не вызвали неудобств у местных жителей.

При пересечении демаркационной линии дату следует изменять, придерживаясь следующих правил:

1. Смену даты на судах принято производить в полночь, следующую за переходом.

2. При следовании судна восточными курсами следующей за пересечением демаркационной линии, на судне повторяется та же дата, что и была (рис.3.4).

3. При следовании западными курсами с полуночи следующей за пересечением линии смены дат, дата на судне изменяется сразу на две единицы.

4. При применении этих правил с момента пересечения 180º меридиана и до следующей полуночи долготы в расчетах считаются сверх 180º в том же направлении.

§3.8. Служба времени на судне

Для обеспечения производства астрономических наблюдений и решения задач, связанных с определением географических координат места судна и поправок компаса, необходимо в любой физический момент знать время гринвичского меридиана с точностью ± 0,2^s. Судовые часы, расположенные в служебных и жилых помещениях, должны показывать время с точностью до ± 0,5^m.

Для поддержания выше указанной точности показаний хронометра и часов на каждом судне организуется «Служба времени», на которую возлагается две основные задачи: определение и хранение точного времени.

Если поправка хронометра u_хр относительно всемирного времени известна, то в любой момент времени можно рассчитать всемирное время

,

где Т_хр – показания хронометра.

Определение поправок хронометра составляет одну из основных функций службы времени. От точного определения и хранения поправки хронометра зависит точность решения задач мореходной астрономии.

Астрономические наблюдения на судне производятся по обычным часам или при помощи секундомера. Поэтому для определения всемирного времени наблюдения необходимо знать поправку часов u_ч, которая обычно определяется по сличению часов с хронометром.

Сличением называется разность одновременных показаний хронометра и часов

.

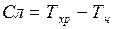Сличение может быть положительным и отрицательным и по абсолютной величине не превышает 6 часов.

Для повышения точности вычисления поправки часов по известной поправке хронометра и сличению рекомендуется делать 3-5 сличений и за окончательное принимать среднее значение. Сличение часов с хронометром производится в следующих трех случаях:

1) До и после завода хронометра;

2) каждый раз до и после определения поправки хронометра;

3) до и после астрономических наблюдений.

во всех перечисленных случаях сличение хронометра производится только с теми часами, которыми пользуются при астрономических наблюдениях.

Для организации повседневной жизни и вахтенной службы на судне предъявляются менее жесткие требования к точности времени. Для этой цели применяются судовые часы. Циферблат судовых часов разбит на 12 часов. Минутная шкала разбита на 60 делений. Пятые и десятые минуты оцифрованы. Штрихи и стрелки покрыты светящимся составом, позволяющим брать отсчеты по часам в темноте. Циферблат часов закрыт откидной крышкой, вставленной в металлический ободок. Судовые часы устанавливают в служебных и жилых помещениях.

Регулировка судовых часов производится при помощи индекса регулятора хода, расположенного в верхней части циферблата.

Завод судовых часов производится в каждый первый день недели в одно время с заводом хронометров.

В зависимости от системы счета времени судовые часы идут по поясному времени или по времени принятому в данном регионе (декретное время).

При переходе судна из одного часового пояса в другой судовые часы переводят на один час вперед (при движении судна на восток) или на один час назад (при движении судна на запад). Установка часов по новому поясу производится по приказу капитана судна в целый час по времени нового пояса после перехода судна в новою зону. Установку часов по новому поясу производят при помощи контрольных часов или секундомера.

§3.9. Календарь

Система счета длительных промежутков времени называется календарем. За многовековую историю человечества было разработано много различных систем календарей, которые можно разделить на три главных типа: солнечные, лунные и лунно - солнечные. В основе солнечных календарей лежит продолжительность тропического года, в основе лунных календарей – продолжительность синодического месяца [2]. Лунно-солнечные календари основаны на счете продолжительности, как тропического года, так и синодического месяца.

Современный календарь, принятый в большинстве стран, является солнечным календарем.

Основной единицей меры времени солнечных календарей является тропический год. Продолжительность тропического года составляет 365,2422 средних солнечных суток.

При составлении солнечного календаря необходимо выполнение двух условий:

1. Продолжительность календарного года, в среднем за несколько лет, должна быть как можно ближе к продолжительности тропического года.

2. Календарный год должен содержать целое число суток.

В юлианском календаре, разработанном александрийским астрономом Сизогеном и введенном Юлием Цезарем в 46 г. до н.э., эти условия выполняются соблюдением следующего правила: продолжительность календарного года считается равной 365 средним солнечным суткам три года подряд, каждый четвертый год содержит 366 средних солнечных суток.

Годы продолжительностью в 365 суток называются простыми, а в 366 суток – високосными. Високосными в юлианском календаре являются те годы, номера которых делятся на 4 без остатка. В високосном году в феврале 29 дней, а в простом – 28. Таким образом, продолжительность года в юлианском календаре в среднем за 4 года равна 365,25 средних солнечных суток, таким образом календарный год длиннее тропического всего на 0,0078 суток. Счет времени юлианскими годами за 128 лет дает расхождение со счетом тропическими годами приблизительно на 1 сутки, а за 400 лет – около 3 суток. Расхождение это практического значения не имеет, и юлианским календарем пользовались все европейские страны на протяжении 16 столетий.

Григорианский календарь возник в результате реформы юлианского календаря, произведенной в 1582 г. римским папой Григорием XIII из религиозных соображений.

Указанное расхождение юлианского календаря со счетом тропическими годами оказалось неудобным для церковного летоисчисления. По правилам христианский церкви праздник пасхи должен был наступать в первое воскресенье после полнолуния после дня весеннего равноденствия. В год, когда было установлено это правило на Никейском Соборе (325 г. н.э.), день весеннего равноденствия по юлианскому календарю припадал на 21 марта. В 1582 г., т.е. через 1257 лет день весеннего равноденствия приходиться уже на 11 марта. Этот переход дня весеннего равноденствия на более ранние даты вносил путаницу и неопределенность в определение дня пасхи и других христианских праздников. Реформа календаря, произведенная по проекту итальянского математика и врача Луиджи Лилио, предусматривала, во-первых, возвращение календарной даты 21 марта на день весеннего равноденствия и, во-вторых, изменение в правиле счета простых и високосных лет с целью уменьшения расхождения со счетом тропическими годами. Поэтому в булле папы Григория XIII имелось два принципиальных пункта:

1. После 4 октября 1582 г, считать не 5, а 15 октября.

2. Не считать в дальнейшем високосными те годы столетий, у которых число сотен не делиться без остатка на 4 (например, високосными не являются 1800, 1900, 2100).

Первым пунктом этого постановления устранялось расхождение в 10 суток юлианского календаря со счетом тропическими годами.

Вторым пунктом продолжительность календарного года в среднем за 400 лет устанавливалась равной 365,2425 средних солнечных суток. Таким образом, средний календарный год стал длиннее тропического всего на 0,0003 суток и счет времени по григорианскому календарю и тропическими годами даст расхождение в 1 сутки только через 3300 лет. Исходя из этого дальнейшее совершенствование григорианского календаря в этом направлении нецелесообразно.

Григорианский календарь был введен в большинстве западных стран в течении XVI-XVII вв. В России перешли на новый стиль только в 1918 г. В этом году, по декрету Советского правительства, вместо 1 февраля стали считать 14 февраля, так расхождение юлианского календаря со счетом тропическими годами к 1918 г. составляло уже 13 суток. С 28 февраля 2100 г. расхождение юлианского календаря со счетом тропическими годами составит 14 суток.

Начало календарного года понятие условное. Так в России до XV в. первым днем года считали 1 марта, а с XV в. до 1700г. – 1 сентября. С 1700 г. за начало года стали считать 1 января.

Начало счета календарных годов называется эрой. В древности и в средние века существовало множество эр: «от сотворения мира», от воцарения разных государей (например, эра Диоклетиана). Наша – новая эра имеет счет от «рождества Христова» введенная ученым монахом Дионисием в 525 г.н.э. (1278 г. от «основания Рима»). Не дав никаких объяснений, Дионисий объявил, что Христос родился в 753 г. от «основания Рима». В России новая эра введена с 1 января 1700 г. до этого счет велся от «сотворения мира» (шел 7208 г. от «сотворения мира»).

Установление двенадцати месяцев в году и семи дней в недели имеет астрономическое обоснование.

Так продолжительность месяца приблизительно равна продолжительности времени возвращения Луны в одноименную фазу. Время между фазами равна одной четвертой части месяца, т.е. приблизительно 7 дней – неделя. Названия дни недели получили по названиям тогда известных небесных светил: Солнце, Луна, Меркурий, Венера, Марс, Юпитер, Сатурн.

Глава IV
Морской астрономический ежегодник

§4.1. Назначение и устройство
Морского астрономического ежегодника

Астрономическим ежегодником называется собрание астрономических таблиц, содержащих главным образом видимые координаты светил на период определенного календарного года и другие астрономические величины.

Морской астрономический ежегодник предназначен для получения гринвичских часовых углов и склонений светил на любой момент времени, а также некоторых других величин, используемых при решении ряда задач морской астронавигации.

Первый астрономический ежегодник был издан в 1679 г. Парижской обсерваторией.

с 1767 г. начал издаваться английский астрономический ежегодник под названием „Морской альманах и астрономические эфемериды[3]”. С 1815 г. по инициативе академика Ф.И.Шуберта начал издаваться русский „Морской месяцеслов”, по структуре подобный английскому ежегоднику. Издание „Морского месяцеслова” было прекращено в 1856 г., и с этого времени в России перешли на пользование иностранными ежегодниками вплоть до 1922 г., когда Институт теоретической астрономии Академии наук СССР начал издавать „Астрономический ежегодник СССР”. Американский ежегодник издается с 1855 г. В названиях всех этих ежегодников отражалась морская направленность, однако никаких других ежегодников в те времена не издавалось, и они были общими для целей астрономии, геодезии и судовождения. Ежегодники, изначально издаваемые для потребностей мореплавания, постепенно эволюционировали в сторону обеспечения задач геодезии и общей астрономии. Они расширились настолько, что стало необходимым издавать раздельно специализированные астрономические ежегодники: основные, морские, а позднее авиационные.

С 1851 г. Германия и с 1889 г. во Франции издается „Морской астрономический ежегодник”, в Англии „Морской альманах сокращенного содержания для пользования мореплавателями” начал издаваться с 1914 г.

Первый „Морской астрономический ежегодник” в СССР вышел в1930 г.

Российский „Морской астрономический ежегодник”

Современный вид Российский „Морской астрономический ежегодник” (МАЕ) получил с 2001 года, и содержит координаты Солнца, Луны, планет и наиболее ярких звезд; сведенья относительно восхода и захода Солнца и Луны и продолжительности сумерек под различными широтами и другие сведенья.

В начале МАЕ приводится содержание.

Затем следует пояснение к пользованию Морским астрономическим ежегодником, в котором изложены основные положения о времени и счете времени. Описываются основные таблицы и приложения. Приведены принятые в МАЕ обозначения и формулы. Даны примеры решения ряда различных задач, которые могут встретиться при использовании МАЕ.

Далее приведены «Некоторые явления в Солнечной системе», т.е. приводятся сведенья о моментах равноденствий и солнцестояний, элонгаций, соединений и противостояний планет, а также приводятся сведенья о солнечных и лунных затмениях; указываются возраст и фазы Луны на 0 часов всемирного времени каждого дня.

В разделе „Видимость планет” на каждый месяц приводятся условия видимости четырех навигационных планет: Венеры, Марса, Юпитера и Сатурна.

Далее следуют таблицы, занимающие основную часть Морского астрономического ежегодника – „Ежедневные таблицы”, в которых для трех последовательных суток приводятся следующие величины:

1. Вверху в каждой странице даны: год, название месяца, даты и порядковые номера соответствующих трех дней года. С левой стороны страницы указаны даты, названия дней недели и всемирное время Т_гр от 0 до 23 часов для каждых суток.

2. Для каждого часа всемирного времени Т_гр приводятся:

а) гринвичские часовые углы t_гр для точки Овна, Солнца,

Венеры, Марса, Юпитера, Сатурна и луны;

б) склонения d для Солнца, Венеры, Марса, Юпитера, Сатурна и луны.

3. Между последовательными табличными значениями гринвичских часовых углов Солнца, планет и Луны даны квазиразности . Квазиразность – это разность между действительным изменением часового угла светила за один час среднего времени и наименьшим возможным изменением часового угла за тот же промежуток времени.

Для Солнца и планет ; для Луны , где D – обычная разность двух последовательных величин ( и – это наименьшие возможные изменения часовых углов за один час всемирного времени). Для Луны квазиразности меняются быстро, и поэтому они даны на каждый час справа от столбца значений гринвичских часовых углов Луны. Для Солнца и планет квазиразности меняются медленно, и в таблицах указаны их средние значения за данные трое суток внизу столбца соответствующих часовых углов. Квазиразности всегда положительны.

4. Между последовательными табличными значениями склонений Солнца, планет и Луны даны разности D. Для Луны разности D быстро меняются, и поэтому они даны на каждый час справа от столбца значений склонений Луны. Для Солнца и планет эти разности меняются медленно, и в таблицах их средние значения за данные трое суток внизу столбца соответствующих склонений. Разности могут быть как положительными, так и отрицательными.

5. Звездные величины планет приведены справа от названия планет.

6. На среднюю дату соответствующего трехсуточного интервала на левой странице в нижней строке для планет даны:

а) момент всемирного времени верхней кульминации на меридиане Гринвича Т_к;

б) прямое восхождение a;

в) горизонтальный экваториальный параллакс р ₀.

7. На каждый день года на правой странице разворота внизу даны: величина h – уравнение времени[4], моменты среднего времени верхней кульминации Солнца, а также верхней и нижней кульминации Луны на меридиане Гринвича. На 0^h всемирного времени каждого дня приведены значения: полудиаметра R Солнца и Луны, горизонтального экваториального параллакса Луны р ₀, возраст Луны. Фаза Луны для трехсуточного интервала изображена одним из восьми различных значков, показывающих величину освещенной части лунного диска для северной широты.

8. На среднюю дату трехсуточного интервала даны моменты среднего времени на меридиане Гринвича видимых восхода и захода верхнего края Солнца для наблюдателя, находящегося на уровне моря при температуре воздуха + 10°С и атмосферном давлении 760 мм.рт.ст. для 30 значений широт от 60° S до 74° N.

9. На среднюю дату трехсуточного интервала даны моменты всемирного времени начала и конца утренних и вечерних навигационных и гражданских сумерек. Указанные в таблицах моменты начала и конца сумерек можно использовать для любой даты данного трехсуточного интервала. Когда гражданские или навигационные сумерки на какой-либо широте продолжаются всю ночь, то в данном месте ставится символ ///. В высоких широтах Солнце и Луна могут в течение суток находиться над горизонтом или под горизонтом. Эти явления обозначаются символами ¢ и £ соответственно. Иногда в высоких широтах Луна восходит или заходит дважды в течение суток. В таких случаях в соответствующей строке даны два момента восхода или захода Луны.

10. На каждый день года даны момента среднего времени видимых восхода и захода верхнего края Луны для наблюдателя, находящегося на меридиане Гринвича на уровне моря, для 30 различных широт от 60° S до 74° N. Если для какой-либо широты для момента восхода или захода Луны стоит прочерк, то это показывает, что в данные сутки соответствующее явление в указанной широте не происходит.

11. На правом развороте ежедневных таблиц приведены видимые места 67 наиболее ярких звезд, включая Полярную. Для каждой звезды дано ее звездное дополнение и склонение.

12. На каждый день года даны значения азимутов (в круговом счете) верхнего края диска Солнца в моменты его восходов или заходов, используемые для определения поправки компаса.

Кроме ежедневных таблиц в ежегоднике приводятся и другие таблицы.

Таблица «Звезды. Видимые места» содержит видимые места 160 звезд (включая полярную). Координаты светил (звездное дополнение и склонение) приводятся на первое число каждого месяца. Для каждой звезды приводится ее величина и среднее для данного года значение прямого восхождения.

Таблица «Азимут Полярной» позволяет получить азимут Полярной звезды по звездному времени и широте.

Таблица «Широта по высоте Полярной» содержит первую, вторую и третью поправки, позволяющие рассчитать широту места по наблюденной высоте Полярной.

«Основные интерполяционные таблицы» (приложение 4) служат для расчета часовых углов и склонений на промежуточные моменты между целыми значениями часов всемирного времени. Они содержат 60 таблиц, озаглавленных минутами 0^m, 1^m, …, 59^m. В каждой таблице имеется пять колонок. В трех колонках, расположенных слева, для данной минуты, указанной в заголовке таблицы, и данной секунды, указанной в вертикальном столбце слева от таблицы, приведены величины изменения часового угла точки Овна, Луны, Солнца и планет. В двух колонках, расположенных справа, по аргументу квазиразности даются всегда положительные поправки к табличному изменению, учитывающие отклонение фактического изменения часового угла от указанных значений. Для точки Овна эта дополнительная поправка всегда равна нулю. Данными этих же двух колонок следует пользоваться и при интерполировании склонений светил на промежуточные моменты наблюдения. В них даются соответствующие пропорциональные части по аргументу разности D. Эти пропорциональные части имеют знак, соответствующий знаку разности D.

Модифицированные «Таблицы для вычисления высоты и азимута ТВА-52» (приложение 5) предназначены для вычисления высоты и азимута при определении места судна в море по наблюдениям светил.

Дата добавления: 2015-10-29