Эффект Ганна.

В 1963 г. Джон Ганн, изучая поведение арсенида галлия в области сильных полей, обнаружил новое явление, заключающееся в возникновении колебаний тока с частотой 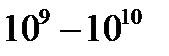Гц при приложении к кристаллу постоянного электрического поля. Этот эффект Ганна наблюдали позднее в фосфиде галлия.

В основе эффекта Ганна лежит междолинное рассеяние носителей заряда. Что такое междолинное рассеяние? Это рассеяние (т.е. изменение состояния электрона) сопровождающееся перебросом электронов из одного минимума в другой. Необходимым условием этого является наличие нескольких минимумов зоны проводимости.

Рассмотрим схематично зонную структуру арсенида галлия, зависимость энергии электрона в зоне проводимости от волнового вектора κ имеет вид:

Существенным здесь является наличие двух минимумов А и Б, разделённых энергетическим зазором DE=0.36эВ. Поскольку кривизна зависимости E(k) в области этих двух экстремумов различно, то различаются и эффективные массы электронов, находящиеся в этих минимумах. В области минимума А 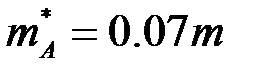(т.е. электроны лёгкие). В области минимума Б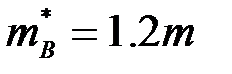 (т.е. электроны тяжёлые). Подвижность электронов связана с их эффективной массой соотношением 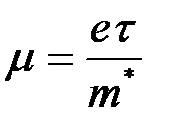. Следовательно, подвижность лёгких электронов должна быть выше, чем тяжёлых. Для GaAsm лёгких составляет (4000- 8000см*см/Всек),m тяжёлых составляет ~(100-200 см*см/Всек).

Т.о., при переходе электронов из минимума А в Б подвижность их изменяется.

Теперь рассмотрим действие электрического поля на носители заряда. При малых внешних электрических полях электроны будут находиться в термодинамическом равновесии с решёткой, имеющей температуру . Поскольку , то электроны будут занимать энергетические уровни минимума А. Плотность тока будет определяться концентрацией и подвижностью лёгких электронов

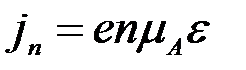
По мере возрастания напряжённости электрического средняя энергия электронов повышается и становится возможным переход электронов во второй минимум Б, где они будут обладать малой подвижностью. Следовательно, с ростом напряжённости поля имеет место изменения скорости элетронов. Это скажется на величине плотности тока. Скорость движения электрона, а значит, и плотность тока будут линейно возрастать с ростом напряжённости поля до некоторого критического значения.

При электроны, рассеиваясь, переходят в более высокий минимум, где они будут обладать большей массой. Подвижность электронов, а, следовательно, скорость движения электронов резко падают и плотность тока резко понижается до значений 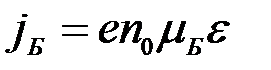. На ВАХ появится падающий участок.падающий участок будет иметь место и на графике зависимости скорости движения электронов от напряжённости поля, который имеет вид:

Рассмотрим более подробно механизм электронной неустойчивости, приводящей к высокочастотным осцилляциям тока. Пусть к образцу длинной L приложено внешнее электрическое поле.

В однородном п/п-ке электрическое поле примерно одинаково по всей длине. Но если в образце имеется некоторая неоднородность с повышенным сопротивлением (заштрихованная область), то напряжённость этого поля в этом месте образца будет несколько выше. Следовательно при повышении напряжённости поля возникнет в первую очередь в этом сечении образца. Как только напряжённость поля достигнет 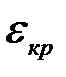,имеет место переход электронов в высокий минимум в область образца с повышенной напряжённостью поля.

Здесь концентрация тяжёлых электронов возрастает. Т.к.

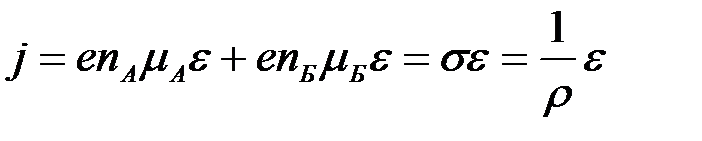
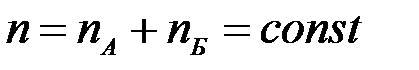
т.е. общая концентрация неизменна, то r, т.е. сопротивление, возрастает. Это приводит к возрастанию напряжённости поля в этом месте образца, что в свою очередь вызывает более интенсивный переход электронов в верхние минимумы. Справа и слева от этой области напряжённость поля будет падать и распределение поля становится резко неоднородным. Такая зона с сильным элктрическим полем получило название электрического домена.

Домен, содержащий тяжёлые электроны, под действием поля перемещается вдоль образца с относительно низкой скоростью, т.к. подвижность тяжёлых электронов мала. Лёгкие электроны также перемещаются в поле, причём с большей скоростью. Те электроны, которые движутся сзади домена, догоняют его и образуют область отрицательного объёмного заряда, а те, которые движутся впереди, уходят от домена, и таким образом формируется область, обеднённая электронами т.е. область положительного объёмного заряда.

Через некоторое время устанавливается стационарное состояние, при котором скорость движения домена равна скорости перемещения электронов вне домена. Это происходит потому, что поле внутри домена сильно возросло Þ возрастает скорость движения электронов в нём. Поле вне домена, наоборот, резко снижается. Поэтому дрейфовая скорость электронов за пределами домена. Когда домен достигнет границы образца, он разрушается.

Пусть внешнее напряжение прикладывается к образцу в момент времени 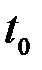. Сразу же на одной из неоднородностей начинается образование домена. Этот процесс протекает очень быстро, т.к. постоянная времени, связанная с переходом электронов из минимума А в Б составляет примерно 10 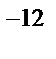сек. Сила тока резко понижается до значения Imin, определённого скоростью движения домена:

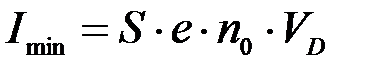
S- площадь сечения образца.

Это значение тока сохраняется до тех пор, пока домен не разрушится на границе образца. Очевидно, что время движения домена:

По достижении конца образца домен начинает разрушаться и ток возрастает до Imax. Снова образуется домен и ток уменьшается. Так возникает колебания тока. Частота колебаний определяется длиной образца. Например, при L=50мкм она составляет 2ГГц

Скорость движения домена не зависит от внешнего поля и составляет 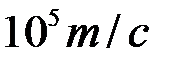. Поле изменяет лишь толщину домена.

Несмотря на то, что в кристалле может быть несколько неоднородностей, на которых могут формироваться домены, однако в кристалле существует только один домен. Другими словами возникновение домена происходит только на одной из неоднородностей. Разное расположение неоднородностей в кристалле определяет разные пролётные времена доменов, т.е. разный период колебаний. поэтому для наблюдения эф. Ганна необходимы чистые и очень однородные образцы.

Дата добавления: 2015-10-31