Короткі теоретичні відомості. Цифрові системи керування, так само які безперервні системи

Цифрові системи керування, так само які безперервні системи, повинні мати певні якісні показники (запас стійкості, точність, швидкодія). Способом забезпечення необхідних динамічних властивостей таких систем є використання дискретної корекції, реалізованої шляхом вибору алгоритму роботи цифрової обчислювальної машини (ЦОМ). Застосування дискретної корекції порівняно з безперервними коригувальними ланцюгами дозволяє більш точно реалізувати бажаний закон управління, спростити перебудову параметрів або навіть структури коригувального пристрою при зміні умов роботи системи.

Одна з можливих структурних схем системи управління з ЦОМ при введенні дискретної корекції зображена на рис. 6.1. Для цієї структурної схеми дискретна передавальна функція розімкнутого контуру системи має вигляд

де – дискретна передатна функція наведеної безперервної частини системи з урахуванням екстраполятора нульового порядку; – коефіцієнти передачі лінеаризованих АЦП і ЦАП.

Якщо відома бажана дискретна передавальна функція розімкнутого контуру системи , то з умови можна визначити дискретну передавальну функцію ЦВМ:

. (6.1)

Рисунок 6.1 – Структурна схема одноконтурної замкнутої цифрової системи

У даній лабораторній роботі об’єктом регулювання є двигун постійного струму незалежного збудження. За вихідну координату об'єкта регулювання взято переміщення і не враховується електромагнітна стала часу. В цьому випадку передавальна функція двигуна описується інтегруючою ланкою другого порядку

, (6.2)

де – коефіцієнт передачі, виражений в мм/В. Перейдемо від безперервної передавальної функції об’єкта регулювання до z-передавальної функції. Задамося інтервалом дискретності, введемо запам’ятовуючий елемент нульового порядку. При взятих положеннях вираз (6.2) набуде вигляду:

, (6.3)

де K – – загальний коефіцієнт розімкнутого контуру управління.

Визначимо частотні характеристики наведеної безперервної частини. Для цього за допомогою перетворення

(6.4)

перейдемо на w площину, а потім в отриманому виразі здійснимо підстановку

, (6.5)

де – абсолютна псевдочастота.

У результаті виконаних перетворень отримаємо частотну характеристику наведеної безперервної частини у функції абсолютної псевдочастоти

. (6.6)

Відомо, що псевдочастота пов’язана з круговою частотою співвідношенням .

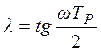При 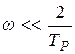частотні характеристики безперервної системи у функції колової частоти і наведеної системи у функції абсолютної псевдочастоти практично збігаються. На рис. 6.2 в пакеті Control System Toolbox наведені логарифмічні частотні характеристики безперервної частини розміщеної системи у функції колової частоти, побудовані за виразом (6.2), і частотні характеристики дискретної системи у функції абсолютної псевдочастоти , побудовані
за виразом (6.4). Як видно з цього рисунка, в області середніх частот логарифмічні амплітудно-частотні характеристики збігаються, що свідчить про правильний вибір параметра .

% Визначення параметрів безперервних і дискретних

% коригувальних пристроїв.

h1=tf(5,[1,0,0]) % Передавальна функція об'єкта.

T=0.1 % Інтервал дискретності.

hh=c2d(h1,T) % Визначення Z-передавальної функції

% дискретної розташованої системи.

h=tf(5*[-0.05,1],[1,0,0]) % Частотні характеристики дискретної

figure(1) % розташованої системи у функції псевдочастоти

bode(h,h1) % Частотні характеристики розташованої системи

% у функції колової частоти і псевдочастоти

w1=tf([1,1],[1,10]) % Параметри безперервного коригувального

% пристрою.

k=1 % Коригувальний множник, що враховує

% вплив коригувальних пристроїв

% на коефіцієнт підсилення

g=k*h1*w1 % Частотні характеристики безперервної

% скоригованої системи в

% функції колової частоти.

w1d=tf([1,1],[1,10]) % Частотні характеристики дискретної

gd=k*h*w1d % системи у функції псевдочастоти.

figure(2) % ЛАЧХ систем:

% h1-безперервної нескоригованої;

bode(g,gd,h1) % g-безперервної з безперервним

% коригувальним пристроєм у функції частоти;

% gd-дискретної з дискретним коригувальним пристроєм.

На рис. 6.2, а показано, що частотні характеристики скоригованої і не скоригованої безперервної і дискретної системи в області низьких і середніх частот збігаються. Відмінність у характеристиках спостерігається в області високих частот (при частоті, яка в 10 разів перевищує частоту зрізу системи), що практично не позначається на якості перехідних процесів. Такий вид частотних характеристик свідчить про те, що інтервал дискретності узятий правильно. Якщо збільшити, то діапазон частот, у якому характеристики збігаються, збільшиться.

Відмінність у фазових характеристиках істотна. Але вона пов’язана не з відмінністю фізичних процесів, що протікають у безперервних і дискретних системах регулювання, а з відмінністю від рахунків фазових зсувів. При використанні псевдочастоти математично визначається фазовий зсув для гострого кута, а фактично фазовий зсув більше 180°. Тому до кута, визначеного програмою MatLab, слід додати постійне запізнювання -180°. З урахуванням цього запізнювання відмінності між фазовими характеристиками, побудованими у функції колової частоти і псевдочастоти, буде незначним.

а)

б)

Рисунок 6.2 – ЛАФХ безперервної і дискретної систем регулювання:

а) ЛАФХ вихідних (не скоригованих) систем регулювання:1 (h1) –частотні характеристики безперервної системи регулювання у функції колової частоти, 2 (g1) –дискретної системи у функції абсолютної псевдочастоти;

б) ЛАФХ вихідної і скоригованої систем регулювання:1 (h1) – безперервна нескорегована система, 2, 3 (g, gd) – безперервна з аналоговим коригувальним пристроєм і дискретна з дискретним коригувальним пристроєм.

Частотні характеристики розташованої (нескорегованої) системи 2 (g) і
1h (1) перетинають лінію 0 дБ з нахилом -40 дБ/дек (рис.6.2, а). Це вказує на незадовільну якість перехідного процесу. Про це свідчать і фазові характеристики (фазовий зсув на частоті зрізу більше -180°).

Для задовільної якості перехідного процесу необхідно, щоб логарифмічна характеристика скоригованої системи перетинала лінію 0 дБ з нахилом
-20 дБ/дек. Причому протяжність ділянки з нахилом -20 дБ/дек повинна складати (2¸4) октави: (1¸2) октави ліворуч від частоти зрізу і (1¸2) октави праворуч від частоти зрізу. Чим більше довжина ділянки середніх частот з нахилом -20дБ/дек, тим більший запас по фазі і тим менше перерегулювання.

Для покращення якості перехідного процесу слід ввести пропорційно-диференційну ланку, яка на ділянці середніх частот змінить нахил логарифмічної нескоригованої системи з -40 дБ/дек на -20 дБ/дек. Параметри коригувального пристрою визначаються видом ЛАЧХ розташованої системи 2g(1). З рис.2.а випливає, що частота зрізу розташованої системи дорівнює 2,4 рад/сек. Виходячи з вимог до протяжності ділянки з нахилом -20дБ/дек слід ввести безперервно коригувальний пристрій, диференціювальна частина якого включається при
w = 1 рад/сек, а вимикається при w = 10рад/сек.

. (6.7)

Так як на ділянці середніх частот характеристики безперервної системи у функції w і цифрової системи у функції l збігаються, то характеристика цифрового коригувального пристрою у функції l визначається виразом, що збігається з виразом (6.5)

. (6.8)

На рис. 6.2,б представлені ЛАЧХ скоректованої аналогової 2 (g) і цифрової
3 (gd) систем після введення коригувальних ланок. Як видно з графіків, введення коригувальної ланки зміни в амплітудно-частотні характеристики в необхідний бік: скориговані системи (аналогова і дискретна) перетинають лінію 0 дБ з необхідним нахилом -20 дБ/дек, але зменшується коефіцієнт підсилення. В області низьких частот характеристики скоригованих систем (аналогової і дискретної) збігаються; в області високих частот збігаються характеристики аналогових систем: вихідної та скоректованої. Відмінність характеристик дискретної скоригованої системи від аналогової скоригованої виявляється тільки на високих частотах.

Введення коригувального пристрою (6.5) зменшує коефіцієнт підсилення розімкнутої системи в 10 разів: частотні характеристики скоригованих систем (аналогової і дискретної) в області низьких частот розташовані нижче частотних характеристик вихідної системи. Зменшення коефіцієнта підсилення розімкнутої системи за рахунок введення коригувальних пристроїв повинно бути скомпенсовано відповідним збільшенням коефіцієнта підсилення будь-якої ланки, наприклад, безперервної частини системи.

Для реалізації цифрового регулятора необхідно мати дискретну передавальну функцію, яку отримаємо з (1-6) шляхом підстановки

. (6.9)

Щоб спростити вираз (6.7), беремо, що коефіцієнт підсилення регулятора дорівнює одиниці. Коефіцієнт 0,7, отриманий у виразі (6.7), і коефіцієнт 10, отриманий при введенні коригувального пристрою, буде компенсований відповідною зміною коефіцієнта підсилення безперервної частини системи.

З урахуванням цих зауважень передавальній функції (6.7) буде відповідати різницеве рівняння

, (6.10)

реалізація якого вимагає чотирьох осередків стекової пам’яті, двох блоків множення і суматора. У двох осередках стекової пам’яті повинні зберігатися коди помилок на даному інтервалі дискретності і на попередньому. Причому, сигнал на попередньому інтервалі повинен бути взятий з вагою 0,9. У наступних двох осередках стекової пам’яті повинні зберігатися коди керуючого сигналу (виходи регулятора). Причому, сигнал на попередньому інтервалі дискретності повинен бути взятий з вагою 0,33. Поточне значення виходу цифрового регулятора визначається виразом (6.8). Структурні схеми безперервної та цифрової систем регулювання, зібрані в пакеті Simulink, представлені на рис. 6.3.

Рисунок 6.3 – Структурні схеми безперервної та цифрової систем регулювання

Для безперервної системи корекція виконана безперервним коригувальним пристроєм з передавальної функції, яка визначається виразом (6.5). Коефіцієнт підсилення безперервної частини збільшено в 10 разів. Для дискретної системи корекція виконана цифровим регулятором, параметри якого визначені виразом (6.7). Безперервна частина системи з дискретною частиною з членована запам’ятовуючими елементами нульового порядку. Інтервал дискретності цифрового регулятора та запам’ятовуючих елементів нульового порядку однаковий і дорівнює . Коефіцієнт підсилення безперервної частини збільшено в 7 разів.

На рис. 6.4 представлена ще одна модель цифрової системи, безперервна частина якої визначається виразом (2), а коригувальний пристрій має вигляд:

. (6.11)

Коригувальний пристрій (6.9) порівняно з коригувальним пристроєм (6.5), збільшує протяжність ділянки з нахилом -20 дБ/дек і значно (в 100 разів) зменшує коефіцієнт підсилення розімкнутої системи.

Рисунок 6.4 – Налаштування блоку Discrete Transfer Fcn

Розрахунок дискретної корекції виконаний за наведеною вище методикою:

(6.12)

Коефіцієнт підсилення розімкнутої системи відновимо, збільшивши коефіцієнт підсилення безперервної частини. Які слід було очікувати, збільшення протяжності ділянки з нахилом -20дБ/дек покращує якість перехідного процесу. Про це свідчать порівняльні характеристики перехідних процесів трьох систем.

Дата добавления: 2015-10-24