Порядок виконання роботи. 1. Дослідженню підлягає система другого порядку, лінійна частина якої має

1. Дослідженню підлягає система другого порядку, лінійна частина якої має передавальну функцію:

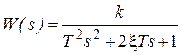. (2.4)

Значення коефіцієнта підсилення k, сталої часу Т і коефіцієнта демпфірування наведено в таблиці 2.1.

2. Відповідно до свого варіанта виконати моделювання лінійної розімкнутої системи (на вхід подати одиничний ступеневий сигнал 1(t)).

Для кожного із чотирьох заданих значень коефіцієнта побудувати фазовий портрет системи (використовуючи XYGraph) і відповідну перехідну характеристику (рис. 2.2). Зробити висновки.

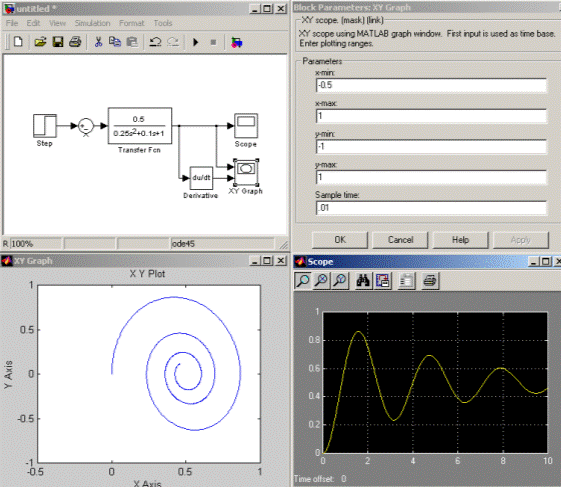
Рисунок 2.2 – Приклад схеми моделі лінійної системи другого порядку

(з блоком параметрів XYGraph) для побудови фазового портрета й перехідної характеристики

Блок XYGraph здійснює вивід двохкоординатного графіка. У блоці параметрів можна задавати:

- х min, xmax, у min, у max – мінімальні й максимальні значення за координатами х і у;

- Sample Time – період дискретизації (для отримання гладких кривих необхідно ввести значення 0,1 або 0,01).

Слід пам’ятати, що координата у є похідною від координати х. Тому на вхід Y подається вихідний сигнал системи через блок диференціювання du/dt.

3. Замкнути систему. До зворотного зв’язку ввести нелінійний елемент (рис. 2.2, в) з параметрами статичної характеристики, що задані в таблиці 2.1 (відповідно до свого варіанта). Побудувати фазовий портрет нелінійної системи і відповідну перехідну характеристику. Зробити висновки.

4. Повторити пункт 3 для нелінійних елементів (рис. 2.2, г, е).

Таблица 2.1 – Варіанти завдань

Параметр	Варіант
k
Т	0,5			0,8	1,5
x1
x2	0,1	0,3	0,5	0,2	0,6
x3	-0,5	-0,3	-0,4	-0,6	-0,4
x4	1,5		2,5

Зміст звіту

1. Схема моделі.

2. Фазовий портрет і перехідна характеристика для кожного досліджуваного випадку.

3. Висновки.

Контрольні питання

1. У чому полягає сутність дослідження нелінійних систем методом фазової площини?

2. Що таке фазова траєкторія? Фазовий портрет?

3. Назвіть основні особливості фазового портрета.

4. Що таке особлива точка?

5. Який вигляд має фазовий портрет системи з незатухаючими коливаннями із затухаючими коливаннями, із коливаннями, що розходяться?

6. Чим вирізняються фазові портрети лінійних і релейних систем?

7. Чим обмежується застосування методу фазової площини?

Література: [2, с. 372–386].

Лабораторна робота № 3

Тема. Дослідження режиму автоколивань

Мета: Набуття навичок дослідження режиму автоколивань нелінійних систем графоаналітичними методами та засобами пакета "Matlab".

Дата добавления: 2015-10-24