Короткі теоретичні відомості. 1 Перелік лабораторних робіт

ЗМІСТ

Вступ.................................................................................................................... 4

1 Перелік лабораторних робіт........................................................................... 5

Лабораторна робота № 1 Моделювання типових нелінійностей............ 5

Лабораторна робота № 2 Вивчення фазових портретів систем............ 12

Лабораторна робота № 3 Дослідження режиму автоколивань............. 18

Лабораторна робота № 4 Перетворення форм представлення безперервних і дискретних операторів. Побудова частотних характеристик розімкнутої імпульсної САК.................................................................................................................... 28

Лабораторна робота № 5 Синтез регуляторів...........................................

Лабораторна робота № 6 Дослідження цифрових систем регулювання..

2 Критерії оцінювання знань студентів................................................................

Список літератури............................................................................................. 57

ВСТУП

Дисципліна «Теорія автоматичного керування» лежить в основі всіх дисциплін, які вивчають прикладні питання автоматизації.

Метою її вивчення є:

– освоєння принципів побудови різних типів систем автоматичного керування (САК);

– вивчення властивостей і особливостей лінійних, нелінійних і дискретних САК;

– освоєння методів аналізу стійкості та якості перехідних процесів різних САК;

– освоєння методів синтезу коректувальних пристроїв з метою отримання необхідних властивостей САК.

Методичні вказівки щодо виконання лабораторних робіт присвячені вивченню і дослідження дискретних систем.

У результаті вивчення дисципліни і виконання другої частини лабораторних робіт студент повинен:

Знати:

- загальні методи теорії керування;

- питання імпульсних і цифрових систем керування;

- методи оцінки стійкості, якості, способи корекції імпульсних систем;

- питання синтезу цифрових систем

Уміти:

- застосувати методи модального керування для синтезу дискретних (імпульсних і цифрових), оптимальних, адаптивних систем автоматичного керування;

- застосовувати методи оцінювання стійкості, якості, а також способи корекції імпульсних САК;

- виконувати синтез цифрових систем.

ПЕРЕЛІК ЛАБОРАТОРНИХ РОБІТ

Лабораторна робота № 1

Тема. Моделювання типових нелінійностей

Мета: Набуття навичок моделювання типових нелінійностей за допомогою пакета програм "Matlab".

Короткі теоретичні відомості

Лінійні системи автоматичного керування (САК) описують лінійними диференціальними рівняннями. У цих рівняннях змінні та їх похідні зустрічаються лише у першому степені й відсутні взаємні добутки змінних та їх добутки з похідними.

На практиці лінійних САК не існує, бо характеристики більшості елементів, що утворюють системи, нелінійні, й точні диференціальні рівняння систем є нелінійними. У них, крім першого, зустрічаються й інші степені змінних та їх похідних. До нелінійних САК належать усі системи, до яких входить один або декілька нелінійних елементів. Таким чином, нелінійність систем зумовлена нелінійністю статичної характеристики одного з її елементів.

Найпростішими нелінійними елементами є статичні нелінійності. У них вихідна величина y залежить тільки від вхідної величини x, причому ця залежність є однозначною (рис. 1.1, а, в; рис. 1.2, а, б, г).

У динамічних нелінійностей вихідна величина y залежить як від вхідної величини x, так і від її похідної x ¢. Характеристика динамічної нелінійності завжди неоднозначна. Це петльові характеристики (рис. 1.1, б; рис. 1.2, д, е). Більш складною динамічною нелінійністю є елемент із сухим тертям або ідеальне реле, що часто зустрічається в технічних пристроях (рис. 1.2, в).

а) елемент з насиченням; б) гістерезис; в) випрямляч

Рисунок 1.1 – Типові нелінійні характеристики

Досить часто зустрічаються елементи, характеристики яких є частково-

лінійними або апроксимуються частково-лінійними графіками (рис. 1.2).

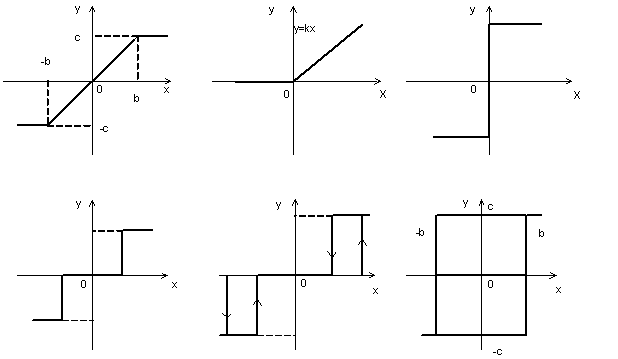
а) – характеристика з насиченням; б) – ідеальний випрямляч;
в) – ідеальне реле; г) – трипозиційне реле із зоною нечутливості;
д) – трипозиційне реле із зоною нечутливості та гістерезисом;
е) – двопозиційне реле з гістерезисом

Рисунок 1.2 – Типові частково-лінійні характеристики

Якщо до системи входить декілька нелінійних елементів, з’єднаних послідовно, паралельно або зустрічно-паралельно, то сумарну характеристику можна побудувати за певними правилами.

Паралельне з’єднання нелінійних елементів. При паралельному з’єднанні НЕ сумарну характеристику будують як геометричну суму нелінійних характеристик окремих елементів (рис. 1.3).

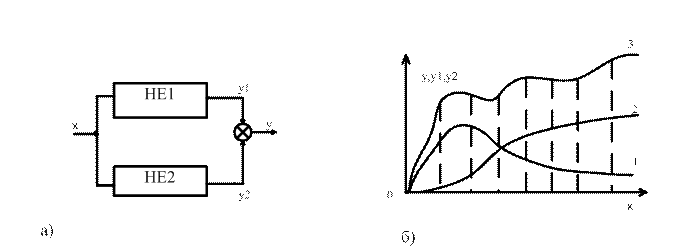
а) – структурна схема паралельного з’єднання нелінійних елементів;
б) нелінійні характеристики елементів (1 і 2) і сумарна характеристика (3)

Рисунок 1.3 – Паралельне з’єднання нелінійних елементів

Послідовне з’єднання двох нелінійних елементів. При послідовному з’єднанні нелінійних елементів вихідна величина одного НЕ є вхідною для подальшого НЕ (рис. 1.4, а). Тому під час побудови сумарної нелінійної характеристики систему координат другої характеристики повертають на 90^°, з’єднуючи вісі і .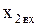

У першій чверті будують характеристику НЕ1, у другій – НЕ2, у третій проводять бісектрису, за допомогою якої у четвертій чверті отримують сумарну нелінійну характеристику (рис. 1.4, б).

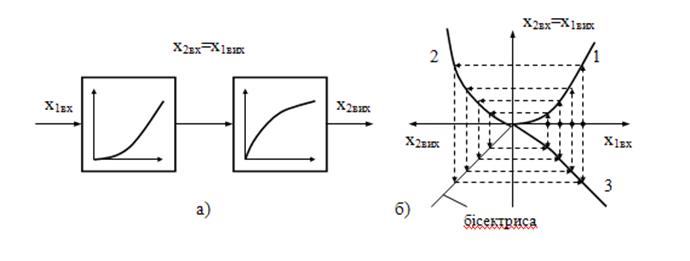
а) – структурна схема послідовного з’єднання нелінійних елементів;
б) – побудова сумарної (3) нелінійної характеристики при послідовному з’єднанні

Рисунок 1.4 – Послідовне з’єднання нелінійних елементів

Деякі типові нелінійності надані у блоці Nonlinear бібліотеки simulink пакета “Matlab” (рис. 1.5):

RateLimiter – обмеження швидкості; у блоці параметрів задається гранична швидкість зростання (risingslewrate) і гранична швидкість убування (fallingslewrate) вхідного сигналу;

Saturation – обмеження лінійності за виходом ( насичення); у блоці параметрів можна задавати значення верхнього (upperlimit) і нижнього (lowerlimit) обмеження;

DeadZone – зона нечутливості (мертва зона); у блоці параметрів можна задавати ширину зони нечутливості (startofdeadzone, endofdeadzone);

Relay – двопозиційне реле з гістерезисом; у блоці параметрів задають ширину петлі, указуючи моменти вмикання (switchonpoint) і вимикання (switchoffpoint) реле, а також величину сигналу при ввімкненому (outputwhenon) і вимкненому (outputwhenoff) реле; за допомогою цієї нелінійності можна змоделювати ідеальну релейну характеристику (рис. 1.2, в), якщо задати моменти вмикання і вимикання нульовими;

Backlash – люфт, або мертвий хід. Якщо різниця між вхідною й вихідною величиною менша за величину мертвого ходу, зміна вхідної величини не впливає на вихідну величину. У протилежному випадку вихідна величина повторює змінювання вхідної величини з різницею, що дорівнює величині мертвого ходу. У блоці параметрів можна задавати ширину люфту (deadbandwidth), а також початкове значення виходу (initialoutput);

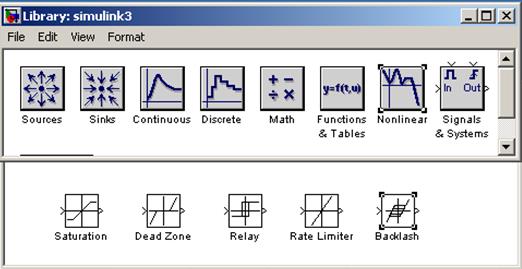
Рисунок 1.5 – Основні нелінійності бібліотеки simulink пакета “Matlab”

За допомогою комбінацій цих нелінійностей можна отримати й інші нелінійні елементи. Наприклад, послідовним з’єднанням елементів “Dead zone” і “Saturation” можна отримати статичну характеристику “Обмеження лінійності за виходом із зоною нечутливості” (рис. 1.6).

Дата добавления: 2015-10-24