Експериментальні методи настройки регулятора

Метод незгасаючих коливань. Для випадку, коли невідома передавальна функція системи, або аналітичний розрахунок регулятора являє собою складну задачу, синтез параметрів регулятора проводиться експериментальним шляхом за таким алгоритмом.

У працюючій системі вимикаються інтегральна і диференціальна складові регулятора (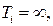 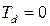), тобто система переводиться в П-закон регулювання.

Шляхом послідовного збільшення 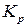з одночасною подачею невеликого стрибкоподібного сигналу задання добиваються виникнення в системі незгасаючих коливань з періодом 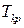. Це відповідає виведенню системи на межу коливальної стійкості. При виникненні даного режиму роботи фіксуються значення критичного коефіцієнта підсилення регулятора 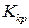і періоду критичних коливань у системі 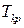. При появі критичних коливань жодна змінна системи не повинна виходити на рівень обмеження.

За значеннями 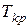і 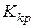розраховуються параметри настройки регулятора:

П-регулятор: ;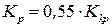

ПІ-регулятор: ; ;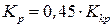

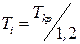ПІД-регулятор: ; ; .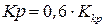

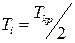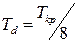Розрахунок настройок регулятора можна проводити за критичною частотою власне об'єкта керування 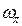. Ураховуючи, що власна частота 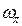ОУ збігається з критичною частотою коливань замкнутої системи з П-регулятором, величини 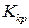і 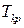можуть бути визначені за амплітудою і періодом критичних коливань власне об'єкта керування.

При виведенні замкнутої системи на межу коливальної стійкості амплітуда коливань може перевищити допустиме значення, що, у свою чергу, призведе до виникнення аварійної ситуації на об'єкті або до випуску бракованої продукції. Тому не всі системи керування промисловими об'єктами можуть виводиться на критичний режим роботи.

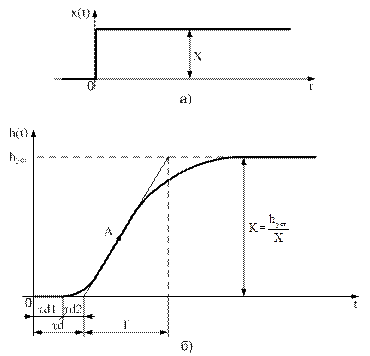
Рисунок 5.2 – Графіки вхідного сигналу (а), відгуку системи

та схема визначення динамічних характеристик (б)

У випадку, коли відома перехідна функція системи, синтез регулятора можна провести за розрахунковими формулами (табл. 5.1) з використанням характеристик перехідного процесу.

Для визначення динамічних характеристик перехідного процесу необхідно побудувати дотичну через точку перегину А.

Динамічний коефіцієнт підсилення – величина, що показує, у скільки разів дану ланку підсилює вхідний сигнал (у сталому режимі), і рівна відношенню величини технологічного параметра h_ust в сталому режимі до вхідної величини X:

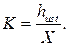
(5.18)

Стале значення вихідної величини h_ust – це значення h при t → ∞.

У системах автоматичного регулювання після отримання збурюючої дії регульований параметр змінюється не миттєво, а через деякий час. Цей час називається запізнюванням процесу в об'єкті. Розрізняють ємнісне і транспортне запізнювання. Ємнісне запізнювання залежить від ємності об'єкта регулювання. Транспортним (динамічним) запізнюванням називається проміжок часу від моменту зміни вхідної величини x до початку зміни вихідної величини h. Чим більше час повного запізнювання, тим важче регулювати такий процес.

Таблиця 5.1 – Формули для розрахунку регуляторів за відомими параметрами перехідного процесу

Регулятор	Типовий процес регулювання
Аперіодичний	з 20%-м перерегулюванням	Jmin
І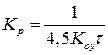
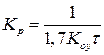
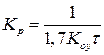
П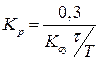
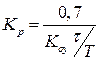
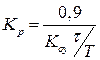
ПІ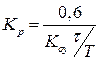
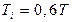
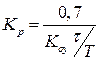
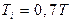
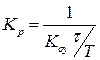
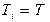
ПІД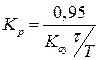

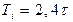
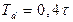
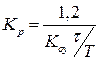
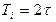
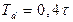
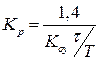
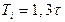
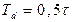
Стала часу об'єкта Т може бути визначена відповідно до рис. 5.2.

Метод використовується для швидкої, наближеної оцінки значень параметрів настройки регулятора для оптимальних типових процесів регулювання.

Передавальна функція регулятора має вигляд:

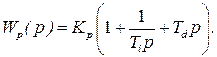
(5.19)

Синтез цифрового регулятора за аналоговим прототипом. Розглянемо процедуру синтезу алгоритму цифрового ПІД-регулятора з відповідного безперервного закону, що має вигляд

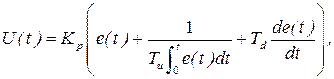(5.20)

де 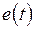– помилка регулювання.

Запишемо рівняння (5.20) у скінченних різницях шляхом заміни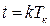

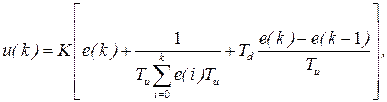(5.21)

де 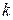=1, 2, 3...– номер періоду квантування, 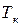– величина періоду квантування. Зазначимо, що при достатньо малих періодах квантування цифровий ПІД-закон керування забезпечує майже таку саму якість процесів керування, що і початковий безперервний закон (5.20). На практиці замість обчислень абсолютних значень керуючого сигналу зручніше обчислювати його прирощення 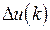на кожному такті. У цьому випадку стає можливим використовувати даний алгоритм для керування об'єктами з пропорційними та інтегруючими виконавчими механізмами. У результаті можна отримати так званий швидкісний алгоритм керування, повністю еквівалентний початковому

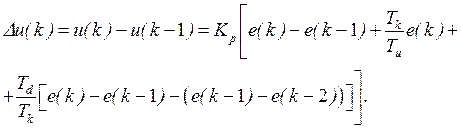(5.22)

Привівши подібні члени, отримаємо

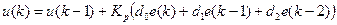(5.23)

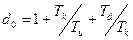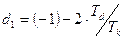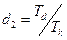, , (5.24)

Структурна схема цифрового ПІД-регулятора наведена на рис. 5.3.

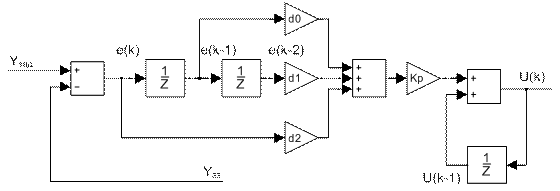
Рисунок 5.3 – Структурна схема швидкісного ПІД-регулятора

Вибір періоду квантування. Для того щоб ефект квантування за часом мало позначався на динаміці системи цифрового регулювання, рекомендується вибирати період квантування із співвідношення:

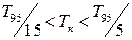(5.25)

де 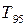– це час досягнення вихідним сигналом рівня 95 % від усталеного значення при подачі на вхід об'єкта ступінчастого сигналу.

Інший підхід до вибору величини періоду квантування базується на рекомендаціях американських учених Зіглера і Нікольса, згідно з якими:

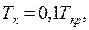(5.26)

де 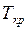– період критичних коливань об'єкту керування.

Не можна вибирати великі періоди квантування, особливо для відповідальних процесів, оскільки в цьому випадку аварійні ситуації ліквідовуватимуться дуже повільно. Водночас при дуже малому періоді квантування підвищуються вимоги до швидкодії ЕОМ і збільшується вплив шумів.

Дата добавления: 2015-10-24