
Читайте также:
|
Системы отсчета, в которых выполняется первый закон Ньютона, называются инерциальными.
Инерциальные системы - системы отсчета, относительно которых тела движутся с постоянной по модулю скоростью в отсутствии или компенсации внешних воздействий.
Специальная теория относительности (СТО) рассматривает явления, происходящие только в инерциальных системах отсчета.
СТО часто называется релятивистской теорией.
СТО предложена немецким физиком А.Эйнштейном (1905 г.) для согласования экспериментальных данных по измерению скорости света с теоретической базой классической (ньютоновской) механики.
Теория относительности базируется на двух постулатах. Справедливость постулатов доказывается тем, что следствия, вытекающие из постулатов, хорошо согласуются с результатами многочисленных экспериментов (например, движение элементарных частиц в ускорителях).
1 постулат (принцип относительности Эйнштейна) -при одних и тех же условиях все физические явления в любой инерциальной системе отсчета происходят совершенно одинаково.
Это значит, что никакими экспериментами (механическими, электромагнитными, оптическими и др.), поставленными внутри инерциальной системы, невозможно установить, покоится эта система или движется равномерно и прямолинейно.
Из данного постулата следует, что при переходе из одной инерциальной системы отсчета к другой математические выражения законов физики не должны изменяться.
2 постулат (принцип постоянства (инвариантности) скорости света) -скорость света в вакууме не зависит от скорости движения источников и приемников света и во всех инерциальных системах отсчета одинакова.
Из данного постулата следует, что взаимодействия между телами в природе не могут распространяться с бесконечно большой скоростью. Скорость света в вакууме является предельной скоростью передачи сигнала.
| Следствия постулатов теории относительности | |||
· относительность
расстояний

| ➨ 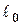 - длина стержня в неподвижной системе отсчета, относительно которой стержень покоится; - длина стержня в неподвижной системе отсчета, относительно которой стержень покоится;
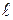 - длина стержня в подвижной системе отсчета, относительно которой стержень движется со скоростью - длина стержня в подвижной системе отсчета, относительно которой стержень движется со скоростью  .
Сокращение длины тем больше, чем больше скорость движения.
Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета. .
Сокращение длины тем больше, чем больше скорость движения.
Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета.
| ||
· относительность
промежутков времени
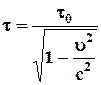
| ➨  - интервал времени между двумя событиями, происходящими в одной и той же точке неподвижной системы отсчета;
➨ - интервал времени между двумя событиями, происходящими в одной и той же точке неподвижной системы отсчета;
➨  - интервал между этими же событиями в подвижной системе отсчета, движущейся относительно неподвижной со скоростью - интервал между этими же событиями в подвижной системе отсчета, движущейся относительно неподвижной со скоростью  .
Длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
Таким образом, ход часов замедляется в системе отсчета, относительно которой часы движутся. .
Длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна.
Таким образом, ход часов замедляется в системе отсчета, относительно которой часы движутся.
| ||
· релятивистский закон сложения скоростей
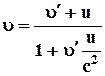
| ➨ 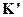 - подвижная система отсчета, которая движется со скоростью - подвижная система отсчета, которая движется со скоростью 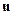 вдоль оси ОХ относительно неподвижной системы отсчета К.
➨точкаМдвижется со скоростью вдоль оси ОХ относительно неподвижной системы отсчета К.
➨точкаМдвижется со скоростью 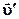 вдоль оси вдоль оси  подвижной системы подвижной системы 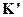 . .
| 
| |
Зависимость массы от скорости (релятивистская масса)

| ➨ 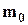 - масса покоящегося тела; масса покоя является величиной, одинаковой для всех систем отсчета, в которых тело покоится.
➨ - масса покоящегося тела; масса покоя является величиной, одинаковой для всех систем отсчета, в которых тело покоится.
➨ 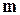 - масса того же тела, но движущегося со скоростью - масса того же тела, но движущегося со скоростью 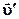 .
При увеличении скорости тела его масса .
При увеличении скорости тела его масса  возрастает. возрастает.
| ||
Релятивистский
импульс
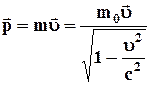
| ➨ релятивистский импульс пропорционален вектору скорости. | ||
| Закон сохранения релятивистского импульса | ➨ релятивистский импульс замкнутой системы сохраняется, т.е. не изменяется с течением времени. | ||
| Основной закон релятивистской | ➨ вектор результирующей силы  , приложенной к материальной точке (телу), равен изменению вектора релятивистского импульса , приложенной к материальной точке (телу), равен изменению вектора релятивистского импульса 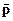 тела (или материальной точки) за единицу времени тела (или материальной точки) за единицу времени
| ||
| динамики | 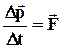
| ||
Связь между
массой и энергией

| ➨ полная энергия тела или системы тел равна произведению ее полной релятивистской массы на квадрат скорости света в вакууме. | ||
Энергия покоя

| ➨ энергия, которой обладает неподвижное тело; ➨ энергия покоя – это внутренняя энергия тела. | ||
| Кинетическая энергия тела | ➨ представляет собой разность между полной энергией тела  и энергией покоя и энергией покоя 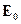

| ||
| 1.4 ЭЛЕМЕНТЫ МЕХАНИКИ ТВЕРДОГО ТЕЛА |
j Момент инерции тела относительно оси – физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси

Момент инерции тела при вращательном движении играет такую же роль, как масса при поступательном движении.
l Теорема Штейнера (используется для определения момента инерции твердого тела относительно произвольной оси):
момент инерции тела относительно любой оси вращения равен моменту его инерции  относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела m на квадрат расстоя- относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела m на квадрат расстоя-
|  С а С/
С а С/
|
ния а между осями 
|
k Кинетическая энергия вращающегося тела представляет собой алгебраическую сумму кинетических энергий отдельных его точек, т.е.


В случае, если тело движется поступательно со скоростью v и одновременно вращается вокруг некоторой оси с угловой скоростью 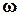 (например, катящееся колесо), то полная кинетическая энергия этого равна
(например, катящееся колесо), то полная кинетическая энергия этого равна

Дата добавления: 2015-09-04; просмотров: 131 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| K Основные законы вращательного движения | | | L Моменты инерции однородных тел правильной формы |