
Физическая система, совершающая колебания, называется осциллятором (лат. oscillo –качаюсь).
Гармонический осциллятор – осциллятор, совершающий гармонические колебания согласно уравнению:
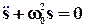 , (1)
, (1)
решение которого имеет вид:
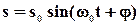 (2)
(2)
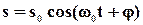 (3)
(3)
Классические осцилляторы – математический маятник, физический маятник.
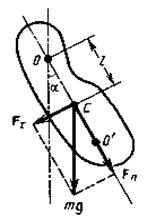 
| k Физический маятник –твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О подвеса, не проходящей через центр масс С тела.
Если маятник отклонен из положения равновесия на некоторый угол 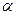 , то в соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы F можно записать в виде: , то в соответствии с уравнением динамики вращательного движения твердого тела момент М возвращающей силы F можно записать в виде:
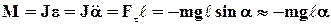 , (4) , (4)
|
где J – момент инерции маятника относительно оси, проходящей через
точку О;
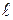 - расстояние между точкой подвеса и центром масс маятника;
- расстояние между точкой подвеса и центром масс маятника;
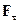 =-mgsin
=-mgsin 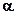
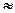 -mg
-mg 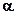 - возвращающая сила (знак минус обусловлен тем, что направления
- возвращающая сила (знак минус обусловлен тем, что направления 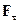 и
и 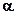 всегда противоположны;
всегда противоположны; 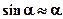 соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия).
соответствует малым колебаниям маятника, т.е. малым отклонениям маятника из положения равновесия).
Уравнение (4) можно записать в виде:
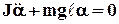 или
или 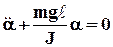
Принимая
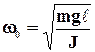 , (5)
, (5)
получим уравнение
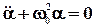 ,
,
решение которого имеет вид:
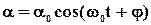 (6)
(6)
Из выражения (6) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой 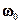 и периодом:
и периодом:
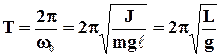 , (7)
, (7)
где 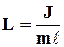 - приведенная длина физического маятника, т.е. длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
- приведенная длина физического маятника, т.е. длина такого математического маятника, период колебаний которого совпадает с периодом колебаний данного физического маятника.
Точка  на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качания физического маятника.
на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качания физического маятника.
Оборотный маятник – один из типов физического маятника.
Частным случаем физического является математический маятник, вся масса которого сосредоточена в одной точке – центре масс.
 Дата добавления: 2015-09-04; просмотров: 66 | Нарушение авторских прав
|