Читайте также:
|
Колебаниями называются движения или процессы, которые характеризуются повторяемостью во времени.
В зависимости от физической природы колебательного процесса и «механизма» его возбуждения различают колебания: механические (например, колебания маятников, струн, качка корабля, волнения моря и т.п.); электромагнитные; электромеханические.
Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса:
, (1)
где А – амплитуда - максимальное значение колеблющейся величины;
- фаза колебаний в момент времени t;
- начальная фаза колебаний в момент времени t=0, [φ]= рад;
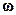- круговая (циклическая) частота – число полных колебаний, выраженных в радианной (угловой) мере, за 1 секунду.
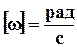
Период колебаний – промежуток времени, за который совершается одно полное колебание и фаза колебания получает приращение 
:
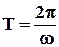
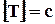
Частота колебаний – число полных колебаний за 1 секунду (величина, обратная периоду колебаний):
= 
Дифференциальное уравнение гармонических колебаний имеет вид:
, (2)
решением этого уравнения является выражение вида (1).
Дата добавления: 2015-09-04; просмотров: 105 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Осциллятор. | | | K Свободные затухающие колебания |