Одинаковой частоты

Пусть точка М одновременно колеблется вдоль осей координат ОХ и ОУ по законам:

,

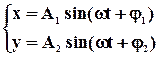где х и у – декартовы координаты точки М.

Уравнение траектории результирующего движения точки М в плос-кости ХОУ можно найти, исключив из выражений для х и у параметр t:

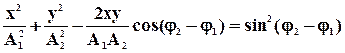
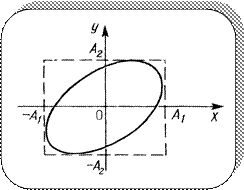
Траектория имеет форму эллипса, причем точка М описывает этот эллипс за время, равное периоду складываемых колебаний

.

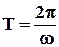Поэтому результирующее движение точки М называют эллиптически поляризованными колебаниями.

Ориентация осей эллипса и его размеры зависят от амплитуд складываемых колебаний А₁, А₂ и разности фаз :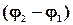

а) если 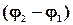= 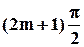(m=0,±1,±2,…), то оси эллипса совпадают с осями координат ОХ и ОУ, а размеры его полуосей равны амплитудам А₁ и А₂:

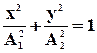
Если А₁ = А₂, тотраектория точки М представляет собой окружность, такое движение точки М называют циркулярно поляризованными или поляризованными по кругу.

б) если 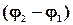= 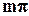(m=0,±1,±2,…), эллипс вырождается в отрезок прямой:

.

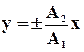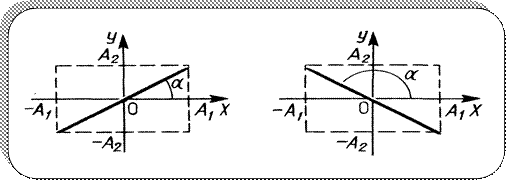
Знак «+» соответствует четным значениям 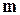, т.е. сложению синфазных колебаний; знак «-» - нечетным значениям 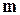, т.е. сложению колебаний, происходящих в противофазе.

В этих случаях точка М совершает линейно поляризованные колебания. Она колеблется с частотой складываемых колебаний и амплитудой:

,

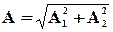вдоль прямой линии, составляющей с осью ОХ угол: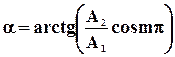

Если частоты взаимно перпендикулярных колебаний не одинаковы и относятся как целые числа, то траектории результирующего движения имеют более сложные формы. Их называют фигурами Лиссажу.

На рисунке представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху); разность фаз принимается равной .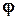

---

Дата добавления: 2015-09-04