
Читайте также:
|
Основываясь на рассмотренной операции сложения двух векторов, мы можем сложить три вектора и более. В этом случае складываются первые два вектора, к полученному результату прибавляется третий вектор, к получившемуся прибавляется четвертый и так далее.
Сложение нескольких векторов выполняется следующим построением. От произвольной точки А плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка B - это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор 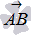 .
.
Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника. Приведем иллюстрацию правила многоугольника.
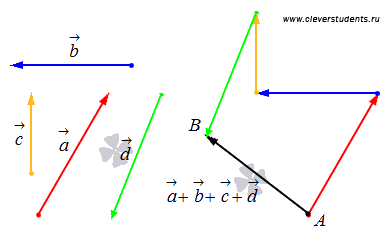
Абсолютно аналогично производится сложение нескольких векторов в пространстве.
К началу страницы
Дата добавления: 2015-08-27; просмотров: 167 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| II. Алгебраические дополнения | | | Операция умножения вектора на число. |