Свойства операций над векторами.

Итак, мы определили операцию сложения векторов и операцию умножения вектора на число. При этом для любых векторов и произвольных действительных чисел можно при помощи геометрических построений обосновать следующие свойства операций над векторами. Некоторые из них очевидны.

1. Свойство коммутативности .

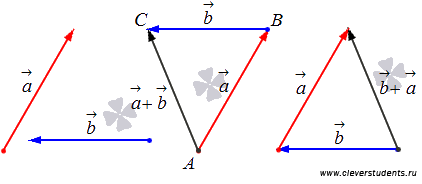
2. Свойство ассоциативности сложения .

3. Существует нейтральный элемент по сложению, которым является нулевой вектор , и . Это свойство очевидно.

4. Для любого ненулевого вектора 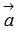существует противоположный вектор и верно равенство . Это свойство очевидно без иллюстрации.

5. Сочетательное свойство умножения . К примеру, растяжение вектора в 6 раз можно произвести, если сначала его растянуть вдвое и полученный вектор растянуть еще втрое. Аналогичного результата можно добиться, например, сжав вектор вдвое, а полученный вектор растянуть в 12 раз.

6. Первое распределительное свойство 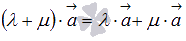. Это свойство достаточно очевидно.

7. Второе распределительное свойство . Это свойство справедливо в силу подобия треугольников, изображенных ниже.

8. Нейтральным числом по умножению является единица, то есть, . При умножении вектора на единицу с ним не производится никаких геометрических преобразований.

Рассмотренные свойства дают нам возможность преобразовывать векторные выражения.

Свойства коммутативности и ассоциативности операции сложения векторов позволяют складывать векторы в произвольном порядке.

Операции вычитания векторов как таковой нет, так как разность векторов 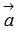и 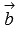есть сумма векторов 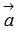и .

Учитывая рассмотренные свойства операций над векторами, мы можем в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования так же как и в числовых выражениях.

Разберем на примере.

Пример.

Упростите выражение, содержащее векторы .

Решение.

Если воспользоваться вторым распределительным свойством операции умножения вектора на число, то получим .

В силу сочетательного свойства умножения имеем .

Свойство коммутативности операции сложения векторов позволяет поменять местами второе и третье слагаемые , а по первому распределительному свойству имеем .

А теперь запишем кратко: .

Ответ:

.

17)Уравнение плоскости имеет вид: , где , , и – числовые коэффициенты.

Пусть нам нужно написать уравнение плоскости, которая проходит через точки , и

Так как точки принадлежат плоскости, то при подстановке их координат в уравнение плоскости, мы получим верные равенства.

Так как у нас три точки, мы должны получить систему из трех уравнений с четырьмя неизвестными. Примем коэффициент равным 1. Для этого разделим уравнение плоскости на . Получим:

Мы можем переписать это уравнение в виде: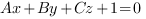

Внимание! Если плоскость проходит через начало координат, то d=0.

Чтобы найти коэффициенты А, В и С, подставим координаты точек , и в уравнение плоскости .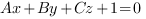

Получим систему уравнений:

Решив ее, мы найдем значения коэффициентов А, В и С.

18) Уравнение прямой в пространстве

Дата добавления: 2015-08-27