Вычитание и сложение операндов большой размерности

Если вы заметили, Команды сложения и вычитания работают с операндами фик­сированной размерности: 8, 16, 32 бит. А что делать, если нужно сложить числа большей размерности, например 48 бит, используя 16-разрядные операнды? К примеру, сложим два 48-разрядных числа (рис. 8.5):

1 слагаемое 0010001110010101 0100101111111000 1111111100110001 +

2 слагаемое 01QQ01Q010001011 1010010100100100 0100100110000110

1 шаг: сложение младших 16 бит ———————————————————> 10100100010110111

\

2 шаг сложение средних 16 бит -^-———> 01001011 11111000 /^^пазояд³^™
(с учетом переноса ^-^ + / н Р Н
из младшего разряда): ^* 1010010100100100 /,

11110001 00011100/

0000000000000001 '"'•' ' •' '. '^:ij

3 шаг-.сложение старших 16 бит ' ^11110001 °^0011101 ' ','., '/' ^.
(переноса из младшего - ' ''. -'. ' ^!'^*
разряда нет): -.
0010001110010101

+ ' ''•'"'•.

Q10001Q01QQQ1011 ______________ _______________

Результат сложения: 0110100000100000 11110001 00011101 0100100010110111
Рис. 8.5. Сложение операндов большой размерности

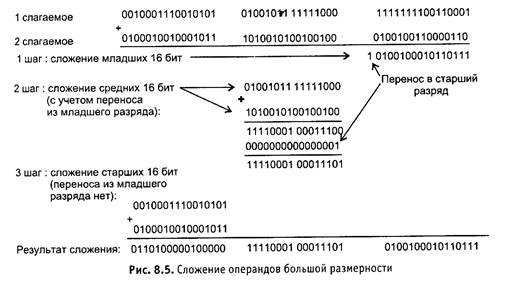
*iНa рис. 8.5 по шагам показана технология сложения длинных чисел. Видно, что Процесс сложения многобайтных чисел происходит так же, как и при сложении двух чисел «в столбик», — с осуществлением при необходимости переноса 1 isв старший разряд. Если нам удастся запрограммировать этот процесс, то мы ••.,. значительно расширим диапазон двоичных чисел, над которыми мы сможем вы­полнять операции сложения и вычитания.

Принцип вычитания чисел с диапазоном представления, превышающим стан­дартные разрядные сетки операндов, тот же, что и при сложении, то есть используется флат переноса cf. Нужно только представлять себе процесс вычи­тания в столбик и правильно комбинировать команды микропроцессора с коман­дой sbb. Чтобы написать достаточно интересную программу, моделирующую этот процесс, необходимо привлечь те конструкции языка ассемблера, которые мы еще не обсуждали. На прилагаемой к книге дискете в каталоге данного урока нахо­дятся исходные тексты подпрограмм, реализующих четыре основных арифмети­ческих действия для двоичных операндов произвольной размерности. Не поле­нитесь внимательно изучить их, так как они являются хорошей иллюстрацией к материалу, изучаемому на этом и последующих уроках. К этим примерам можно будет обратиться в полной мере после того, как будут изучены механизмы про­цедур и макрокоманд (уроки 10 и 13),

В завершение обсуждения команд сложения и вычитания отметим, что Кроме флагов cf и of в регистре eflags есть еще несколько флагов, которые можно ис­пользовать с двоичными арифметическими командами. Речь идет о следующих с]) флагах;

О zf -– флаг нуля, который устанавливается в 1, если результат операции равен О0, и в 0, если результат не равен 0;

О sf ---– флаг знака, значение которого после арифметических операций (и не только) совпадает со значением старшего бита результата, то есть с битом 7, 15 или 31. Таким образом, этот флаг можно использовать для операций над числами со знаком.

Дата добавления: 2015-08-27