
|
Читайте также: |
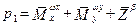 (6.5)
(6.5)
Из трех слагаемых наибольшим здесь является 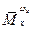 и в первом приближении можно принять
и в первом приближении можно принять  . Приближенное значение малого корня
. Приближенное значение малого корня 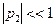 можно оценить, отбросив в (6.3) три первых слагаемых. Получим
можно оценить, отбросив в (6.3) три первых слагаемых. Получим
 . (6.6)
. (6.6)
Приближенные значения действительных корней можно найти методом последователь- ных приближений или любым другим способом.
Вычислив p1 и p2 по (6.4), определим p3,4:
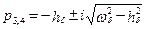 . (6.7)
. (6.7)
Из уравнений (6.3), (6.4) следует
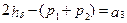 ; (6.8)
; (6.8)
 ,
,
откуда
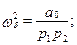
 . (6.9)
. (6.9)
В уравнении (6.3) для 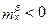 ,
,  при
при 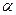 ≤
≤ 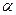 доп обычно
доп обычно  ,
, 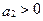 ,
, 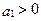 . Однако а0, характеризующий апериодическую устойчивость может быть как положительным, так и отрицательным. В соответствии с (6.8) при
. Однако а0, характеризующий апериодическую устойчивость может быть как положительным, так и отрицательным. В соответствии с (6.8) при 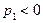 , корень p2 может иметь любой знак. При
, корень p2 может иметь любой знак. При  ВС будет медленно (т.к. корень маленький) отклоняться от исходного режима, развивая Δβ, Δωy, Δωx и Δγ по апериодическому закону. Медленный нарастающий крен Δγ(t) вызовет разворот и снижение ВС по пологой спирали. В связи с этим движение, соответствующее малому корню p2 = pсп, называется спиральным.
ВС будет медленно (т.к. корень маленький) отклоняться от исходного режима, развивая Δβ, Δωy, Δωx и Δγ по апериодическому закону. Медленный нарастающий крен Δγ(t) вызовет разворот и снижение ВС по пологой спирали. В связи с этим движение, соответствующее малому корню p2 = pсп, называется спиральным.
По критерию Рауса-Гурвица к условиям  ,
, 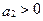 ,
, 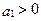 следует добавить
следует добавить

 , (6.10)
, (6.10)
которые представляют собой (при  ,
, 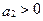 ,
, 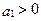 ) соответственно условия апериодической и колебательной устойчивости. Границами апериодической и колебательной устойчивости являются
) соответственно условия апериодической и колебательной устойчивости. Границами апериодической и колебательной устойчивости являются
 , где
, где
 .
.
При этом важное значение имеет соотношение величин 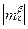 и
и 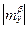 , которое приближено оценивается параметром æ
, которое приближено оценивается параметром æ  . Границы устойчивости можно нанести в координатах
. Границы устойчивости можно нанести в координатах  (см. рис. 35).
(см. рис. 35).

Для ВС, обладающего статической устойчивостью в путевом 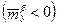 и поперечном
и поперечном 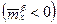 отношении при появлении скольжения будут возникать «восстанавливающие» моменты
отношении при появлении скольжения будут возникать «восстанавливающие» моменты 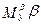 и
и  , уменьшающие скольжение и крен (возникший в результате скольжения).
, уменьшающие скольжение и крен (возникший в результате скольжения).
Пусть ВС накренилась вправо 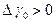 . В соответствии с (6.1) появится
. В соответствии с (6.1) появится  и пропорционально ему моменты
и пропорционально ему моменты 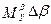 и
и  , под действием которых уменьшаются γ и β. Если
, под действием которых уменьшаются γ и β. Если  велика, то сначала произойдет уменьшение до нуля угла β, а угол крена не успеет обнулиться, т.е. останется величина
велика, то сначала произойдет уменьшение до нуля угла β, а угол крена не успеет обнулиться, т.е. останется величина 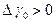 , т.к.
, т.к. 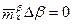 и отсутствует «восстанавливающий» момент по крену. Таким образом, при больших
и отсутствует «восстанавливающий» момент по крену. Таким образом, при больших  и малых
и малых  появляется остаточный крен, и движение будет происходить по спирали. Если наоборот,
появляется остаточный крен, и движение будет происходить по спирали. Если наоборот,  мала, то β будет уменьшаться медленно, а угол крена – быстро. В момент, когда крен станет нулевым, положительное β еще останется и ВС будет продолжать вращаться относительно OX. Левое полукрыло опускается. Появляется
мала, то β будет уменьшаться медленно, а угол крена – быстро. В момент, когда крен станет нулевым, положительное β еще останется и ВС будет продолжать вращаться относительно OX. Левое полукрыло опускается. Появляется 
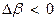 и благодаря моменту
и благодаря моменту  появится угловая скорость и крен в обратную сторону. Такое движение ВС называют «голландским шагом», имеющим форму «змейки». В виду того, что спиральное движение протекает относительно медленно (вяло) из-за малого значения p2 оно слабо ощущается пилотом, даже в случае некоторой спиральной неустойчивости. Что касается характеристик колебательного движения – оно должно быть обязательно устойчивым. (АП-25. 25.181).
появится угловая скорость и крен в обратную сторону. Такое движение ВС называют «голландским шагом», имеющим форму «змейки». В виду того, что спиральное движение протекает относительно медленно (вяло) из-за малого значения p2 оно слабо ощущается пилотом, даже в случае некоторой спиральной неустойчивости. Что касается характеристик колебательного движения – оно должно быть обязательно устойчивым. (АП-25. 25.181).
АП-25 25.177 d) В диапазоне скоростей от VMO/MMO–VFC/MFC максимальной эксплуатационной до максимальной скорости (М) для характеристик устойчивости допускается поперечная статическая неустойчивость, если неустойчивое движение развивается плавно, легко распознается и парируется пилотом. (отклонение элеронов обратное по знаку отклонения руля направления). В ранних НЛГС указывалось, что затухание боковых колебаний до 5% начальной амплитуды должно происходить не более чем за 12 секунд на взлетно-посадочных режимах и не более чем за 20 секунд на крейсерских режимах полета. Что касается спирального движения, при его неустойчивости допускается увеличение вдвое угла крена не менее чем за 20 секунд.
Лекция 10. 6.2.1 Устойчивость быстрого бокового движения
В (6.1), полагая cosα ≈ 1, sinα ≈ 0, δн/δэ = 0,  ;
;  =0 получаем две системы, которые можно изучать раздельно:
=0 получаем две системы, которые можно изучать раздельно:
 ;
;
 , (6.11)
, (6.11)
описывающую движение рыскания и
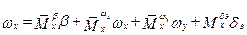 ;
;
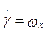 (6.12)
(6.12)
- движение крена. Причем система (6.11) может исследоваться независимо от (6.12), в свою очередь устойчивость системы (6.12) можно анализировать только по первому уравнению.
Характеристическое уравнение системы (6.11)
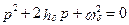 , (6.13)
, (6.13)
где: 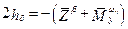 ;
; 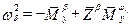 .
.
Корни этого уравнения комплексные и движение носит колебательный характер
 ;
;
 . (6.14)
. (6.14)
С учетом решения для β(t), характеристическое уравнение (6.12) имеет вид
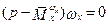 (6.15)
(6.15)
и решение его
 . (6.16)
. (6.16)
Изменение ωx в соответствии с (6.16), (6.12) и (6.14) будет следующим
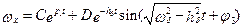 . (6.17)
. (6.17)
Устойчивость по критерию Рауса –Гурвица(при 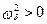 ) достигается при
) достигается при

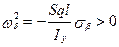 , (6.18)
, (6.18)
где
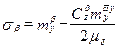 ; (6.19)
; (6.19)

 - относительная плотность ВС в боковом движении.
- относительная плотность ВС в боковом движении. 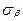 - называют степеньо статической устойчивости по каналу рыскания.
- называют степеньо статической устойчивости по каналу рыскания.
6.3Передаточные функции в боковом возмущенном движении
Изолированное движение рыскания. Из системы (6.12) после преобразования Лапласа получаем
 ; (6.20)
; (6.20)
где: 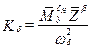 ;
; 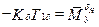 ;
; 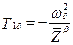 ;
;  ;
; 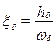 ;
;
hδ – декремент затухания углового движения в боковой плоскости;
ωδ – частота недемпфированных колебаний в боковом движении.
 . (6.21)
. (6.21)
Изолированное движение крена
В уравнениях (6.12) пренебрегаем составляющими  и
и  и после преобразования Лапласа получаем
и после преобразования Лапласа получаем
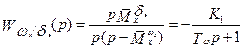 ; (6.22)
; (6.22)
где:  ;
; 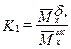 ;
;
 . (6.23)
. (6.23)
Из первого уравнения системы (6.1), предполагая 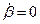 (угол
(угол  «установился»),
«установился»), 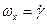 при
при
малых 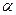 и
и  после преобразования Лапласа
после преобразования Лапласа
 . (6.24)
. (6.24)
Здесь
 , (см.(5.37));
, (см.(5.37)); 
Траекторное движение центра масс ВС. Будем предполагать, что ВС сбалансировано по моментам 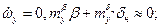 откуда
откуда

Примем, что: 
где
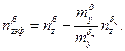 (6.25)
(6.25)
Рассмотрим уравнение для  системы (6.1)
системы (6.1)

Здесь выражение в скобках соответствует приближенно углу пути  , т.е. можно записать
, т.е. можно записать
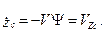
Продифференцируем это уравнение по времени 
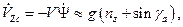
где приближенно  и соответствующая система уравнений возмущенного траекторного движения может быть представлена в следующем виде
и соответствующая система уравнений возмущенного траекторного движения может быть представлена в следующем виде


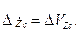 (6.26)
(6.26)
После преобразования Лапласа, определяются передаточные функции:
 ;
; 
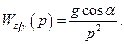 (6.27)
(6.27)
Рассмотрим основные передаточные функции в боковом возмущенном движении во взаимосвязи между собой

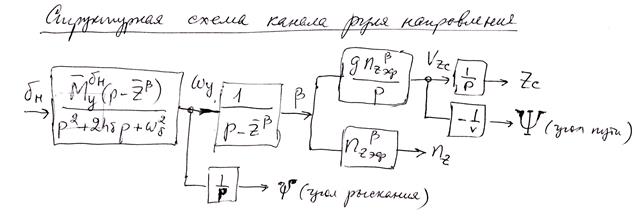
6.4. Анализ переходных процессов в боковом возмущенном движении.
6.4.1. Реакция ВС на отклонение элеронов
Для определения характеристик переходного процесса необходимо рассмотреть переда-
точную функцию  более общего вида, чем ранее. С этой целью в уравнении
более общего вида, чем ранее. С этой целью в уравнении
(см. систему (4.6)) для 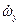 учитывается составляющая
учитывается составляющая 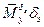 , и в итоге получаем
, и в итоге получаем
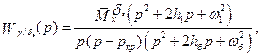 (6.28)
(6.28)
где  .
.
Характер переходных процессов по  определяется параметром
определяется параметром

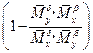
 (6.29)
(6.29)
и при 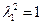 (
(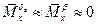 ) переходный процесс
) переходный процесс  имеет апериодический характер.
имеет апериодический характер.
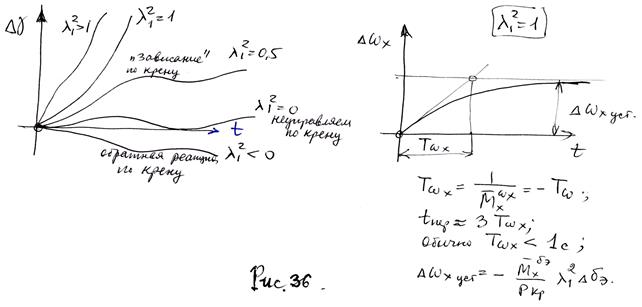
В этом случае передаточная функция принимает вид (6.23) На рис. 36 представлены переходные процессы по углу крена при различных значениях 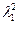 и
и 
6.4.2. Реакция ВС на отклонение руля направления
Передаточные функции, описывающие переходные процессы по  и
и  , с использованием полной системы (4.9) имеют вид:
, с использованием полной системы (4.9) имеют вид:
 ; (6.30)
; (6.30)
где:  ;
; 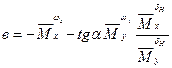 ;
;
 , (6.31)
, (6.31)
где 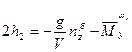 ;
;  и обычно обозначают
и обычно обозначают 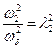 , который вычисляется по формуле (6.29) при замене в ней
, который вычисляется по формуле (6.29) при замене в ней 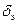 на
на  в выражениях производных. Характер переходного процесса по
в выражениях производных. Характер переходного процесса по  в зависимости от
в зависимости от 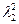 аналогичен тому, что показано на рис. 36. Переходный процесс по
аналогичен тому, что показано на рис. 36. Переходный процесс по 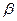 аналогичен графику переходной функции колебательного звена. Основные показатели переходных процессов рассчитываются так же, как показано в разделе (5.3.2.) при подставке вместо
аналогичен графику переходной функции колебательного звена. Основные показатели переходных процессов рассчитываются так же, как показано в разделе (5.3.2.) при подставке вместо  и
и 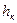 соответственно величин
соответственно величин  .
.
7. Особенности динамики пространственного движения
При движении в самом общем случае (нестационарные нелинейные режимы, сваливание, штопор и др.) учитываются четыре вида взаимодействия:
- кинематическое, обусловленное наличием 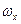 , т.к. при вращении ВС относительно ОХ производит циклическое изменение
, т.к. при вращении ВС относительно ОХ производит циклическое изменение 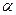 и
и 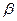 . Такое взаимодействие особенно ярко выраженное для спортивных и других маневренных самолетов.Для ВС – в меньшей степени.
. Такое взаимодействие особенно ярко выраженное для спортивных и других маневренных самолетов.Для ВС – в меньшей степени.
- аэродинамическое, определяемое влиянием 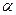 на аэродинамические характеристики бокового движения.
на аэродинамические характеристики бокового движения.
- гироскопическое, обусловленное появлением дополнительных гироскопических моментов, если ось вращения ротора ТРД или ТВД не совпадает с осью вращения ВС;
- инерционное, из-за появления дополнительных инерционных моментов, когда ось вращения ВС не совпадает ни с одной из главных осей инерции.
Поскольку ВС не является высоко маневренным самолетом, то наибольшее влияние из вышеперечисленных факторов в области нормальной эксплуатации ВС на динамику движения оказывают первые два. Вне области нормальной эксплуатации ВС (ошибки пилотирования, отказы в системе управления, особо интенсивные внешние возмущения и др.) весьма опасны так называемые критические режимы. Для современных самолетов наиболее характерны следующие критические формы движения: сваливание, штопор, аэроинерционное самовращение, срыв, самопроизвольное кренение. Два первых свойственны как дозвуковым, так и сверхзвуковым ВС И возникают из-за потери устойчивости и авторотации на больших околокритических и закритических углах атаки. Аэроинерционное самовращение (инерционное вращение) характерно для скоростных маневренных самолетов и возникает при превышении критической угловой скорости крена. Срыв самолета связан с потерей боковой (флюгерной) устойчивости и возникает, как правило, при превышении эксплуатационных чисел М полета. Самопроизвольное кренение возникает при превышении эксплуатационных значений индикаторной скорости Vi (скоростного напора) и связано с развитием упругих деформаций и часто с реверсом элеронов.
Рассмотрим несколько подробнее особенности сваливания и штопора.
7.1. Сваливание.
Сваливанием ВС называют непроизвольное быстро развивающееся движение со значи-тельной угловой скоростью и амплитудой, не парируемое летчиком, обусловленное потерей устойчивости на больших околокритических и критических углах атаки. Причины несим -метричных срывов на поверхности крыла: наличие  , конструктивной нежесткости. На рис.37 показано влияние
, конструктивной нежесткости. На рис.37 показано влияние  на величину угла атаки сваливания
на величину угла атаки сваливания 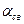 .
.
При полной симметрии срывов потока на верхней поверхности крыла, возможно, очень редко, симметричное сваливание на нос.
Виды сваливания:
1) сваливание на нос;
2) сваливание на крыло с пространственным апериодическим движением;
3) сваливание с резким разворотом по курсу с пространственным апериодическим движением;
4) сваливание с интенсивным кабрированием и пространственным апериодическим движением;
5) сваливание колебательное;
6) глубокое сваливание.
Лекция 11. 7.2. Авторотация
В начальный момент сваливания ВС приближается по углу атаки, близком к критическому, и при  при наличии
при наличии  вместо демпфирующих (тормозящих вращение) моментов крена и рыскания возникают авторотирующие (раскручивающие) моменты.
вместо демпфирующих (тормозящих вращение) моментов крена и рыскания возникают авторотирующие (раскручивающие) моменты.
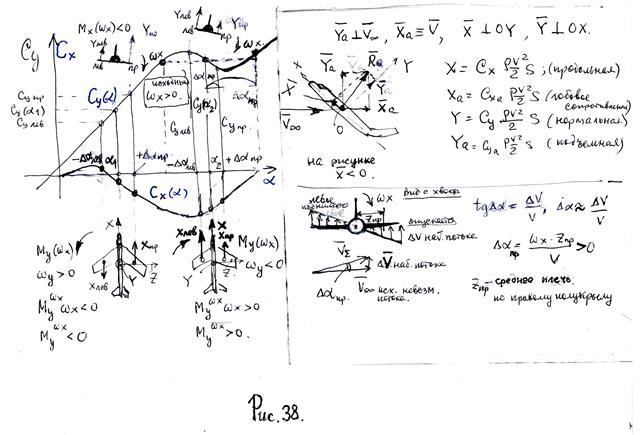
Рассмотрим движение при 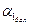 и
и  с угловой скоростью
с угловой скоростью  (правое полукрыло опускается). На опускающемся полу крыле всегда угол атаки увеличивается на величину
(правое полукрыло опускается). На опускающемся полу крыле всегда угол атаки увеличивается на величину  , при этом коэффициент нормальной силы до
, при этом коэффициент нормальной силы до  увеличивается, а при
увеличивается, а при  сначала уменьшается, а затем может снова увеличиваться в зависимости от величины
сначала уменьшается, а затем может снова увеличиваться в зависимости от величины  . На рис.38 при
. На рис.38 при 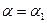 ,
, 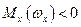
 и
и  , т.е.
, т.е. 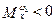 , следова-тельно, момент – демпфирующий. При
, следова-тельно, момент – демпфирующий. При  и малых
и малых  ,
, 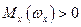 ,
,  , т.е.
, т.е.  и момент – авторотирующий; при этом же исходном
и момент – авторотирующий; при этом же исходном  и больших
и больших  может оказаться, что момент станет снова демпфирующим.
может оказаться, что момент станет снова демпфирующим. 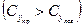 . В результате в зависимости от исходного
. В результате в зависимости от исходного  и значений
и значений 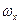 можно построить «диаграмму авторотации» (см. рис. 39).
можно построить «диаграмму авторотации» (см. рис. 39).
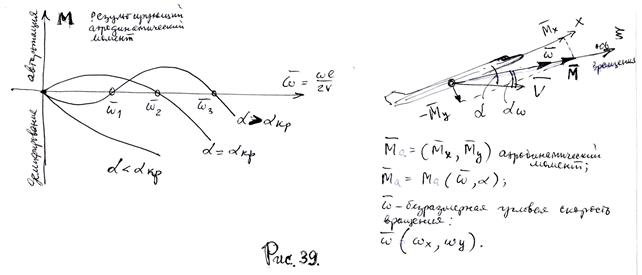
Установившееся вращение будет в точках 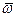
 ,
, 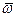
 ,
, 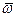
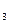 ; при этом, при
; при этом, при 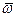 1 - будет неустойчивое вращение, а при
1 - будет неустойчивое вращение, а при 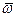
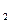 и
и 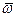
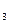 - устойчивые режимы вращения, что не трудно проверить по методу малых возмущений. Эту диаграмму можно перестроить в координатах
- устойчивые режимы вращения, что не трудно проверить по методу малых возмущений. Эту диаграмму можно перестроить в координатах  . В результате получаем зависимость
. В результате получаем зависимость 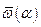 , в которой в диапазоне углов атаки от
, в которой в диапазоне углов атаки от  до
до  будут два режима установившейся авторотации; на меньших
будут два режима установившейся авторотации; на меньших  - неустойчивое вращения; при
- неустойчивое вращения; при  - больших – устойчивое вращение. Этот особый случай называется латентной (скрытой) авторотацией.
- больших – устойчивое вращение. Этот особый случай называется латентной (скрытой) авторотацией.

При изменении скольжения  происходит расширение/ сужение области неустановившейся авторотации.
происходит расширение/ сужение области неустановившейся авторотации.
7.3. Штопор
Авторотация ВС на закритических углах приводит к штопору. Этот режим наиболее опасный из всех критических режимов полета. В штопоре ВС совершает непроизвольное движение по крутой спирали траектории малого радиуса на режиме авторотации с одновременным вращением относительно трёх осей. При этом принимаются во внимание все виды взаимодействия (инерционное, кинематическое, аэродинамическое, гироскопическое). Рассмотрим влияние только одного из них – влияние инерционных моментов на режим движения в штопоре
Дата добавления: 2015-08-27; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Динамика продольного возмущенного движения ВС 2 страница | | | Динамика продольного возмущенного движения ВС 4 страница |