Аннотация. 2 страница

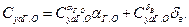(2.4)

Преобразуем выражение (2.3), учитывая (2.2), (2.4)

(2.5)

где обозначены: ;

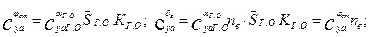
- коэффициент относительной эффективности руля высоты; 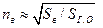при М<1, S_в – площадь руля высоты.

С целью дальнейшего упрощения выражения (2.5), установим соотношение между . При этом рассмотрим часть подъемной силы, зависящую только от угла атаки с учетом (2.2).

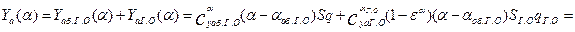
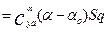
Откуда при 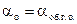, получаем

(2.6)

Преобразуем теперь составляющие (2.5), являющиеся множителями при α с учетом предыдущего соотношения

(2.7)

(с точностью до в предыдущем соотношении (2.7)).

Введем обозначения

(2.8)

тогда (2.7) преобразуется к виду

(2.9)

и коэффициент момента тангажа (2.5), с учетом (2.9), запишем в новой форме

(2.10)

где обозначены:

(2.11)

(2.12)

Учитывая, что можно (2.10) записать в другом виде

(2.13)

где

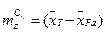(2.14)

При этом имеется в виду, что 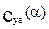зависит только от α при нулевых , а общая зависимость (в линейном диапазоне изменения ) имеет вид

(2.15)

при переменном . Если вместо руля высоты используется управляемый стабилизатор, то надо принять в (2.13) Примерная зависимость (2.13) для ВС нормальной схемы при М=const; имеет вид

2.2. Момент тангажа от тяги двигателя

В случае, когда двигатели расположены над фюзеляжем ВС или на пилонах под крыльями возникает дополнительный момент тангажа от тяги двигателей и в связи с тем, что этот момент зависит от угла атаки происходит одновременно смещение фокуса ВС по углу атаки. Рассмотрим лишь простые расчетные соотношения. Пусть турбореактивные двигатели (ТРД) располагаются на пилонах под крыльями

Момент тангажа возникает от двух сил: суммарный силы тяги от всех ТРД, и суммарной силы, возникающей из-за косой обдувки на входе воздушного потока в воздухозаборники. Последняя возникает, так как теряется часть количества движения секундной расходуемой массы воздуха в направлении перпендикулярном к оси двигателя. Её величина равна потерянному количеству движения в единицу времени:

где: 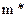- секундная масса воздуха (в кгс^-1)

Поскольку , где Va – скорость истечения отработанных газов из сопла двигателя, то выразив из последнего соотношения m*, после подстановки в Р_y, получаем

Суммарный момент тангажа, создаваемый всеми двигателями

или

.

Здесь <0, >0, i – число двигателей; qSb_A - дополнительный момент из-за смещения фокуса вперед (при переднем расположении двигателей)

(2.16)

где:

Коэффициент момента тангажа от всех двигателей с учетом смещения фокуса ВС будет следующий

(2.17)

Заметим, что аналогичные соотношения можно получить для ВС и с другими типами двигателей при различных их расположениях, Поскольку изменение момента тангажа от работы силовой установки обычно незначительное, то при качественном исследовании устойчивости и управляемости ВС будет часто пренебрегать этим эффектом и соответствующими составляющими в полном коэффициенте момента.

Лекция 3. 2.3. Дополнительные моменты тангажа в криволинейном неустановившемся полете

Неустановившееся движение ВС будет, когда кинематические параметры траектории, от которых зависят силы и моменты, действующие на ВС, будут переменными во времени. Это случай, когда , . При этом возникают дополнительные (по отношению к рассмотренным ранее) силы и моменты. Рассмотрим их последовательно(см рис.9).

Демпфирующий момент тангажа ВС складывается из демпфирующего момента крыла, ГО, фюзеляжа и других частей ВС. Основную часть при этом составляют поверхности, вынесенные от OZ связанной системы координат. Например, переднее и заднее ГО. Рассмотрим нормальную схему ВС с одним задним ГО. При вращении ВС с угловой скоростью на ГО набегает дополнительный воздушный ΔVго, обусловленный _z, т.е. и увеличивается угол атаки на величину

.

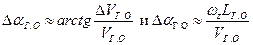Происходит прирост подъемной силы на ГО (см рис.10) в пределах . Заметим, что если , то произойдет уменьшение подъемной силы на ГО, т.к. при >0 может оказаться <0.

В пределах допустимых углов атаки на ГО возникает прирост подъемной силы

и продольный момент (учи-

тывая, что , )

, (2.18)

где - безразмерная угловая скорость тангажа ВС. Поделив (2.18) на qSb_A, получим коэффициент демпфирующего момента тангажа, вызванный ГО

(2.19)

где - обозначена частная производная коэффициента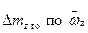

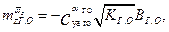(2.20)

где

Демпфирующие моменты остальных частей выводятся аналогично и здесь не приводятся. В итоге для суммарного демпфирующего момента тангажа ВС

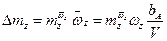, (2.21)

где

Момент тангажа, обусловленный запаздыванием скоса потока перед ГО.

Пусть ВС вращается так, что >0 За малое время воздушный поток достигнет ГО и угол атаки ГО за это время изменится и станет больше на величину . Из-за возникновения подъемной силы на крыле возникает скос потока за крылом, который с течением времени так же изменяется и скошенный поток достигает ГО не мгновенно, а с запаздыванием . В момент (t-τ) угол атаки крыла был меньше на величину 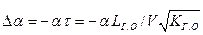, а скос потока в текущий момент времени t определяется кинематическими параметрами движения на момент времени t-τ ранее, т.е. также уменьшается на величину . Угол атаки ГО определяется как и уменьшение приводит к увеличению . Вследствие этого возникает дополнительная подъемная сила, направленная вверх против вращения

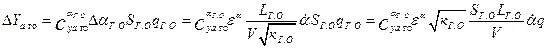
и дополнительно момент тангажа (где обозначено )

(2.22)

поделив на , получаем

, (2.23)

где .

2.4. Результирующий момент тангажа в неустановившемся криволинейном полете.

Суммируя (2.13), (2.17), (2.21) и (2.23) получим коэффициент момента тангажа для ВС нормальной схемы в неустановившемся полете ()

, (2.24)

где относительное положение фокуса ВС, с учетом изменения фокуса за счет тяги двигателей. При управляемом стабилизаторе надо принять ввести дополнительную составляющую продольного момента от лобового сопротивления ; если имеется переднее ГО, для него вводится дополнительная составляющая коэффициента момента, аналогично принятой для заднего ГО.

2.5. Продольная статическая устойчивость при фиксированном руле высоты.

При фиксированном руле высоты , примем за опорный режим полета( изменяется незначительно, ) при которых выполняется равенство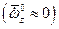

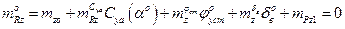
Это соотношение соответствует прямолинейному движению с 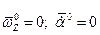(см. (2.24)). Верхним индексом «о» отмечен «опорный» (невозмущенный) режим полета. При малом изменении высоты полета можно для некоторой осредненной величины принять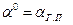

и зависимость представить в виде

с учетом «гипотезы стационарности» на основе которой принимается обозначенная зависимость от α (т.е. не зависит от и др.) можно считать, что при появлении 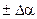по отношению к должно быть приращение . Приращение связано с изменением . Таким образом, если появляется «возмущение» 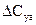в возмущенном движении (напомним, что в опорном: ), то это эквивалентно «возмущению» по перегрузке и наоборот. Рассмотрим теперь зависимость (см. рис. 12) для режима: .

В точках 1, 2, 3, 4, 5 возможны прямолинейные опорные режимы полета, для которых Примем, что соответствуют некоторым значениям В соответствии с определением статической устойчивости по выбранному параметру (см. раздел 1.1), которым у нас является , следует задать приращение по отношению к опорному и проверить будет ли ВС без участия пилота возвращаться к

опорному режиму полета. Зададим в точке 1 >0. Этому значению соответствует >0, при котором (см. рис. 12) появляется <0, уменьшающий (указано стрелкой вдоль оси абсцисс) и значит возвращающий ВС к исходному режиму полета. При <0 и соответственно <0, появляется >0, увеличивающий и, следовательно, , т.е. снова ВС возвращается к исходному опорному режиму полета. Аналогично можно проверить, что в точке 2 ВС не возвращается в исходный режим полета, а в точках 3, 4, 5 ничего сказать нельзя, т.к. приращение «в малом» отсутствует.

В возмущенном движении при появлении в точках соседних с 1 и 2, появляются моменты и даже при неизменном угле атаки появляется дополнительная угловая скорость и в результате получаем криволинейное движение.

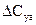Рассмотрим приращение в зависимости от (т.е. ) и в возмущенном криволинейном движении. У нас (т.к. ) и учитывая, что , получим . Из уравнения движения , предполагая неизменными величины 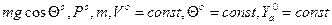опорных значений . Откуда 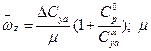- относи - тельная плотность ВС в продольном движении: ; .Приращение коэффициента момента тангажа в возмущенном криволинейном движении (по отношению к прямолинейному опорному: )(верхний индекс «о» здесь и далее опущен).

. (2.25)

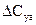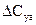Поделив левую и правую часть на и переходя к пределу , получим полную производную (т.к. зависит от непосредственно и от )

. (2.26)

Величину называют степенью продольной статической устойчивости по перегрузке при фиксированном руле высоты. Если мало по сравнению с , то можно принять

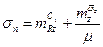(2.27)

где

По знаку можно судить о продольной статической устойчивости по перегрузке. Физический смысл «устойчивости по перегрузке» приведен в этом разделе выше с точностью до величины 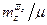, зависящей от демпфирующих свойств ВС и его плотности. В результате получаем: <0- устойчивое; >0- неустойчивое; - нейтральное опорное прямолинейное движение с V=const.

Продольная статическая устойчивость по скорости при фиксированном руле высоты. Исходным опорным (невозмущенным) движением является прямолинейный горизонтальный полет, снижение, подъем) полет с переменной скоростью , постоянной перегрузкой . Из-за движения с переменной скоростью происходит дисбаланс сил и следует изменять угол атаки (и соответственно силы 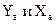) таким образом чтобы оставался постоянным угол Но, так как составляющая, зависящая от в выражении для мала, то главную роль в дисбалансе моментов и сил играет подъемная сила (Примем: Рассмотрим для определенности зависимость 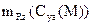на режиме разгона >0 в горизонтальном полете без крена 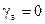и скольжения для различных чисел М. (рис.12). Здесь жирная линия соответствует условию горизонтального полета с разгоном от числа М=0,6 до М=1,3.

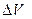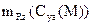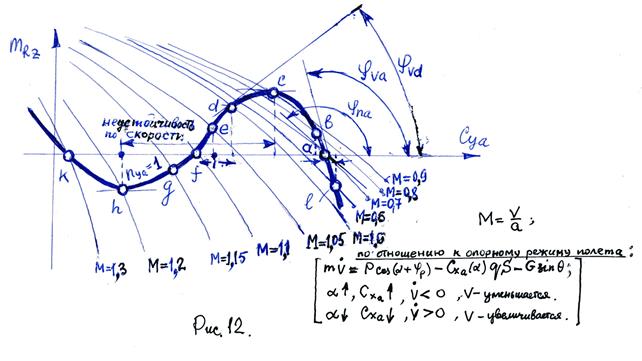
Пусть в точке «а» (расположенной на оси ) опорное движение происходит со скоростью, соответствующей М=0,7. В соответствии с определением статической устойчивости по параметру зададим возмущение по скорости <0, например, ΔМ < 0 и ΔМ= -0,1, что будет соответствовать точке «l» на зависимости . В этом случае величина такова, что момент направлен на уменьшение и будет возвращать ВС в исходный режим в точке «а». При «возмущении» по скорости ΔV > 0 и соответственно, например, ΔМ=+0,1, что будет соответствовать точке «в» при М=0,8.

Появляется 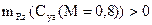, который приводит к увеличению и, следовательно, без вмешательства в управление пилота или автоматики возвращает ВС в исходный режим. Таким образом движение при М=0,7 в точке «а» будет статически

устойчивым по скорости.

Пусть теперь опорное движение происходит при М=1,05 в точке «е», где 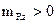. Зададим возмущение по скорости ΔV < 0 и, например, ΔМ= - 0,05. Тогда «возмущенное» движение будет происходить с положительным приращением 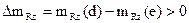, что приводит по отношению к опорному их увеличения до значений и соответственно дальнейшего уменьшения скорости и числа М. Аналогично можно показать, что при возмущении по скорости до числа М=1,1 будет происходить дальнейшее ее увеличение. Режим движения в точке «е» является статически неустойчивым по скорости. Нетрудно заметить, что диапазон неустойчивости по скорости будет от точки «с» до точки «h», т.е. от чисел М=0,9 до М=1,2. Напомним, что здесь приведены условные значения чисел М, хотя и близкие к действительным.

Показателем продольной статической устойчивости по скорости (здесь в горизонтальном полете) с фиксированным рулем высоты будет знак и величина полной производной 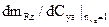, например, для точки «а»

В частности показатель продольной статической устойчивости по перегрузке (с точностью до 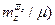будет

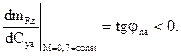
Степень продольной статической «неустойчивости» в точке «d» при М=1,05, соответственно

.

В точках «с» и «h» ВС будет «в малом» статически нейтральном по скорости (но только в отдельных точках).

В произвольном случае, когда степень продольной статической устойчивости по скорости определяется так же полной производной при опорном значении

. (2.28)

В случае горизонтального полета: и если приближенно принять

В горизонтальном полете

(2.29)

и если 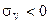, то ВС статически устойчиво по скорости, - неустойчиво, а при - статически нейтрально по скорости.

Дата добавления: 2015-08-27