
|
Читайте также: |
Конспект лекций написан на основе курса лекций, прочитанного студентам специальности 13.01.09. В курсе в основном рассматривается класс транспортных самолетов, которые будем называть «воздушными судами» (ВС) с дозвуковыми скоростями полета нормальной схемы. Предполагается, что на таких ВС установлена необратимая бустерная система управления (НБУ).
Основные определения и понятия устойчивости и управляемости используются для ВС, как жесткого тела без учета упругих колебаний крыла, фюзеляжа и других элементов конструкции.
Дается подробный анализ и исследование продольного движения ВС с выводом выражений для аэродинамических сил и моментов, балансировки, показателей устойчивости и управляемости, диапазона допустимых центровок. Приводится алгоритм выбора параметров горизонтального оперения. Для бокового движения принята та же схема изучения теоретического материала, но в упрощенном варианте без подробного вывода расчетных формул, с акцентом на особенности бокового движения, физические причины взаимосвязи «каналов» крена и рыскания.
Изучается динамика возмущенного движения с применением различных методов исследования. Устойчивость движения рассматривается с использованием теорем
А.М. Ляпунова об устойчивости по первому приближению. Характеристики управляемого движения ВС изучаются с помощью передаточных функций и частотных методов. Анализируется раздельно продольное и боковое возмущенные движения. Показывается особенность динамики пространственного движения, авторотации, режимов сваливания и штопора.
Рассматриваются: структура современной системы управления ВС, вопросы улучшения пилотажных характеристик и автоматического управления. Приведен обзор основных требований к летно-техническим и пилотажным характеристикам ВС.
Содержание
1. (Лекция1)Введение. Устойчивость и управляемость движения. Общие понятия ………………………………………………………………………………………….. 3 1.1. Виды устойчивости движения…………………………………………………………….. 5
1.2. Управляемость движения………………………………………………………………….7
2. (Лекция 2) Моменты, действующие на ВС в полете ……………………………………...8
2.1. Аэродинамический момент тангажа в установившемся прямолинейном полете……..9
2.2. Момент тангажа от тяги двигателей……………………………………………………..12
2.3. (Лекция 3) Дополнительные моменты тангажа в криволинейном неустановившемся полете……………………………………………………………………………………………. 13
2.4. Результирующий момент тангажа в криволинейном неустановившемся полете……..15
2.5. Продольная статическая устойчивость при фиксированном руле высоты……………16
2.6. (Лекция 4) Балансировка ВС и характеристики статической управляемости в продольном движении…………………………………………………………………………...20
2.6.1. Усилия на штурвале……………………………………………………………………21
2.6.2. Балансировка ВС в установившемся горизонтальном полете………………………22
2.6.3. Балансировка ВС в установившемся криволинейном полете в вертикальной плоскости …………………………………………………………………………………………23
2.6.4. Особенности продольной балансировки при взлете и посадке……………………. 25
2.6.5. Диапазон допустимых центровок и требования к выбору параметров горизонтального оперения……………………………………………………………………….26
3.(Лекция 5) Боковое движение.................................................................................................28
3.1. Аэродинамические моменты крена и рыскания……………………………………….. 28
3.2. Статическая устойчивость в боковом движении………………………………………..32
3.3. Балансировка ВС в установившемся боковом движении. Характеристики
поперечной и путевой статической управляемости…………………………………………….33
3.3.1. (Лекция 6) Усилия на рычагах управления элеронами и рулем направления в прямолинейном установившемся полете со скольжением…………………………………… 35
3.3.2. Балансировка с отказавшим двигателем……………………………………………..37
3.3.3. Балансировка ВС в установившемся криволинейном пространственном движении…………………………………………………………………………………………..39
4. (Лекция 7) Динамика возмущенного движения. Уравнения возмущенного движения ВС и методы их исследования …………………………………………………………………42
4.1.Математические методы исследования…………………………………………………..43
4.1.1. Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методом. Теоремы А.М. Ляпунова об устойчивости…….. 44
4.1.2. Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом……………………………………………………… 48
4.1.3. (Лекция 8) Исследование управляемого движения с помощью передаточных функций……………………………………………………………………………………………49
5. Динамика продольного возмущенного движения ВС ……………………………………50
5.1. Собственное продольное возмущенное движениеВС. Условия устойчивости
опорного движения………………………………………………………………………………..51 5.2. Выделение быстрой и медленной составляющих продольного возмущенного движения…………………………………………………………………………………………..52
5.2.1. Собственное продольное короткопериодическое возмущенное движениеВС. Условия устойчивости опорного движения…………………….………………………………52
5.2.2. Собственное продольное длиннопериодическое возмущенное движениеВС. Условия устойчивости опорного движения…………………….………………………………54
5.3. Реакция ВС в продольном движении на отклонение органов управления ………….56
5.3.1. Передаточные функции ВС в короткопериодическом возмущенном движении..56
5.3.2. (Лекция 9) Характеристики переходных процессов в короткопериодическом движении………………………………………………………………………………………….57
5.3.3. Передаточные функции возмущенного траекторного движения ВС в вертикальной плоскости(включая длиннопериодическое)…………………………………………………….60
6. Динамика бокового возмущенного движения ВС …………………………………….....62
6.1. Уравнения бокового возмущенного движения………………………………………….62
6.2. Устойчивость в боковом возмущенном движении…………………………………….63
6.2.1. (Лекция 10) Устойчивость быстрого бокового движения………………………...65
6.3. Передаточные функции ВС в боковом возмущенном движении………………………66
6.4. Анализ переходных процессов в боковом возмущенном движении…………………..68
6.4.1. Реакция ВС на отклонение элеронов…………………………………………………68
6.4.2. Реакция ВС на отклонение руля направления ………………………………………69
7.Особенности динамики пространственного движения …………………………………..69
7.1. Сваливание ВС……………………………………………………………………………70
7.2. (Лекция 11) Авторотация…………………………………………………………………70
7.3. Штопор……………………………………………………………………………………72
8. (Лекции12/13)Системы управления ВС …………………………………………………...74
8.1. Улучшение пилотажных характеристик в продольном движении……………………77
8.1.1. (Лекция 14) Демпфер тангажа………………………………………………………77
8.1.2. (Лекция 15) Автомат продольной устойчивости…………………………………..80
8.2. (Лекция 16) Автоматическое управление…………………………………………… 82
Приложение 1. Категории посадочных минимумов. Оценки пилотом технических показателей совершенства ВС. Требования к летно- техническим характеристикам ВС. Требования к пилотажным характеристикам ВС……………………………………………….83
Приложение 2. Частотные критерии устойчивости и нормирование запасов устойчивости.
Критерий Найквиста………………………………………………………………………………86
Литература......................................................................................................................................89
Вопросы к коллоквиуму по курсу «Устойчивость и управляемость транспортных воздушных судов» ……………………………………………………………………………………………...90
Лекция 1.Введение. Устойчивость и управляемость движения. Общие понятия. Проанализируем сначала «устойчивость положения», как частный случай движения в фик- сированный момент времени. Пусть на сечении рельефа местности, изображенном на рис.1, находятся идеальной формы шарики. Для проверки устойчивости используем
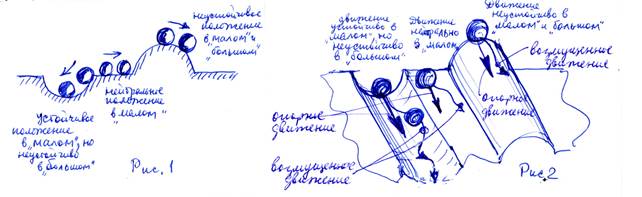
«принцип малых возмущений» при малых отклонениях от опорного (заданного) положения. На рис.2 с тем же рельефом принята не горизонтальная, а наклонная поверхность, а в качестве «опорного» - принято движение по средней (нижней) линии желобка слева, в средней части – положение произвольно, а справа примем за опорное (желаемое) движение по верхней части выпуклого желобка. Аналогично с помощью «метода малых возмущений» можно проверить будет ли движение устойчиво или нет. Характер возмущенного (в отклонениях от опорного) движения зависит от «кривизны» склонов выгнутого и выпуклого желобков.
1.1. Виды устойчивости движения. Под устойчивостью ВС понимается его способность без участия пилота сохранять заданный опорный (невозмущенный) режим полета и возвращаться к нему после непроизвольного отклонения под действием внешних возмущений, при условии прекращения действия возмущений. Различают устойчивость «в малом» и устойчивость «в большом» соответственно при малых (конечных) и больших возмущениях. Меру «малости» возмущений к сожалению не всегда можно указать заранее. Остановимся на этой проблеме в разделе линеаризации уравнений возмущенного движения. В зависимости от вида опорного движения рассматривают статическую устойчивость (обычно при балансировочном прямолинейном или криволинейном движении) и динамическую устойчивость при произвольном опорном режиме движения.
В соответствии с видом переходного процесса различают апериодическую и колебательную устойчивость. Если переходный процесс (возмущенное движение) в пределе совпадает с опорным (невозмущенным) по времени при  то устойчивость называют асимптотической. Иногда вводят понятие устойчивости на конечном отрезке времени. Важное место среди различных видов устойчивости занимает статическая устойчивость по выбранному параметру.
то устойчивость называют асимптотической. Иногда вводят понятие устойчивости на конечном отрезке времени. Важное место среди различных видов устойчивости занимает статическая устойчивость по выбранному параметру.
ВС будет статически устойчивым по выбранному параметру, если малое отклонение этого параметра (при всех остальных неизменных) от опорного значения сразу же приводит к появлению сил и/или моментов, направленных на уменьшение этого отклонения, после прекращения действия возмущений. Если силы и моменты направлены на увеличение этого отклонения, ВС – считается статически неустойчивым по этому выбранному параметру. В качестве параметра принимаются: коэффициент Cya, нормальная перегрузка nya, скорость V, угол атаки α, угол скольжения β и др. при их балансировочных значениях для опорного прямолинейного или криволинейного движения.
Для исследования динамической устойчивости (при возмущениях по начальным условиям), при построении систем автоматического управления широко применяют понятие устойчивости, предложенное академиком А.М. Ляпуновым (для краткости называют устойчивость по Ляпунову). Рассмотрим это понятие более подробно.
Предполагается, что движение исследуемой динамической системы описывается векторным дифференциальным уравнением (в форме Коши) вида


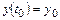 (начальное условие (н.у.)),
(начальное условие (н.у.)),
где y-n -мерный фазовый вектор, u-m -мерный вектор управления, f(·) – вещественная непрерывная вектор функция, удовлетворяющая условиям Липшица, 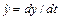 – производная по времени t. Пусть для некоторого ограниченного заданного закона управления uo(t), t ≥ t0, через начальное состояние
– производная по времени t. Пусть для некоторого ограниченного заданного закона управления uo(t), t ≥ t0, через начальное состояние  проходит невозмущенная (опорная, программная, исходная, желаемая) траектория
проходит невозмущенная (опорная, программная, исходная, желаемая) траектория 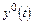 и она единственная в силу решения задачи Коши. Ставится задача об исследовании поведения невозмущенной траектории в случае, если начальное значение
и она единственная в силу решения задачи Коши. Ставится задача об исследовании поведения невозмущенной траектории в случае, если начальное значение  отличается от
отличается от 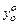 . (т.е. имеется «возмущение» по начальным условиям).
. (т.е. имеется «возмущение» по начальным условиям).
Невозмущенная траектория 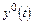 исходной системы называется устойчивой по Ляпунову, если для любого ε > 0 можно подобрать δ(ε,to) > 0 такое, что для всякого решения y(t) той же системы, начальное значение которого удовлетворяет неравенству
исходной системы называется устойчивой по Ляпунову, если для любого ε > 0 можно подобрать δ(ε,to) > 0 такое, что для всякого решения y(t) той же системы, начальное значение которого удовлетворяет неравенству
|| y(to) -  || < δ(ε,to)
|| < δ(ε,to)
для всех t ≥ to справедливо
||y(t,y(to),to,uo(t)) – yo(t,  ,to,uo(t))||<ε,
,to,uo(t))||<ε,
т.е. близкие по начальным значениям решения исходной системы остаются близкими для всех t ≥ to. Здесь под нормой ||y|| понимается 
Решение y(t,y(to),to,uo(t)), построенное для заданных начального условия y(to) и программного (опорного) управления uo(t) называется возмущенным и исследование устойчивости невозмущенного движения сводится к анализу свойств решений возмущенного движения. Для проверки свойств возмущенного движения целесообразно сделать замену переменных: 
и задача сводится к проверке на устойчивость тривиального решения  . Пример устойчивого тривиального условия при заданном
. Пример устойчивого тривиального условия при заданном  >0 изображен для одной из компонентов вектора
>0 изображен для одной из компонентов вектора  на рис. 3.
на рис. 3.
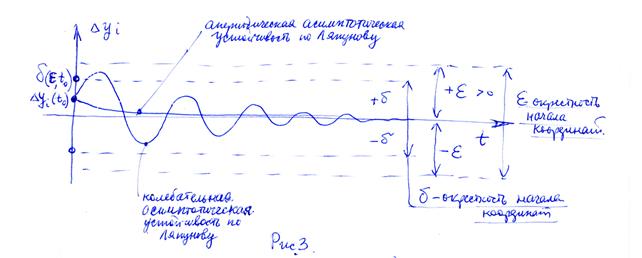
Если 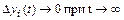 , то устойчивость будет асимптотической. Для случая двух компонент вектора
, то устойчивость будет асимптотической. Для случая двух компонент вектора  устойчивое движение изображено на рис. 4 для «возмущения»
устойчивое движение изображено на рис. 4 для «возмущения» 
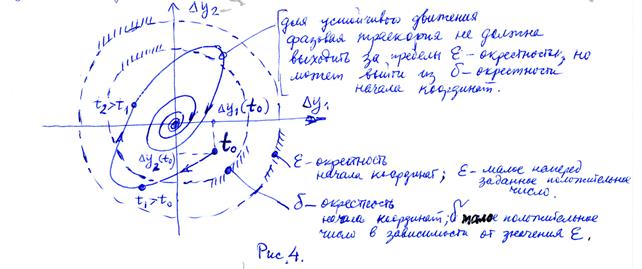
При определении динамической устойчивости в общем случае возможны возмущения более общего вида чем только отклонение по начальным условиям.
1.2. Управляемость движения.
Под управляемостью ВС понимается его способностью выполнять в ответ на целенаправленные действия пилота или автоматики любой, предусмотренный в процессе эксплуатации маневр (причем наиболее просто при минимальных затратах энергии пилота) в любых допустимых условиях полета, в том числе при наличии возмущений.
Управляемость различают: 1) продольную (относительно OZ) или по тангажу; 2) путевую (относительно OY) или по рысканию; 3) поперечную (относительно OX) или по крену.
В частности, в соответствии с основным определением, продольная управляемость – это свойство ВС переходить с одного продольного невозмущенного (опорного) движения (или режима полета) на другое по воле пилота при его воздействии на органы продольного управления: сектор газа и руль высоты.
Так же как и устойчивость, управляемость различают статическую и динамическую. Для пояснения статической управляемости целесообразно сначала дать определение балансировочных режимов полета.
Балансировочными называются режимы полета, в которых можно с достаточной степенью точности не учитывать в опорном движении, инерционную составляющую 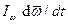 и считать действующие на ВС моменты «сбалансированными»:
и считать действующие на ВС моменты «сбалансированными»:  ,
, 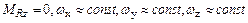 (в частности
(в частности  Отклонения органов управления для различных классов самолетов можно выделить следующие по крену: дифференциальное горизонтальное оперение (ГО), концевые рули, элевоны, элероны, флапероны, интерцепторы (спойлеры), поворотные концевые консоли крыла, руль направления, управляемое вертикальное оперение (ВО), струйные рули, управление вектором тяги, адаптивное крыло (дифференциальное изменение кривизны крыла); по курсу: руль направления, управляемое ВО, поворотный форкиль (гребень), струйные рули, управление передней стойкой шасси, расщепляющиеся рули, носовые рули, тормоза колес шасси; по тангажу: управляемое ГО (переднее, заднее), дифференциальное ГО, элевоны, струйные рули, управление вектором тяги, триммер, руль высоты.
Отклонения органов управления для различных классов самолетов можно выделить следующие по крену: дифференциальное горизонтальное оперение (ГО), концевые рули, элевоны, элероны, флапероны, интерцепторы (спойлеры), поворотные концевые консоли крыла, руль направления, управляемое вертикальное оперение (ВО), струйные рули, управление вектором тяги, адаптивное крыло (дифференциальное изменение кривизны крыла); по курсу: руль направления, управляемое ВО, поворотный форкиль (гребень), струйные рули, управление передней стойкой шасси, расщепляющиеся рули, носовые рули, тормоза колес шасси; по тангажу: управляемое ГО (переднее, заднее), дифференциальное ГО, элевоны, струйные рули, управление вектором тяги, триммер, руль высоты.
Потребные отклонения органов управления ВС для режима балансировки называются балансировочными.
Под статической управляемостью ВС принимается его способность выполнять в ответ на действия органов управления переход из заданного состояния балансировки в новое состояние балансировки бесконечно близкое к исходному. Оценить качественно статическую управляемость можно для заданного опорного режима полета по значениям потребных для балансировки ВС отклонениям органов управления, перемещениям рычагов управления (штурвала, рычага, управления двигателем и т.д.), усилиям на них и их производным по некоторым из параметров движения.
При оценке динамической управляемости рассматривается характер реакции ВС на отклонение органов управления от их балансировочных значений при переходе от заданного балансировочного режима полета к другому произвольному с учетом возмущений и переходного движения.
Лекция 2. 2. Моменты, действующие на ВС в полете
Результирующий момент 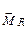 складывается из аэродинамического
складывается из аэродинамического 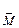 и момента тяги
и момента тяги  В проекциях на связанные оси координат
В проекциях на связанные оси координат  может быть представлен следующим образом
может быть представлен следующим образом
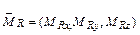 ,
,
где 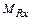 - момент крена;
- момент крена; 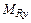 - момент рыскания;
- момент рыскания; 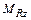 - момент тангажа.
- момент тангажа.
При этом определяются знаки моментов и соответствующих угловых скоростей вращения ВС по правилу «винта» (по часовой стрелке – положительно, если смотреть из начала координат, обычно расположенных в центре тяжести (ЦТ) или центре масс (ЦМ) ВС.
Правила знаков простейших органов управления показаны на рис. 5.

Обозначения: угловая скорость крена  x, рыскания
x, рыскания  y – и тангажа –
y – и тангажа –  z, отклонения управляющих органов: руля высоты
z, отклонения управляющих органов: руля высоты  , управляемого (перестановочного) стабилизатора
, управляемого (перестановочного) стабилизатора  , руля направления
, руля направления 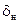 , элеронов обычных (концевых)
, элеронов обычных (концевых)  , элеронов корневых
, элеронов корневых  , элевонов
, элевонов  , закрылков
, закрылков  , щелевых интерцепторов: корневого левого
, щелевых интерцепторов: корневого левого 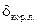 ; среднего левого
; среднего левого 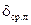 ; корневого правого
; корневого правого  ; соответственно в/н для верхних и нижних. В случае дифференциального отклонения каких-либо органов управления значения их углов указываются раздельно для правых и левых. На рис 5. знаком + указаны положительные значения углов, угловых скоростей, моментов, перемещений, усилий.
; соответственно в/н для верхних и нижних. В случае дифференциального отклонения каких-либо органов управления значения их углов указываются раздельно для правых и левых. На рис 5. знаком + указаны положительные значения углов, угловых скоростей, моментов, перемещений, усилий.
2.1. Аэродинамический момент тангажа в установившемся прямолинейном полете.
Выделяя основные составляющие, момент Мz удобно представить как алгебраическую сумму аэродинамических моментов тангажа ВС без ГО  момента ГО
момента ГО  (при нейтральном положении органов управления
(при нейтральном положении органов управления  ) и управляющих моментов ВС
) и управляющих моментов ВС 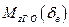 :
:
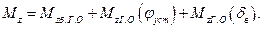
Второй из перечисленных моментов тангажа в зависимости от угла установки стабилизатора -  , фактически также является управляющим и может быть объединен с последним.
, фактически также является управляющим и может быть объединен с последним.
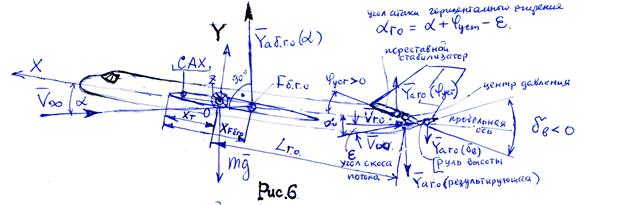
Рассмотрим аэродинамический момент тангажа в установившемся (V=const) прямолинейном (θ=const) полете без крена ( =0) и скольжения (β=0).
=0) и скольжения (β=0).
Для ВС нормальной схемы (см. рис.6), условно в прямолинейном полете близком к горизонтальному (Н ≈ const, 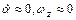 ) показаны аэродинамические силы (за исключением Ха), которые создают основной момент относительно ОZ. Подъемная сила всех частей ВС за исключением ГО
) показаны аэродинамические силы (за исключением Ха), которые создают основной момент относительно ОZ. Подъемная сила всех частей ВС за исключением ГО 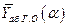 , зависящая от угла атаки (кроме
, зависящая от угла атаки (кроме 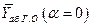 )приложена в фокусе ВС без ГО (обозначен
)приложена в фокусе ВС без ГО (обозначен  ).
).
Под фокусом по углу атаки будем понимать точку пересечения линии действия полной
аэродинамической силы 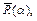 зависящей только от угла атаки, с продольной осью ВС.
зависящей только от угла атаки, с продольной осью ВС.
В частности вместо составляющей полной аэродинамической силы с некоторой погрешностью можно принять составляющую подъемной силы, зависящей от угла атаки.
Если ось OZ поместить в эту точку и вычислить продольный момент 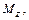 то в силу равенства нулю плеча действия сил, зависящих от
то в силу равенства нулю плеча действия сил, зависящих от 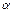 , производная момента
, производная момента 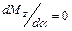 при всех осталь-
при всех осталь-
ных фиксированных параметрах:  и т.д.
и т.д.
Так же как и аэродинамические силы по принципу суперпозиции складываются из сил,
действующих на отдельные части ВС (крыло, фюзеляж и др.) так и фокус (для краткости «по углу атаки» будем опускать) зависит от фокуса крыла, фюзеляжа и др. Поэтому можно считать, что подъемная сила всех частей ВС без ГО 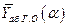 приложена в фокусе всех частей ВС без ГО. При этом полная подъемная сила (для статически устойчивого ВС)
приложена в фокусе всех частей ВС без ГО. При этом полная подъемная сила (для статически устойчивого ВС)

Здесь отметим, что аналогично можно ввести понятия фокуса по отклонению руля высоты,
закрылков и др. отклоняемых органов управления при малых их отклонениях и фиксированных остальных параметрах (углах).
Аэродинамический момент тангажа ВС запишем в следующем виде
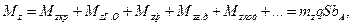
где 
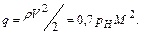
Здесь индексами обозначены составляющие момента тангажа: «кр»- от крыла; «ГО»-от горизонтального оперения; «ф»- от фюзеляжа; « »-от гондол двигателей; «подв»- от различных подвесок. Можно обозначить Мz от всех частей кроме ГО как
»-от гондол двигателей; «подв»- от различных подвесок. Можно обозначить Мz от всех частей кроме ГО как 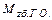 , а момент от стабилизатора и руля высоты
, а момент от стабилизатора и руля высоты  .
.
Из рис.6. видно, что для сбалансированных режимов полета момент от всех частей без ГО 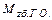 <0 (на пикирование) должен уравновешиваться моментом, создаваемым ГО,
<0 (на пикирование) должен уравновешиваться моментом, создаваемым ГО,  >0 (на кабрирование). При этом результирующая подъемная сила
>0 (на кабрирование). При этом результирующая подъемная сила  направляется вниз при отрицательном отклонении руля высоты
направляется вниз при отрицательном отклонении руля высоты  < 0 (задняя кромка - вверх) и тогда суммарная подъемная сила, которая в основном уравновешивает силу тяжести
< 0 (задняя кромка - вверх) и тогда суммарная подъемная сила, которая в основном уравновешивает силу тяжести 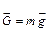 (например, в горизонтальном полете) определяется в виде разности сил
(например, в горизонтальном полете) определяется в виде разности сил 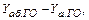 , что является невыгодным с точки зрения создания полной подъемной силы и этот случай кратко называют «потерей на балансировку».
, что является невыгодным с точки зрения создания полной подъемной силы и этот случай кратко называют «потерей на балансировку».
При малых углах атаки, полагая приближенно  и
и 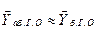 можно записать выражение для момента тангажа (см. рис. 6)
можно записать выражение для момента тангажа (см. рис. 6)
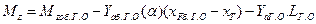 , (2.1)
, (2.1)
где: 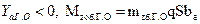 - момент тангажа ВС без ГО при α = 0;
- момент тангажа ВС без ГО при α = 0;  ;
;  - угол атаки горизонтального оперения, ε – скос потока в области ГО, приближенно зависящий от α и Сyaб.г.о. линейно:
- угол атаки горизонтального оперения, ε – скос потока в области ГО, приближенно зависящий от α и Сyaб.г.о. линейно:
 .
.
Подставив это соотношение в выражение для αг.о., получаем (прибавляя и вычитая αоб.г.о.)
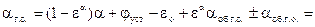
= 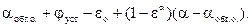 (2.2)
(2.2)
Преобразуем (2.1), принимая во внимание (2.2), выражения для  и поделив на qSbA
и поделив на qSbA
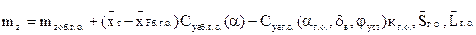 , (2.3)
, (2.3)
где:  коэффициент торможения потока у ГО,
коэффициент торможения потока у ГО,  ;
; 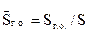 - относительная площадь ГО;
- относительная площадь ГО; 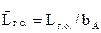 - относительное плечо ГО;
- относительное плечо ГО; 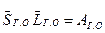 - относительный статический момент площади ГО; полагая малой величину
- относительный статический момент площади ГО; полагая малой величину 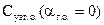 , коэффициент
, коэффициент 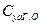 представим в виде
представим в виде 
Дата добавления: 2015-08-27; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Направления и проблемы реализации международных стандартов обращения с осужденными в уголовно-исполнительном российском законодательстве | | | Аннотация. 2 страница |