Аннотация. 5 страница

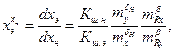(3.17)

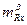
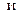
где 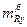- выбираются при фиксированных рычагах управления, а 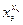- называют коэффициентом гармоничности управления, являющимся одним из показателей статической управляемости.

Во всем диапазоне максимальные усилия не должны превышать физических возможностей пилота .

3.3.2 Балансировка с отказавшим двигателем

Особо опасным является движение при выполнении разворота в сторону отказавшего двигателя, т.к. в этом случае пилоту значительно труднее быстро определить отказ. Рассмотрим балансировку ВС в прямолинейном установившемся полете с несимметричной тягой (Рис.29).

Например, при отказе (выключении) левого двигателя возникают дополнительные силы: - сила дополнительного лобового сопротивления отказавшего двигателя; - приращение поперечной силы вертикального оперения, обусловленного скосом потока из-за влияния несимметричности струй двигателей. Дополнительные моменты и силы в проекциях на оси OXYZ равны

,

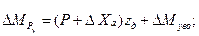
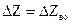где принято: обусловлены силой .

Переходя к коэффициентам сил и моментов, и принимая получим

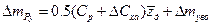
(3.18)

Имея в виду (3.5), с точностью до 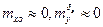, учитывая (3.18), получим условия балансировки с отказавшим одним двигателем

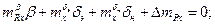
(3.19)

.

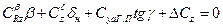Потребные для балансировки ВС углы принимая во внимание (3.6)÷(3.8), следующие:

; (3.20)

.

По этим формулам можно построить балансировочные зависимости потребных отклонений в прямолинейном полете с одним отказавшим двигателем (рис.30) в зависимости от .

Из всех возможных режимов прямолинейного установившегося полета можно выделить три.

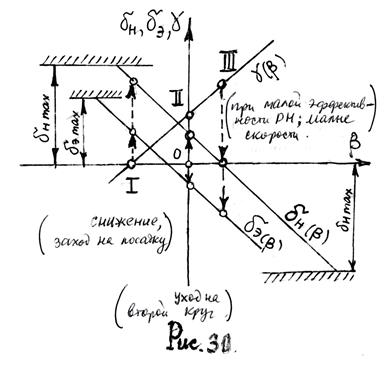
Полет без крена (режим I на зависимости 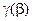, стрелками указаны потребные отклонения для балансировки). Этот режим с точки зрения «комфорта» экипажа и пассажиров наиболее приемлем. Но при этом потребные 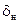и усилия на педалях близки к предельным, а скольжение 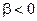происходит в сторону отказавшего левого двигателя.

Полет без скольжения (режим II), при котором получается меньшая величина лобового сопротивления и требуется меньшая потребная тяга работающего двигателя, но крен при этом в сторону работающего двигателя может быть значительным.

Полет с креном и скольжением (режим III) на полукрыло с работающим двигателем с малыми потребными , но слишком большими .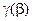

Выбор того или иного способа балансировки ВС зависит от запаса тяги двигателей и эффективности руля направления и его триммера.

3.3.3. Балансировка ВС в установившемся криволинейном пространственном

движении

В установившемся криволинейном полете появляются дополнительные моменты, обусловленные вращением ВС относительно связанных осей OX, OY и OZ, которые должны быть уравновешены дополнительным отклонением органов управления креном, рысканием и тангажом. Рассмотрим в качестве примера «правильный вираж» (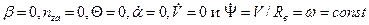). Угловая скорость поворота траектории (вдоль 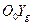нормальной системы координат) имеет компоненты 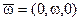и в соответствии с таблицей направляющих конусов

Условия балансировки при принятых допущениях (см. (3.3), (3.4) и (2.24))

;

;

где

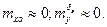
Их этой системы потребные для правильного виража будут следующие (3.21) ; (3.22)

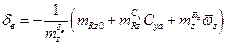, (3.23)

где

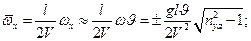
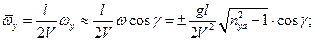
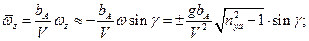
Характеристики (показатели) боковой статической управляемости ВС в установившемся криволинейном движении

Для их определения принято рассматривать установившееся изолированное движение крена, вызванное и 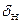, а также установившееся изолированное движении рыскания, вызванное 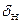. При таком подходе получаются приближенные условные показатели, не полностью отражающие фактическую управляемость, но оценивающую её удовлетворительно.

Примем в (3.3) ; ; ; , то равновесие момента будет при условии

.

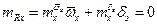Отсюда или

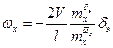(3.24)

и после дифференцирования

, (3,25)

где принимается при фиксированном значении .

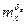Для нормального управления требуется . Эта производная характеризуется эффективностью элерона в движении крена. Знак зависит от знака . При некоторой критической скорости полета и недостаточной жёсткости конструкции крыла на кручение, элероны могут потерять полную эффективность ( 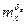=0). При скорости большей критической наступает реверс элеронов ( 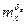>0), который недопустим для пилотирования ВС.

Производная ,характеризующая потребную величину отклонения штурвала (ручки) для создания 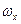= при и может быть вычислена по формуле (с учетом (3.24))

(3.26)

При использование демпфера крена должна быть определена с учетом его работы. Производная называется коэффициентом расхода штурвала на угловою скорость крена.

Усилия на ручке управления, потребные для создания единицы угловой скорости крена при и оцениваются производной для ВС с НБУ

, (3.27)

где - характеристика загрузочного механизма и принимается с учетом работы демпфера.

Показатели поперечной статической управляемости (3.26), (3.27) , 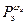должны быть отрицательными, а чтобы управление ВС не было слишком «тяжелым» или «строгим», их величина не должна выходить за определённые пределы.

При анализе установившегося вращения по крену, вызванному , можно аналогично получить коэффициенты расхода усилия и педалей на условия скорости крена

; ,

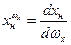которые также являются показателями боковой статической управляемости

Ограничимся определением установившегося значения угловой скорости крена при отклонении руля направления на угол и её производной по . Полагая (в целях упрощения анализа) в формулах (3.3) (3.5) (; ; ; )

(3.28)

Из этой системы найдем

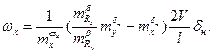(3.29)

Дифференцируя по , получим

(3.30)

Эта производная характеризует реакцию ВС на отклонение руля направления. При 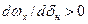будет прямая привычная реакция для пилота, а при (<0) – обратная реакция по крену на отклонение руля направления.

Обратная реакция может наблюдаться при 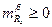в области (М 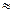0,8-1,2) и при малых углах атаки, когда ô ô-малы.

В качестве показателей путевой статической управляемости принимаются коэффициенты расхода усилий педали на угловую скорость рыскания и при М=const.

Имеются и другие показатели статической управляемости.

АП-25.25.147. Путевая и поперечная управляемость.

Должна иметь возможность при нулевом крене совершать разворот в сторону работающего двигателя и безопасно выполнять достаточно разное изменение курса до в направлении критического неработающего двигателя.

Для самолетов с четырьмя или более двигателями должны выполняться виражи с креном в сторону неработающих или противоположную неработающим двигателям из режима установившегося полета при скорости 1,4 (1,4 скорости сваливания или установившегося полёта)

При работе всех двигателей реакция самолета по крену должна быть достаточной для выполнения обычных манёвров.

(А) Эффективность поперечного управления должна обеспечивать вывод самолета из установившегося разворота с креном (при отклонении только штурвала по крену не более чем на ) за время не более 7с на режимах; взлета, (При безопасной скорости ); заход на посадку (на скорости захода на посадку со всеми работающими двигателями ); на крейсерских режимах и режимах набора высоты и снижения.

(с) Характеристики переходных процессов при отказе критического двигателя и невмешательстве пилота в управление в течение 5с после отказа должны быть такими, чтобы исключался выход самолета за эксплуатационные ограничения по 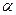, и 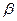и чтобы был .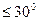

25.143. Приделы «Физической силы пилота» не должны превышать значения таблицы 1

Сила, прикладываемая пилотом к штурвалу или педалям, кг	Тангаж	Крен	Рыскание
Кратковременное усилие	35,0	27,0	70,0
Продолжительное усилие	4,5	2,50	9,0

25.177. На всех режимах полета должна соблюдаться боковая устойчивость. Допускается поперечная статическая неустойчивость, если неустойчивое движение развивается плавно, легко распознаётся и парируется пилотом (отклонение элеронов по знаку отклонению руля направления).

Лекция 7. 4. Динамика возмущенного движения. Уравнения возмущенного движения ВС и методы их исследования

Собирая вместе динамические и кинематические уравнения движения ВС, как материальные точки, и его вращательные движения вокруг центра масс (тяжести), Обозначим их в виде системы нелинейных дифференциальных уравнений

, (4.1)

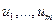здесь -фазовые переменные; - управляющие воздействия на ВС, 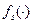-нелинейные функции соответствующих аргументов. Фазовыми переменными являются: (15 переменных). Управляющие воздействия: и т.д.; t-независимая переменная, чаше всего-время; - начальные условия (Н.У) при .

Пусть для заданных существует опорная (невозмущенная, программная) траектория движения ВС (рис.31)

Полагаем, что на движение ВС оказывают воздействие «возмущения»: ∆ ∆ , ветер, отклонение тяги двигателей от расчетных ∆Р и т. д., приводят к отклонению движения от опорной (невозмущенной. программной) траектории, а суммарное возмущение движения описывается вектором – функциями

∆у(t); + ∆ и (t)

и в соответствии с (4,1) векторным уравнением

(4.2)

Опорная траектория описывается уравнением

(Н.У.) (4.3) Раскладывая правую часть (4.2) в ряд Тейлора относительно опорных значений: 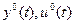, ограничиваясь линейными членами и вычитая (4.3) из (4.2) получаем

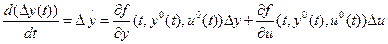(4.4)

Здесь был использован «метод малых возмущений», в соответствии с которым составляющие более высокого порядка по сравнению с линейными становятся пренебрежительно малыми.

Систему линейных дифференциальных уравнений(4.4) можно разделить на две подсистемы, которые обычно исследуются независимо. Например, если за опорное движение принять прямолинейный полёт без крена и скольжения, то производные компонентов полного вектора сил 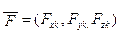и полного вектора момента в силу симметрии ВС относительно плоскости OXY равны

;

.

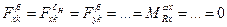При этом в первой системе параметрами являются: 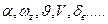- для описания продольного движения. Во второй: - для описания бокового возмущённого движения. Система уравнений, описывающих продольное возмущенное движение в результате «разделения» имеет вид

1. ;

2. ;

3. ;

4. ; (4.5)

5. ;

6. ;

7. .

Система управления бокового возмущенного движения

1. ;

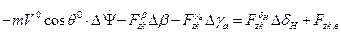2. ;

3. ;

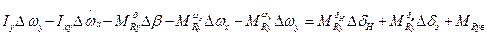4. ;

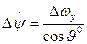5. ; (4.6)

6. ;

7. ;

8. .

В уравнениях (4.5), (4.6) величины 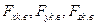; - представляют собой возмущающие силы и моменты (воздействие ветра, упругих колебаний конструкции и т.п.)

4.1. Математические методы исследования.

Системы уравнений (4.4), (4.5) и (4.6) являются неоднородными линейными дифференциальными уравнениями в общем случае с переменными коэффициентами. В случае, если в правую часть явно не входит независимая переменная «t» и производные в правой части этих уравнений изменяются незначительно, то их принимают постоянными на маленьком отрезке времени (в соответствии с «методом замороженных коэффициентов» и системы уравнений ставятся системами дифференциальных уравнений с постоянными коэффициентами. При ∆ 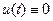в уравнении (4.4) система ставится однородной и описывает собственные возмущения движения ВС (при ∆ 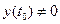). Такое движение можно получить, если находящемуся в равновесном режиме полёта ВС сообщить некоторые начальные возмущения, а затем предоставить самому себе.

4.1.1. Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методОМ. Теоремы А.М. Ляпунова об устойчивости

При исследовании собственного возмущения движения ВС выясняется устойчивость опорного движения. Анализ вынужденного движения позволяет определить реакцию ВС на управляющие воздействия и сделать оценку его управляемости. Рассмотрим решение однородной системы дифференциальных уравнений (4.4) (с целью дальнего исследования устойчивости) при ∆ .

(4.7)

Пусть по методу замороженных коэффициентов 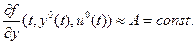и система (4.7) приводится к виду

(Н.У.) (4.8)

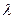Решение будем искать в виде ,где С– некоторой постоянный вектор – столбец, координаты которого зависят от выбора Н.У: ; - постоянное число. Подставим решение в исходное уравнение ,

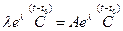откуда

(4.9)

Так как все элементы С не могут быть равны нулю, то для того чтобы существовало нетривиальное решение системы (4.9) относительно вектора С, необходимо и достаточно, чтобы

(4.10)

Это соотношение представляет алгебраическое уравнение n-ой степени относительно 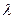и называется характеристическим уравнением (многочленом). Его корни являются собственными числами матрицы А. Для каждого можно получить решение 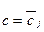системы (4.9). Итак, частным решением системы (4.8) будет

(4.11)

а общее, как линейная комбинация частных решений

(4.12)

Эта линейная комбинация является общим решением системы только, если все действительны и различны. Подставляя в (4.12) Н.У., получаем при

(4.13)

Это уравнение относительно неизвестных является неоднородным и решение можно найти по формуле Крамера.

Из построенного общего решения (4.12) видно, что когда все действительны, то отклонения от невозмущенной (опорной) траектории изменяются по апериодическому (экспоненциальному) закону и будет возрастать или убывать в зависимости от знаков корней . Если все корни будут отрицательными, то при 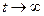компоненты 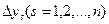вектора стремятся к нулю и, следовательно, невозмущенное движение будет асимптотически устойчивым. Если хотя бы один из корней будет положительным, то из (4.12) видно, что компоненты будут возрастать с течением времени при сколь угодно малых начальных отклонениях и таким образом невозмущенное (опорное) движение будет неустойчивым.

Дата добавления: 2015-08-27