Динамика продольного возмущенного движения ВС 2 страница

Характеристическое уравнение системы (5.18)

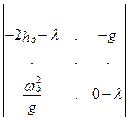= λ² + 2 h_д λ + ω_д² = 0. (5.21)

Условиями асимптотической устойчивости опорного движения (горизонтального полета с постоянной скоростью) является: 2h_д>0 и ω_д²>0. Первое условие (см. (5.20)) зависит от знака величин 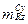= (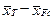); ( 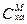- 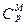) и 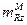. При этом 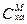, 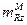определяются при постоянном значении α_бал горизонтального полета, а C_p^M – для постоянного режима работы двигателя (положения рычага управления двигателем (РУД)). Второе условие ω_д²>0 при 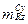<0 выполняется при σ_V<0. Корни уравнения (5.21): λ_1,2 = -h_д ± .

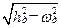Если ω_д²> h_д² и ω_д²>0, то корни будут комплексными сопряженными λ_1,2 = -h_д ± i 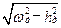, а собственное длиннопериодическое движение называют колебательным или фугоидным и решения (5.18) равны

;

,

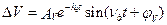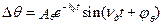где h_д – коэффициент демпфирования; 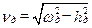-круговая частота собственных колебаний; ω_д – опорная частота или частота недемпфированных колебаний; φ_V, φ_θ – фазовые углы сдвига.

При 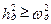корни характеристического уравнения будут действительными, а собственное движение – апериодическим. Решение при этом будет

;

,

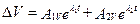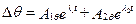а при , ; ; .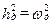

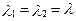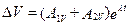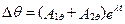Постоянные A_V, A_θ, A_1V, A_2V, A_1θ, A_2θ – определяются из начальных условий при t = t₀.

Если σ_V>0, ω_д²<0 один из корней λ₁ или λ₂ положительный и опорное движение апериодически неустойчивое. Если h_д<0, a ω_д²>0 возможны два вида неустойчивости: при h_д²>ω_д² – будут два действительных положительных корня и неустойчивость будет апериодической, а при ω_д²>h_д² – колебательная (фугоидная) неустойчивость.

5.3 Реакция ВС в продольном движении на отклонение органов управления

При изучении переходных процессов удобно пользоваться передаточными функциями, которые чаще всего рассматривают раздельно для короткопериодического и длиннопериодического возмущенных движений.

5.3.1 Передаточные функции ВС в короткопериодическом возмущенном движении

Уравнения движения от рассмотренных ранее в разделе 5.2.1 отличаются наличием управляющих воздействий (см.(5.1), (5.2), (4.5))

;

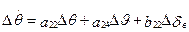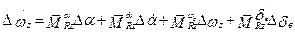; (5.22)

,

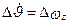где Δ 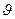=Δθ + Δα, Δθ = Δ 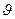– Δα, .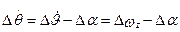

(Иногда обозначается ω_z вместо Δω_z, т.к. в опорном режиме полета 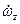= 0);

; ; ; .

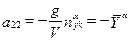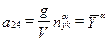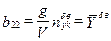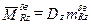Представим систему уравнений (5.22) в операторной форме с помощью таблицы 2 (раздел 4.1.2) при нулевых начальных условиях (индекс «Δ» опускаем)

;

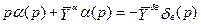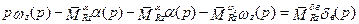; (5.23)

.

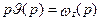Решая эту систему уравнений, найдем передаточные функции (с точностью до )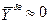

;

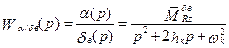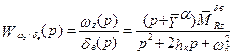(5.24)

.

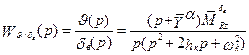Обычно передаточные функции приводят к каноническому виду, в которых параметры канонической формы должны быть положительными. Передаточные коэффициенты

; ; ;

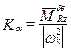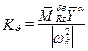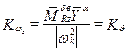постоянные времени: ; ;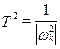

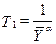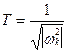
Относительный коэффициент демпфирования ;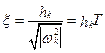

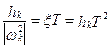
В канонической форме

;

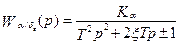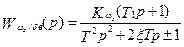; (5.25)

.

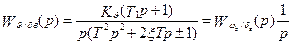Знаки (±) свободного члена в знаменателе принимаются соответственно для ВС с про-

дольной статической устойчивостью по перегрузке (+) и неустойчивостью по перегрузке (-).

Аналогично вводятся передаточные функции 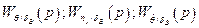и другие.

Приведем здесь перечень некоторых из решаемых задач динамики полета с помощью передаточных функций.

I. Используя знаменатель передаточной функции можно исследовать динамическую устойчивость (по Ляпунову) по первому приближению, т.к. знаменатель по форме совпадает с характеристическим уравнением с той лишь разницей, что вместо «λ» стоит параметр «p». (сравним (5.13) и первое уравнение (5.24)).

II. Если в качестве входного воздействия принять 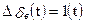в (5.24), то изображение по Лапласу 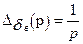и W_α/δв(p) = p α(p) можно использовать для определения установившегося значения переходной функции y(t) на основе теоремы

2) (4.21) (в общем случае X(p) = 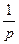, W_yx(p) = 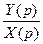= p Y(p)).

.

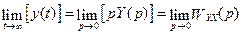III. При построении систем автоматического управления (САУ) изучаются

передаточные функции «замкнутых» систем, являющихся функциями исходных W(p) и проблема сводится к выбору параметров САУ такими, чтобы характеристики устойчивости и управляемости ВС были оптимальными, удовлетворяющими нормативным документам (АП – 25 и др.).

IV. Для устойчивых систем от W(p) нетрудно перейти к частотным характеристикам, положив p = iω и исследовать показатели («запасы») устойчивости и управляемости по АФЧХ.

V. Некоторые из показателей статической управляемости можно вычислить непосредственно по W_YX(p).

VI. С помощью перехода от изображений к оригиналам можно проводить исследования во временной области.

В заключении заметим, что обычно для ВС составляются перечни (таблицы, «библиотека») передаточных функций, которые широко используются при решении различных задач динамики полета.

Лекция 9. 5.3.2 Характеристики переходных процессов в короткопериодическом движении

Поведение ВС в короткопериодическом (быстром, вращательном) движении определяется потребной нормальной скоростной перегрузкой n_ya для угловой ориентации, точной стабилизации. Определим сначала передаточную функцию 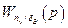. Перегрузка

;

(; ; ),

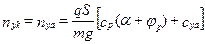
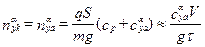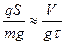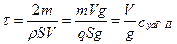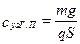или, в возмущенном движении,

;

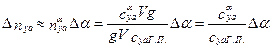и преобразование Лапласа

Δn_ya(p) = 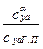Δα(p).

Передаточная функция 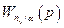= 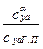и поскольку величина n_yk^α = n_ya^α = 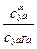, то можно воспользоваться обозначением, принятым в системе уравнений (5.22) n_ya^α = 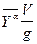, тогда = .

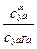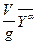Передаточная функция 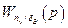может быть представлена следующим образом

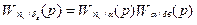
и с учетом предыдущих соотношений и (5.25)

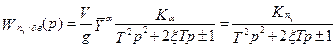(5.26)

(перед единицей в знаменателе принимается «+» для устойчивых систем), где 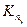= 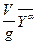K_α и K_α с использованием (5.12)

.

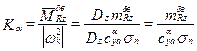Определим теперь коэффициент K_ny

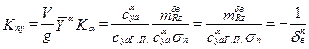, (5.27)

поскольку из условия балансировки 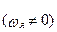и уравнения (2.47) было выведено ранее

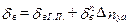и .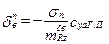

Рассмотрим решение одной из задач, когда в качестве входного воздействия принято δ_в(t) = 1(t) и соответственно δ_в(p) = 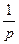. Определим переходную функцию, описывающую переходный процесс по времени при ступенчатом отклонении рулей в возмущенном движении. Переходя от изображения Δn_ya(p) = W_ny/δв Δδ_в(p) к оригиналу, получим ().

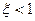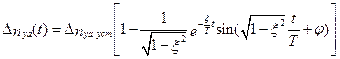(5.28)

или

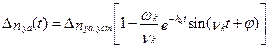, (5.29)

где Δn_yaуст проще вычислить, как предел на основе теоремы 2 (формула 4.21).

.

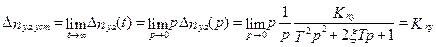Здесь Т – постоянная времени; 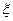- относительный коэффициент демпфирования;

φ = arcsin 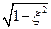- сдвиг собственных колебаний по фазе; 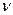_к = .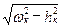

На основании (5.28), (5.29) можно определить динамические показатели устойчивости и управляемости ВС, по которым оценивают качество переходного процесса

период собственных колебаний ВС

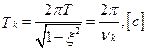(5.30)

частоту собственных колебаний

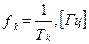(5.31)

время переходного процесса, например, когда Δn_ya(t) входит в 5% трубку «относительно установившегося состояния» Δn_yaуст, т.е. по (5.29).

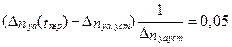или ,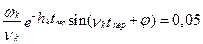

откуда приближенно

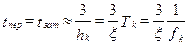(5.32)

(t_пер – иногда называют временем затухания).

Число колебаний до практически полного затухания

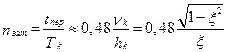. (5.33)

Относительный заброс перегрузки при достижении своего первого экспериментального значения

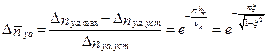(5.34)

соответствует моменту времени t₁ = ;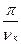

время срабатывания – время первого выхода регулируемого параметра движения на его установившееся значение (в частности, Δn_yaуст) или, при 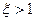, на значение равное 0,95 от установившегося значения в случае апериодического переходного процесса

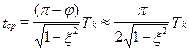(5.35)

Иногда рассматривают изменение амплитуды колебаний за один период, время уменьшения амплитуды вдвое (t₂) и т.п….

Основные характеристики колебательного переходного процесса (переходной функции) представлены на рис.33.

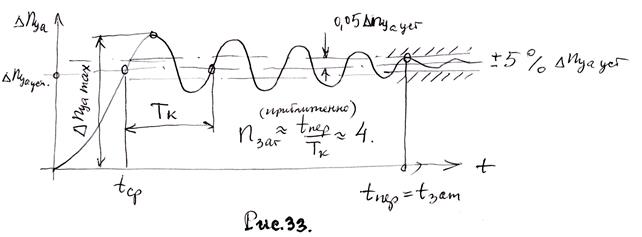Относительный заброс перегрузки (иногда называют величиной перерегулирования), как видно из (5.34) зависит от 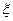. Аналогично от 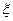зависит t_пер = t_зат. Приближенные зависимости представлены на рис.34.

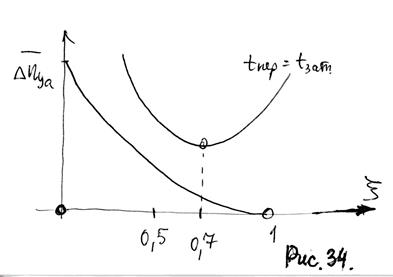
Из рисунка видно, что при 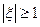( 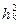> 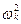) переходный процесс становится апериодическим и корни уравнения p² + 2h_k p + 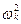= 0 действительные. Тогда (p_i )

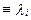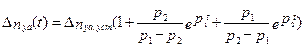. (5.36)

5.3.3 Передаточные функции возмущенного траекторного движения ВС в вертикальной плоскости (включая длиннопериодическое). Уравнения возмущенного движения ВС с учетом (5.2) и (5.17) рассматриваются для 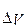, , 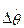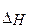и 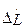. В этих уравнениях производится учет влияния ΔH на ΔV и Δθ, и в качестве управляющих воздействий вместо Δc_p и Δδ_в приня- ты Δn_дв = 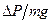и Δ 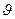. В традиционных уравнениях 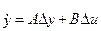коэффициенты 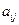следу- ющие: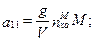

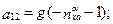
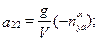
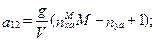
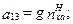
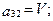
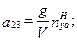
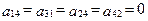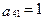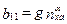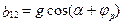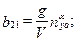
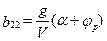; ; ; ; . После преобразования Лапласа при нулевых начальных условиях нетрудно получить передаточные функции траекторного движения ЦМ ВС в канале тангажа:

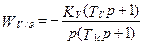; (5.37)

где: ; ; ;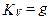

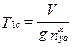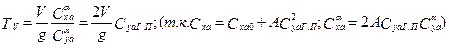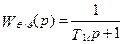; (5.38)

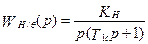, (5.39)

где ;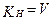

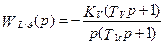. (5.40)

Передаточные функции в канале двигателя

(5.41)

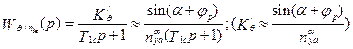(5.42)

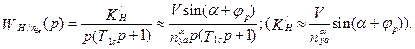(5.43)

В траекторном движении принимается, что ВС сбалансировано и приближенно

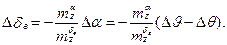Кроме того,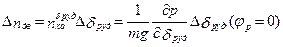

5.3.4 Схемы основных передаточных функций. Канал руля высоты (δ_в; φ)

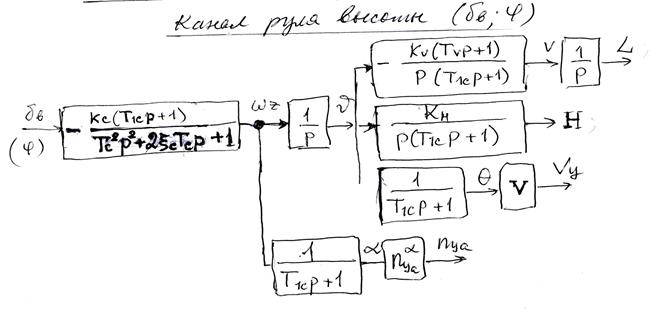
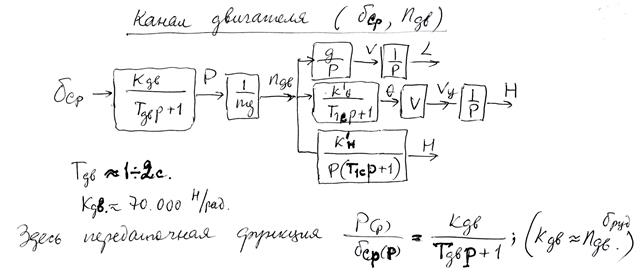приближенно описывает динамику запаздывания установления тяги двигателя. Возможны и другие более точные математические модели, описывающие работу двигателя.

6. Динамика бокового возмущенного движения ВС

Будем полагать, что управление продольным движением определено и фиксировано, а начальное отклонение параметров продольного движения и возмущающие действия, влияющие на продольное движение, отсутствуют. Ввиду того, что боковое движение сопровождается вращением относительно двух осей OX и OY, оно в известном смысле сложнее, чем продольное относительно оси OZ. При достаточно больших возмущениях боковое движение вызывает существенное изменение параметров продольного и изолированное боковое возмущенное движение изучать некорректно. Таким образом, в отличие от продольного изолированное боковое движение может рассматриваться только при малых возмущениях. В боковом движении действуют гироскопические, инерционные моменты, а также силы и моменты, обусловленные аэродинамическим и кинематическим воздействием. Чтобы упростить исследования бокового возмущенного движения примем за опорный (невозмущенный) -прямолинейный установившийся (V ْ = const), горизонтальный (H ْ =const, α ْ =α_бал =const, θ ْ = 0, α_бал ْ = 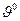) полет без крена и скольжения (γ_а ْ =β ْ =0).

6.1 Уравнения бокового возмущенного движения

Уравнения бокового возмущенного движения относительно произвольного опорного (невозмущенного) режима движения рассмотрены ранее и представлены в виде системы (4.6). Если в качестве опорного принять режим, указанный выше, то система уравнений упрощается и с учетом малости углов γ, β(γ, β≤20 ْ ) и кинетических соотношений, получим

;

;

;

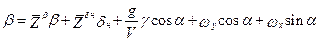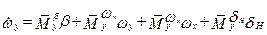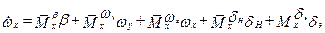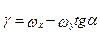; (6.1)

;

.

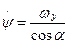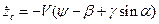Здесь приняты допущения и обозначения: ; ; ;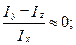

; ; ; ; ; ;

; ; ; ; ; ;

; ; ; ; ; ;

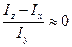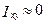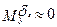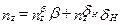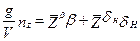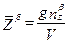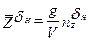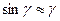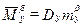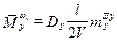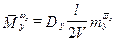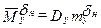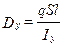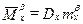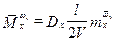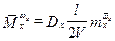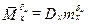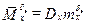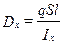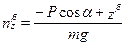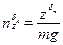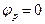, т.к. 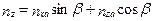, , 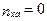то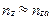

.

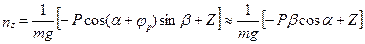Вводя стандартные матричные обозначения для системы (6.1), имеем

.

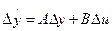После преобразования Лапласа при нулевых начальных условиях 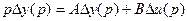, которое приводится к виду

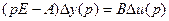. (6.2)

6.2 Устойчивость в боковом возмущенном движении.

В уравнении (6.2) (pE - A), совпадающее по форме с (λE - A) и может быть использовано для составления характеристического уравнения

,

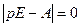после раскрытия которого, получаем

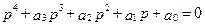, (6.3)

где: ;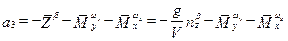

;

.

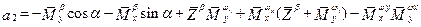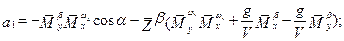
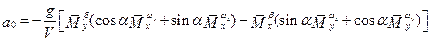Уравнение (6.3) приводится к виду

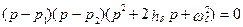(6.4)

Здесь 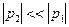. Приближенное значение большого корня 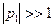можно получить, пренебрегая в уравнении (6.3) слагаемыми со степенями p ниже третьей. Получим 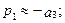или

Дата добавления: 2015-08-27