
|
Читайте также: |
Рассмотрим случай, когда среди корней характеристического уравнения имеются комплексные сопряженные. Пусть два корня:  . Этим корням соответствует частное решение
. Этим корням соответствует частное решение

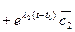 ,
,
где  и
и  определяются из системы (4.9) и являются комплексными сопряженными векторами
определяются из системы (4.9) и являются комплексными сопряженными векторами  =
=  -i
-i 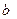 ;
;  =
=  +i
+i 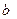 ;
;
Компонент, соответствующий «S»-строке может быть представлен в виде

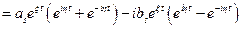
(здесь для простоты дальнейших преобразований принято 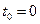 ). Пользуясь формулой Эйлера
). Пользуясь формулой Эйлера  ;
;  , получим
, получим 

 , где
, где 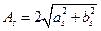 ,
,  - новые производные постоянные. Откуда видно, что частое движение, соответствующее паре комплексных сопряжённых корней, будет колебательным с амплитудой
- новые производные постоянные. Откуда видно, что частое движение, соответствующее паре комплексных сопряжённых корней, будет колебательным с амплитудой  , круговой частотой
, круговой частотой  и фазой
и фазой  . Амплитуда будет неограниченно возрастать, если вещественная часть комплексного корня – положительная
. Амплитуда будет неограниченно возрастать, если вещественная часть комплексного корня – положительная  и затухать если
и затухать если  . Поскольку общее решение будет содержать колебательную составляющую, то для устойчивости невозмущенного движения вещественные части корней должны быть отрицательными. Это, является основным содержанием теоремы А.М. Ляпунова об устойчивости по первому приближению.
. Поскольку общее решение будет содержать колебательную составляющую, то для устойчивости невозмущенного движения вещественные части корней должны быть отрицательными. Это, является основным содержанием теоремы А.М. Ляпунова об устойчивости по первому приближению.
Пусть исходная динамическая система описывается векторным уравнением
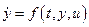 , (4.14)
, (4.14)
где  мерный вектор,
мерный вектор,  мерный вектор,
мерный вектор,  мерная непрерывная вещественная вектор-функция, заданная в ограниченной области переменных «у» и«n» и удовлетворяющая условиям Липшица.
мерная непрерывная вещественная вектор-функция, заданная в ограниченной области переменных «у» и«n» и удовлетворяющая условиям Липшица.
Пусть для  - начального условия в моменты времени
- начального условия в моменты времени  и заданного управления
и заданного управления 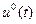 получено единственное решение (4.14), которое называется невозмущенным (опорным, программным) движением.
получено единственное решение (4.14), которое называется невозмущенным (опорным, программным) движением.

Решение той же системы (4.14) с заданным управлением  , но с другим начальным условием
, но с другим начальным условием  называется возмущенным и исследование устойчивости движения сводится к исследованию свойств решений возмущенного движения
называется возмущенным и исследование устойчивости движения сводится к исследованию свойств решений возмущенного движения  .Для анализа возмущенного движения сделаем замену переменных:
.Для анализа возмущенного движения сделаем замену переменных:

и поскольку невозмущенное движение удовлетворяет исходному уравнению(4.14)

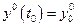 (Н.У.)
(Н.У.)
то для возмущенного движения с учетом замены переменных, получаем
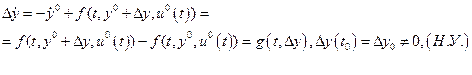
Очевидно, что исследование на устойчивость 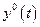 исходной системы может быть заменено исследованием на устойчивость преобразованной системы или, что одно и то же, расположенной в начале координат точки покоя
исходной системы может быть заменено исследованием на устойчивость преобразованной системы или, что одно и то же, расположенной в начале координат точки покоя  . При исследовании точки покоя
. При исследовании точки покоя  нелинейной системы представим ее в виде:
нелинейной системы представим ее в виде:
 , (4.15)
, (4.15)
где R(t, Δy) – имеет порядок выше первого относительно 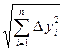 . Вместо точки покоя нелинейной преобразованной системы (4.15) будем исследовать устойчивость точки покоя Δy
. Вместо точки покоя нелинейной преобразованной системы (4.15) будем исследовать устойчивость точки покоя Δy 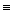 0 линейной системы:
0 линейной системы:
 =A(t) Δy, (4.16)
=A(t) Δy, (4.16)
называемой системой уравнений первого приближения для нелинейной (4.15).
Исследование на устойчивость линеаризованной системы остается проблематичным в случае переменной матрицы A(t) и значительно упрощается, если элементы матрицы А постоянны (A=const), т.е. исходная система и, следовательно, считать, что преобразованная стационарна в первом приближении. А.М. Ляпунов доказал основные теоремы.
Теорема об устойчивости
Если система (4.15) стационарна в первом приближении, все члены Ri в достаточномалойокрестности начала координат при t≥T≥t0 удовлетворяют неравенствам  ,
,
где N и α - постоянные, причем α>0 (т.е. если Ri не зависит от t, то их порядок выше первого относительно  ) и все корни характеристического уравнения
) и все корни характеристического уравнения
|A - λ E|=0
имеют отрицательные действительные части, то тривиальное решение y 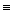 0 системы уравнений (4.15) и решение системы уравнений (4.16) асимметрически устойчиво, следовательно, в этом случае возможно исследование на устойчивость по первому приближению.
0 системы уравнений (4.15) и решение системы уравнений (4.16) асимметрически устойчиво, следовательно, в этом случае возможно исследование на устойчивость по первому приближению.
Теорема о неустойчивости
Если в условиях первой теоремы хотя бы один корень характеристического
уравнения имеет положительную действительную часть, то точки покоя Δy 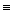 0 системы (4.15) и (4.16) неустойчивы, следовательно, и в этом случае возможно исследование на устойчивость по первому приближению.
0 системы (4.15) и (4.16) неустойчивы, следовательно, и в этом случае возможно исследование на устойчивость по первому приближению.
Эти теоремы не охватывают случай, когда корни характеристического уравнения чисто мнимые (или когда вещественная часть хотя бы одного корня равна нулю). В таком критическом случае начинают влиять на устойчивость нелинейные члены Ri и исследование на устойчивость по первому приближению, вообще говоря, невозможно.
Непосредственное исследование устойчивости невозмущенного движения (или точки покоя Δy 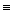 0 преобразованной системы) является простым лишь для уравнений первого и второго порядков. Поэтому для решения вопроса об устойчивости или неустойчивости разработаны косвенные признаки, по которым можно судить о знаке вещественной части корней характеристического уравнения, минуя вычисление самих корней, которые называются критериями устойчивости.
0 преобразованной системы) является простым лишь для уравнений первого и второго порядков. Поэтому для решения вопроса об устойчивости или неустойчивости разработаны косвенные признаки, по которым можно судить о знаке вещественной части корней характеристического уравнения, минуя вычисление самих корней, которые называются критериями устойчивости.
По критериям устойчивости можно судить об устойчивости линейной стандартной системы, определять границы устойчивости и выбирать параметры устойчивой системы.
Критерии устойчивости подразделяются на алгебраические и частные. Алгебраические критерии позволяют судить об устойчивости и неустойчивости систем по коэффициентам характеристического уравнения. Имеются различные формы критериев. Наибольшее применение получили критерии Гурвица и Рауса.
Приведем без доказательства теорему Гурвица.
Пусть характеристическое уравнение n-ой степени имеет вид
anλn+an-1λn-1+…+a1λ+a0=0 (4.17)
в котором все коэффициенты ak – вещественные числа, а an>0. Построим из коэффициентов ak матрицу Гурвица (nxn):


Теорема Гурвица
Для того чтобы все корни характеристического уравнения (4.17) имели отрицательные вещественные части, необходимо и достаточно, чтобы все главные диагональные миноры матрицы Гурвица были положительны:
Δ1 = an-1>0;  ; …; Δn = a0 Δn-1>0. (4.18)
; …; Δn = a0 Δn-1>0. (4.18)
Пример: Дано уравнение четвертой степени
λ4+a3λ3+a2λ2+a1λ+a0=0 (a4=1) (4.19)
Для «устойчивого движения» должны выполняться условия
Δ 1 = a3>0;  ;
;  ; Δ 4 = a0 Δ 3 > 0.
; Δ 4 = a0 Δ 3 > 0.
Равносильными для уравнения 4-ой степени являются условия Рауса-Гурвица:
a0>0; a1>0; a2>0; a3>0; R=Δ3=a1 a2 a3 - a12-a0 a32>0. (4.20)
Найдем границы устойчивости
На границе устойчивости будут равны нулю действительный корень (λ=0) или вещественная часть комплексных сопряженных корней:  ; (
; (  ). Если подставить в (4.17) значение λ = 0, то получим границу апериодической устойчивости, а0=0 или Δ n = 0 (при всех остальных положительных минорах матрицы Гурвица). Подставляя в уравнение (4.17) вместо
). Если подставить в (4.17) значение λ = 0, то получим границу апериодической устойчивости, а0=0 или Δ n = 0 (при всех остальных положительных минорах матрицы Гурвица). Подставляя в уравнение (4.17) вместо  его значения:
его значения: 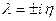 , получим границу колебательной устойчивости:
, получим границу колебательной устойчивости:  , причем все остальные миноры матрицы Гурвица положительны. Третья граница устойчивости соответствует бесконечному корню
, причем все остальные миноры матрицы Гурвица положительны. Третья граница устойчивости соответствует бесконечному корню 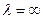 и согласно уравнению (4.17) будет при аn = 0 (что на практике встретить затруднительно).
и согласно уравнению (4.17) будет при аn = 0 (что на практике встретить затруднительно).
4.1.2. Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом
В теории автоматического управления полетом, при исследовании и решении задач управляемости широко используется операторный метод решения дифференциальных уравнений.
В качестве интегрального преобразования обычно используют преобразование Лапласа
 ,
,
где параметр p – некоторое комплексное число; y(t) – кусочно-непрерывная и ограниченная функция независимой переменной t, называемая оригиналом; Y(p) – изображение функции y(t). Помимо прямого преобразования, существует обратное преобразование, позволяющее по изображению Y(p) находить оригинал y(t). Сокращенное обозначение обратного преобразования  = y(t).
= y(t).
Таблица
| Математическая операция | Оригинал | Изображение |
| Исходное преобразование | y(t) | Y(p) |
| Сложение оригинала | y1(t)+y2(t) | Y1(p)+Y2(p) |
| Умножение на постоянное число | a y(t) | a Y(p) |
| Дифференцирование | dy/dx | p Y(p) – y0 |
| n-кратное дифференцирование | dny/dtn | 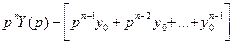
|
| Интегрирование | 
| 
|
| Сдвиг оригинала на τ | y(t-τ) | 
|
В таблице y0,  ,…,
,…, 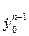 обозначены Н.У. при t=0 (обычно).
обозначены Н.У. при t=0 (обычно).
При анализе возмущенного движения ВС иногда возникает необходимость определить предельные значения решения дифференциального уравнения по виду этого уравнения, не интегрируя его. Эту задачу можно решить с помощью следующих теорем о предельном переходе:
1. Если существует предел функции 
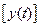 , то
, то

 =
=  . (4.20)
. (4.20)
2. Если существует предел функции  , то
, то
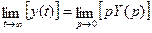 . (4.21)
. (4.21)
Лекция 8. 4.1.3. Исследование управляемого движения с помощью передаточных функций
При выполнении летной операции управляющие воздействия формируются в соответствии с заданной программой полета. Результат управления зависит от реакции ВС на управляющие воздействия. Обычно для оценки управляемости различных ВС принято рассматривать их реакцию на скачкообразное (ступенчатое) или гармоническое отклонение органов управления. При ступенчатом отклонении изучаются переходные или временные характеристики (функции) ВС, а при гармоническом – частотные характеристики (функции). Частотными характеристиками системы (звена), называют зависимость отношения амплитуд выходной величины к входной и сдвига по фазе выходной величины по отношению к входной от частоты входного воздействия.
Передаточной функцией называют отношение изображений выходной величины к входной при нулевых начальных условиях:
 . (4.22)
. (4.22)
Здесь Y(p) u X(p) - соответственно изображение по Лапласу выходной и входной величины.
Для изучения реакции ВС в частотной области на вход подается гармоническое воздействие (сигнал) Δu(t)=A1 sin( t) для следующей системы уравнений
t) для следующей системы уравнений
 . (4.23)
. (4.23)
Здесь предполагается, что имеется отклонение от программного управления 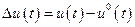 и решение (4.23) состоит из «собственной» и «вынужденной» составляющих решений. Собственная составляющая, зависящая от начальных условий Δy(t0), как решение уравнения
и решение (4.23) состоит из «собственной» и «вынужденной» составляющих решений. Собственная составляющая, зависящая от начальных условий Δy(t0), как решение уравнения 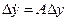 для устойчивых систем затухает с течением времени. Вынужденная составляющая, определяемая как частное решение (4.23), будет в силу линейности системы, также гармонической
для устойчивых систем затухает с течением времени. Вынужденная составляющая, определяемая как частное решение (4.23), будет в силу линейности системы, также гармонической
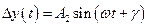 (4.24)
(4.24)
где A2 и  – амплитуда и частота вынужденных колебаний выходной величины; γ - сдвиг по фазе.
– амплитуда и частота вынужденных колебаний выходной величины; γ - сдвиг по фазе.
При изучении выходных характеристик y(t),будем пренебрегать «собственной» составляющей решений и ограничиваться только «вынужденной» составляющей.
В этом случае A2 и γ можно определить по частотной функции W(i  ). Можно показать (см. Приложение 2), что W(i
). Можно показать (см. Приложение 2), что W(i  ). что получается из передаточной W(p)=
). что получается из передаточной W(p)=  (где Y(p)
(где Y(p) 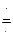 Δy(t), U(p)
Δy(t), U(p) 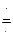 Δu(t)) путем замены p=i
Δu(t)) путем замены p=i  , где
, где  – частота вынужденных колебаний. Частотную функцию (как комплексное число) представим в виде:
– частота вынужденных колебаний. Частотную функцию (как комплексное число) представим в виде:
W(i  )=Re(
)=Re( )+
)+ 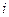 Im(
Im( )=A(
)=A( )ei γ (ω) , (4.25)
)ei γ (ω) , (4.25)
где Re( ), Im(
), Im( ) – соответственно действительная и мнимая часть частотной функции;
) – соответственно действительная и мнимая часть частотной функции;  - модуль частотной функции, называется амплитудно-частотной характеристикой (АЧХ); γ(ω)=arg W(iω) – аргумент частотной функции, называется фазовой частотной характеристикой (ФЧХ). Модуль и аргумент частотной функции изображены на рис. 32.
- модуль частотной функции, называется амплитудно-частотной характеристикой (АЧХ); γ(ω)=arg W(iω) – аргумент частотной функции, называется фазовой частотной характеристикой (ФЧХ). Модуль и аргумент частотной функции изображены на рис. 32.

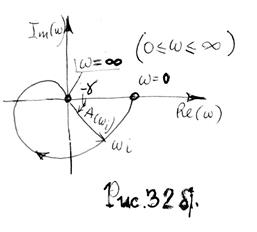
При этом:  ;
;  .
.
С помощью этих выражений можно построить (рис.32.б) амплитудно-фазовую частотную характеристику (АФЧХ), при изменении ω от о до ∞ (строить зависимость при -∞<ω<+∞ нет необходимости, т.к. кривые симметричные относительно оси абсцисс).
АФЧХ также как передаточная функция W(p) и дифференциальное уравнение системы определяет ее динамические свойства, но обладает тем преимуществом, что может быть построена экспериментально.
Дата добавления: 2015-08-27; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аннотация. 5 страница | | | Динамика продольного возмущенного движения ВС 1 страница |