
|
Читайте также: |
В разделе 4 получены формулы (4,5), описывающие продольное возмущенное движение. Принимается β=γa=0, m(t)=const, изменение аэродинамических сил по высоте мало,
 ,
,  ,
,  ;
;
пренебрегается изменением по высоте ρ(H), p(H), a(H), полагая момент тангажа сбалансированным в опорном движении  . Для упрощений уравнений возмущенного движения целесообразно перейти от производных сил к производным перегрузок, учитывая что
. Для упрощений уравнений возмущенного движения целесообразно перейти от производных сил к производным перегрузок, учитывая что
nya=  (P sin(α+φp)+Ya); nxa=
(P sin(α+φp)+Ya); nxa=  (P cos(α+φp)-Xa);
(P cos(α+φp)-Xa);
при (γa=0, β=0): nya=nyk; nxa=nxk; M=  ;
;  .
.
Проделаем преобразования на примере первого уравнения  и уравнения для описания опорного движения
и уравнения для описания опорного движения 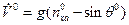 . Уравнение в отклонениях от опорного (возмущенного) запишем в виде (принимая во внимание:
. Уравнение в отклонениях от опорного (возмущенного) запишем в виде (принимая во внимание:  )
)

Проделав аналогичные преобразования можно уравнения (4.5) представить в матричной форме.
 , (5.1)
, (5.1)
где
 ;
;  ;
;  ;
;  ;
;  ; (5.2)
; (5.2)
a11 = g nxkV =  nxkM M; a21 =
nxkM M; a21 =  (nykM M – nyk + cos θ); a12 = g(nxkθ – cos θ)=g(-nxkα – cos θ);
(nykM M – nyk + cos θ); a12 = g(nxkθ – cos θ)=g(-nxkα – cos θ);
a22 =  (nykθ + sin θ) =
(nykθ + sin θ) =  (-nykα + sin θ); a14 =
(-nykα + sin θ); a14 =  = g nxkα; a24 =
= g nxkα; a24 = 
 =
=  nykα;
nykα;
Dz =  ; a31 =
; a31 =  (2mz + 2mpz1 + mzM M + mpz1MM); a32 = Dz mzθ; a33 = Dz mzωz;
(2mz + 2mpz1 + mzM M + mpz1MM); a32 = Dz mzθ; a33 = Dz mzωz;
a34 = Dz  ; a51 = sin θ; a52 = V cos θ; a61 = cos θ; a62 = -V sin θ; b11 = g
; a51 = sin θ; a52 = V cos θ; a61 = cos θ; a62 = -V sin θ; b11 = g  ;
;
b21 = 
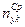 ; b31 = Dz
; b31 = Dz  ; b22 =
; b22 =  nykδв; b32 = Dz mzδв.
nykδв; b32 = Dz mzδв.
В системе (5.1) параметры ΔH и ΔL не входят в правые части четырех первых уравнений и нe влияют на изменение соответствующих фазовых переменных, поэтому могут рассматриваться независимо от двух последних.
5.1. Собственное продольное возмущенное движение ВС. Условия устойчивости опорного движения
В опорном режиме полета управление  u˚(t) = (P˚(t), δb˚(t)) задано и изменение
u˚(t) = (P˚(t), δb˚(t)) задано и изменение  Рассмотрим уравнения продольного собственного возмущенного движения (см. (5.1), без включения строк и столбцов, соответствующих ΔH и ΔL).
Рассмотрим уравнения продольного собственного возмущенного движения (см. (5.1), без включения строк и столбцов, соответствующих ΔH и ΔL).
 (5.3)
(5.3)
Характеристический многочлен
|A - λE| = |λE - A| = 0, (5.4)
или
 .
.
Раскрывая определитель по последней строке, получаем:
λ4 + a3 λ3 + a2 λ2 + a1 λ + a0 = 0, (5.5)
где: a3 = -a11 – a22 – a33; a2 = a11 a22 + a22 a33 + a11 a33 – a21 a12 + a34;
a1 = - a11 a34 – a22 a34 + a31 a14 + a32 a24;
a0 = a11 a22 a34 + a21 a32 a14 + a31 a12 a24 – a31 a14 a22 – a21 a12 a34 – a11 a32 a24.
Для асимптотической устойчивости в соответствии с условиями Рауса – Гурвица должно соблюдаться:
a0>0; a1>0; a2>0; a3>0; R = a1 a2 a3 – a12 – a0 a32>0.
Возмущенное движение в целом по всему вектору Δy = (ΔV, Δθ, Δωz, Δ 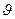 , ΔH, ΔL) можно проанализировать по уравнениям для ΔH и ΔL, т.е. пусть
, ΔH, ΔL) можно проанализировать по уравнениям для ΔH и ΔL, т.е. пусть  = V Δθ;
= V Δθ;  = ΔV. Интегрированием этих уравнений получаем:
= ΔV. Интегрированием этих уравнений получаем:
ΔH(t) = V  ; (ΔH0≠0)
; (ΔH0≠0)
ΔL(t) = 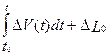 ; (ΔL0≠0)
; (ΔL0≠0)
Откуда видно, что если ВС асимптотически устойчиво по Δθ(t) и ΔV(t), т.е. при t→∞ Δθ(t)→0, ΔV(t)→0, то при этих условиях ΔH(t)→ΔH0 и ΔL(t)→ΔL0 и движение не будет асимтотически устойчивым, но может быть просто устойчивым по Ляпунову при малых ΔH0 и ΔL0.
5.2 Выделение быстрой и медленной составляющих продольного возмущенного движения
Исследования решений уравнения (5.5) показывают, что для большинства ВС имеются два больших λ12 = ξ1±iη1 и два маленьких λ12 = ξ1±iη2. Причем одна пара корней |λ1,2|>>|λ3,4| и отличается в десятки раз. Движение с большими |λ1,2| будет быстро затухающим (чаще всего колебательным) и называется короткопериодическим, а с малыми |λ3,4 | - длиннопериодическим или медленным. Быстро изменяются: Δα(t), Δωz(t), Δ 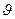 (t). Медленно изменяются: ΔV(t), Δθ(t). При исследовании быстроизменяющихся параметров можно принять ΔV≈0, т.е. изменение скорости не успевает произойти V = V˚ = const, а при изучении ΔV(t), Δθ(t) можно считать, что быстрое изменение Δα(t), Δωz(t) и Δ
(t). Медленно изменяются: ΔV(t), Δθ(t). При исследовании быстроизменяющихся параметров можно принять ΔV≈0, т.е. изменение скорости не успевает произойти V = V˚ = const, а при изучении ΔV(t), Δθ(t) можно считать, что быстрое изменение Δα(t), Δωz(t) и Δ 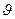 (t) закончилось и принять α, ωz и
(t) закончилось и принять α, ωz и 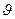 равными балансировочным значениям:
равными балансировочным значениям:
α = αбал, ωz = 0, 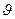 = αбал + θ = const. (β = γa = 0).
= αбал + θ = const. (β = γa = 0).
5.2.1. Собственное продольное короткопериодическое возмущенное движение ВС. Условия устойчивости опорного движения.
Рассмотрим часть уравнений (5.1) для Δθ, Δωz и Δ 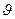 , полагая, что за время быстрого вращательного движения скорость не успевает измениться существенно, т.е. ΔV = 0
, полагая, что за время быстрого вращательного движения скорость не успевает измениться существенно, т.е. ΔV = 0
 = a22 Δθ + a24 Δ
= a22 Δθ + a24 Δ 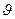 ;
;
 = a32 Δθ + a33Δωz + a34 Δ
= a32 Δθ + a33Δωz + a34 Δ 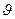 ; (5.6)
; (5.6)
Δ ْ  = Δωz;
= Δωz;
Δθ = Δ 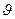 – Δα;
– Δα;
 = Δωz -
= Δωz - 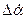 ;
;
Δωz =  +
+ 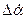 .
.
Из первого:
 =
=  (-
(-  + sinθ) (Δ
+ sinθ) (Δ 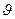 – Δα) +
– Δα) + 
 Δ
Δ 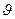 =
=  (sin θ Δθ +
(sin θ Δθ +  Δα).
Δα).
Примем за исходный опорный режим полета – горизонтальный и sin θ = 0. В результате получаем:
 =
= 
 α; (5.7)
α; (5.7)
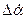 = Δωz –
= Δωz – 
 Δα. (5.8)
Δα. (5.8)
Второе уравнение в системе (5.6) удобнее представить в другой форме (не в форме Коши; см. 3. системы (4.5)).
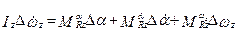 ,
,
или
 , (5.9)
, (5.9)
где
 ;
;  ;
;  ;
; 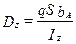 .
.
Дифференцируя (5.8), после подстановки (5.9) и приведения подобных членов, получаем:
 + 2 hk
+ 2 hk 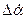 + ωk2
+ ωk2  = 0, (5.10)
= 0, (5.10)
где
 ; (5.11)
; (5.11)
 = -(
= -( +
+ 

 ) = -Dz
) = -Dz  (
( +
+ 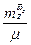 (1+
(1+  )) = -Dz
)) = -Dz 
 ; (5.12)
; (5.12)
nyk = 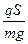 (Сp (α+φp) + Сya);
(Сp (α+φp) + Сya);  =
= 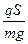 (Сp +
(Сp +  ) =
) =  (1 +
(1 +  );
);  .
.
τ =  (масштаб времени); μ =
(масштаб времени); μ =  (относительная плотность ВС),
(относительная плотность ВС),  ;
;
Нетрудно проверить, что характеристическое уравнение для (5.10) имеет вид:
λ2 + 2hkλ +  = 0. (5.13)
= 0. (5.13)
Условия устойчивости (здесь: a0 =  , a1 = 2hk) c помощью матрицы Гурвица
, a1 = 2hk) c помощью матрицы Гурвица
 : a0 =
: a0 =  >0 и a1 = 2hk>0. Условие
>0 и a1 = 2hk>0. Условие  >0 эквивалентно (см. (5.12)) (при Dz>0,
>0 эквивалентно (см. (5.12)) (при Dz>0,  >0), σn =
>0), σn =  +
+  (1 +
(1 +  )<0 и является критерием асимптотической апериодической устойчивости. Условие 2hk>0 эквивалентно
)<0 и является критерием асимптотической апериодической устойчивости. Условие 2hk>0 эквивалентно  <0;
<0; 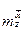 <0;
<0;  >0; Сp>0 и является критерием колебательной асимптотической устойчивости.
>0; Сp>0 и является критерием колебательной асимптотической устойчивости.
Апериодическая неустойчивость возможна при: σn>0, ωk2<0. Колебательная неустойчивость возможна при:  >0, 2hk<0. Соответственно
>0, 2hk<0. Соответственно  = 0 и 2hk = 0 являются условиями граничных значений апериодической и колебательной асимптотической устойчивости по углу атаки в опорном режиме горизонтального полета. При этом асимптотической устойчивости по
= 0 и 2hk = 0 являются условиями граничных значений апериодической и колебательной асимптотической устойчивости по углу атаки в опорном режиме горизонтального полета. При этом асимптотической устойчивости по 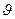 и θ не будет, т.к. с учетом (5.7), (5.6):
и θ не будет, т.к. с учетом (5.7), (5.6):
Δθ(t) = 

 ;
;
Δ 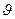 (t) = Δα(t) +
(t) = Δα(t) + 

 ;
;
при Δα(t)→0; Δθ(t)→Δθ0; Δυ(t)→Δθ0, но устойчивость неасимптотическая (по Ляпунову) возможна.
Корни характеристического уравнения:
λ1,2 = -hk±  (5.14)
(5.14)
при  >hk2 и
>hk2 и  >0,будут комплексными сопряженными, а собственное возмущенное движение – колебательное
>0,будут комплексными сопряженными, а собственное возмущенное движение – колебательное
λ1,2 = -hk± i  . (5.15)
. (5.15)
Решение (5.10) имеет вид
Δα = Ae 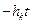 sin (
sin ( + ψ), (5.16)
+ ψ), (5.16)
где hk – коэффициент демпфирования (декремент затухания);
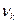 =
=  – круговая частота собственных колебаний (демпфированных колебаний), иногда обозначается ω; ωk – опорная частота или частота недемпфированных колебаний;
– круговая частота собственных колебаний (демпфированных колебаний), иногда обозначается ω; ωk – опорная частота или частота недемпфированных колебаний;
ψ – фазовый угол сдвига. Постоянные А и ψ определяются по заданным начальным условиям: например, при t = t0=0; Δα=Δα0 и 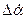 =
= 
Если 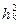 ≥
≥ 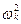 >0, то корни (5.14) будут действительными и собственное возмущенное движение будет апериодическим
>0, то корни (5.14) будут действительными и собственное возмущенное движение будет апериодическим
Δα=c1 eλ1t + c2 eλ2t,
а при 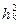 =
= 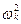 >0; λ1 = λ2 = λ
>0; λ1 = λ2 = λ
Δα(t) = (c1 + c2) eλt.
Постоянные c1 и c2 находятся из начальных условий. Определим теперь Δωz(t). Для этой цели из (5.6) и (5.7) с учетом (5.16), получим
Δωz = 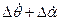 =
= 
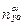 Δα +
Δα + 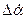 = A
= A  [ (
[ (
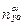 – hk) sin (
– hk) sin ( + ψ) +
+ ψ) + 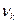 cos (
cos ( + ψ)].
+ ψ)].
5.2.2 Собственное продольное длиннопериодическое возмущенное движение ВС. Условия устойчивости опорного движения
Будем считать, что в конце короткопериодического движения наступает равновесие моментов, mRz ≈ 0 и Δωz и Δ ْ α становятся малыми настолько, что ими можно пренебречь (см. (4.5))
 ;
;
 ; (5.17)
; (5.17)
 ; (Δ ْ ωz = 0).
; (Δ ْ ωz = 0).
(В горизонтальном опорном движении принимаем: Сp = Сxa, nxk ≈ nxa, γa = β = 0, cos θ = 1,  =
=  =
=  ,
,  M ≈ 0);
M ≈ 0);
 ;
;
 =
=  =
= 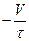
 = g
= g  ;
;
 =
= 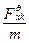 = g(
= g(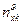 – cos θ) ≈ - g cos θ ≈ -g;
– cos θ) ≈ - g cos θ ≈ -g;
 =
=  ≈
≈  (1 +
(1 + 
 ) =
) =  (
( 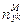 M – nyk + cos θ);
M – nyk + cos θ);
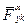 =
=  =
=  (Сp +
(Сp +  ) =
) = 
 =
=  ;
;
 =
=  = Dz
= Dz 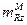
 = Dz
= Dz  (
( +
+ 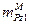 );
);
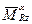 =
=  = Dz
= Dz 
 .
.
Исключая из первого и второго уравнений (5.17) с помощью третьего Δα, получим
 = -2 hд ΔV – g Δθ;
= -2 hд ΔV – g Δθ;
 , (5.18)
, (5.18)
где
 ; (5.19)
; (5.19)
 д2 =
д2 =  (
(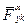
 –
–  ) =
) =  . (5.20)
. (5.20)
Здесь: 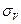 |nya = 1 =
|nya = 1 =  –
– 
Дата добавления: 2015-08-27; просмотров: 54 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аннотация. 6 страница | | | Динамика продольного возмущенного движения ВС 2 страница |