Байес формуласы 5 страница

(1)

(1)-дегі бірінші қосылғыш минималды болады, егер векторы эталонды векторлардың біреуіне жақын болса, ал екінші қосылғыш минималды болады, егер векторының координаттары биполярға жақын болса. Коэффициент 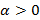осы екі критерийлерді басқарады. функционалын минимизациялау келесі формула бойынша іске асырылады:

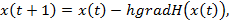
мұндағы итерация номері, градиент қадамы. Градиент векторының координаталарын есептеу үшін олардың дербес туындыларын табамыз:

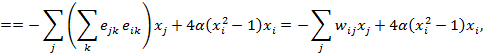
мұндағы эталон номері. Екінші қосылғыш желінің қатысуынсыз ші нейронда есептеледі. ші және ші нейрондар арасындағы байланыс салмағы тең. Сондықтан энергия функционалын минимизациялау келесі формула бойынша іске асырылады:

немесе матрицалық түрде

(2)

мұндағы - вектор координаттарының баған-векторы; -бірлік матрица. Мұндағы , мұндағы -эталонды вектор координаттарының 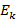вектор бағандарынан құралған матрица. 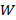матрицасының 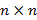өлшемі бар және оның мәні санының модулінен аспайды. Сондықтан және (2) итерационды процесс жинақталады, егер 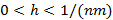. Егер 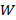матрицасының бас диагоналына нольдік элементтерді қойсақ, итерационды процесс жинақталады.

Хопфилд желісі бірқабатты, толық байланысқан және (1)-суреттегідей құрылымнан тұрады.

Сурет-1

Қабаттағы нейрондардың саны векторлардың санына тең. векторы әрбір нейронның кірісіне беріледі. Бастапқыда синапстың салмақ коэффициенттері теңдей орнатылады:

Хопфилд алгоритмі келесі қадамдардан тұрады:

1) Кіріске сигналы беріледі және деп алынады.

2) Жаңа нейрондардың жағдайы келесі формула бойынша есептеледі

және аксондардың жаңа мәндері келесі формула бойынша есептеледі

3) Аксондардың тұрақтылығы тексеріледі: егер аксондар тұрақталса (яғни ), алгоритм тоқтатылады, кері жағдайда 2- жағдайға қайта ораламыз.

Ескерту. Кейде Хопфилд желісі дұрыс тани алмайды және шығысында болмайтын бейнені шығаруы мүмкін. Бейнені нақты тану үшін саны нен аспауы тиіс, мұндағы вектор өлшемі.

Мысал. Екі 6-өлшемді вектор эталондары берілсін: және . Осы вектор үшін Хопфилд желісін тұрғызу және векторын классифицирлеу керек.

Шешімі. Бейнені танудағы тұрақтылық шарты орындалмайды, себебі үшін синаптикалық байланыс матрицасын құрамыз.

Онда желінің шығысында векторын ұсынғаннан бірінші итерациядан кейін вектор бағанын аламыз, ал белсенділік функциясын қолданғаннан кейін . Сонымен бірінші итерациядан кейін векторын бірінші класқа жататындығын көреміз.

3. Біріктіруші түзу (Соединительная линия)екі объектіні біріктіретін түзу сызықтар салуға қолданылады;

Интерактивті біріктіруші сызықобъектілерге қосылатын және олармен бірге орын ауыстыратын, объектілерді сызықтармен қосуға арналған.

Combine (Соединить) командасы арқылы объектілерді біріктіру

Билет

1.Бейне және класс ұғымы

Бейне –визуалды бейне, көру бейнесі, сурет(кескін)

Бейнелерді тану – түрлі табиғаттағы объектілерді классификациялау әдістері мен алгоритмдері туралы ғылым.

Бейнені тану есебінің көбі интеллектуалды жүйенің негізі болып табылады және келесі бағыттарда:

· символдарды тануда (баспа және жазба мәтіндерінде, банк чектерінде және т.б.);

· әртүрлі жиілік диапазонда (оптикалық, инфрақызыл, дыбыстық, радиожиілікті) алынған бейнелер мен сахнаны талдауда;

· медициналық диагностикада;

· қауіпсіздік жүйелерінде;

· дыбыстарды тануда;

· деректер қорында және білімде (сонымен қатар, Интернет-ресурстарында) іздеу және классификациялауда, кластеризациялауда қолданылады.

Класс (class) — қолдаңылатын қасиеттерінің немесе өңдеу төсілдерінің ортақтылығын сипаттайтын объектілердің жиынтығы.
Класс үлгісі (экземпляр класса; class instance) — кейбір класс конструкторы жасаған нақтылы объектіні белгілейтін объектілік-бейімделген программалау термині.Класс үлгісінің класта анықталған немесе түп кластардан мұралық иемденген объекті мен әдіске тән мәліметтерді сақтайтын қасиеті бар

2. Максимумды арақашықтық алгоритмі.

Максиминдік қашықтық принципіне негізделген алгоритм евклидтік қашықтықты қолданатын тағы да бір эвристикалық әдіс. Бұл алгоритмнің түсіндірілуін келесі мысал түрінде қарастырайық:

Екі өлшемді бейнелерден тұратын он элементті іріктеуге алайық:

10. Объектінің кез келген біреуі, мысалы, – бірінші кластер центрі деп алайық .

11. Осы бейнесінен ең алыс орналасқан элементті тауып, мысалы элементі болсын және бұл элементті екі кластер центрі деп аламыз .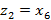

12. Қалған бейнелер мен 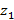және кластер центрлері арасында қашықтық есептелініп, әрбір жұп үшін минималды мән таңдалады.

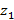X=min (, ), , Y=min(, ),

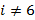
осы екі минималды мәннен үшінші кластердің центрін аламыз:

X₃= max(X,Y)

Егер, соңғы есептелген қашықтық 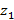және кластерлер центрінен едәуір қашықтықта орналасса, онда -ке сәйкестендірілген бейне оның центрі болып есептеледі.

13. Әрбір үш қашықтық топ арасында минимум мән таңдалады және минимум мәндер ішінде максимум мән элементтердің орта мәнінен үлкен болса, онда ол келесі кластер центрі болады.

14. Нәтижесінде кластер центрлері және { }, { }, { } жиындары анықталады.

3.Photoshop программасында тюнингін жасау

Тюнинг автомобиля (от англ. tuning — настройка, регулировка) — автомобилдің техникалық, динамикалық сапасын жақсарту үщін қолданады. Тюнинг бұл автомобилді жақсартуға ұмтылады. Тюнинг бұл хобби немесе кәсіби қызмет. Көбінесе гонкалық жарысқа қатысушылар қолданады, көбінесе рингтул депте атайды(от англ. ring — кольцо, англ. tool — инструмент).

Стайлинг автомобиля (от англ. styling — стилизация) — салоннан шыққан машинаның сырт түрін жеке адам өз стилімен жасап алуы яғни айналадағы адамдарғың назарын аударатындай кылып жасау. Мысалыға машина басқа түске бояу немесе түрлі-түсті етіп бояу және сол сияқты

Билет

1.Нақты және абстрактылы бейнелер.

Біз кездестіретін көптеген бейнелер екі категорияға бөлеміз: абстрактылы және нақты. Абстрактылы бейнелерге идеялар мен аргументтерді қарастырамыз. Мұндай бейнелерді тану Образы, с которыми мы встречаемся могут быть разбиты на две категории: абстрактные и конкретные. Примером абстрактных образов могут быть идеи и аргументы. Распознавание таких образов относится к концептуальному распознаванию, которое в данном курсе не рассматривается.

Нақты бейнені тануға әріптерді, символдарды, суреттеді, биологиялық кескіндерді, үшөлшемді физикалық объектілерді, сөз сигналдарын, электоркардиограммды, сейсмикалық толқындарды мысал ретінде қарастыра аламыз. Осы бейнелердің кейбіреулері – кеңістікте, қалғандары – уақытша.

Соңғы жиырма жылдық ішінде басты қызығушылық танудағы басты 2 проблемаларға бағытталған болатын:

1) Тірі ағзалармен орындалатын танудың механизмі. Психологтар, физиологтар, биологтар және нейрофизиологтар тірі организмдердің объектілерге қалай қарайтындығын зерттеп білу үшін өздерінің көптеген үлестерін қосқан.

2) Қойылған тапсырманы шешудегі теорияның және тәжірибенің дамуы.

Бұл бағытта инженерлермен қоса қолданбалы математиктер те жұмыс жасауда. Мұнда бейнелерді танудағы барлық тапсырмаларды шешетіндей бірде-бір теория жоқ. Көптеген әдістер мен нақты тапсырмаларды шешудің мысалдары проблемалық бағдарлаудан тұрады.

2.Функция арақашықтығын анықтаудың әдістері. Класс арасындағы арақашықтық.

Жақындық өлшемдері:

· Екі бейнелер арасында

· Бейне және класс арасында

· Екі класс арасында

Өлшем аксиомалары (метрикалық кеңістікте):

1)

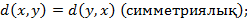
2)

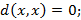
3)

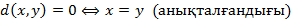
4)

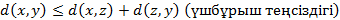
Бұл әдіс 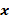бейнесі мен класс арасындағы қашықтықты өлшейтін 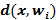функциясын ұсынады. Егер барлық 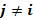үшін 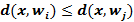болса, онда 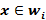деп есептейміз.

Бейне мен класс арасындағы қашықтықты анықтау үшін екі бейне арасындағы қашықтықты анықтау әдісін таңдау керек. Егер бейнелерді метрикалық кеңістіктің элементтері ретінде қарастырсақ, онда қашықтық функциясы ретінде осы кеңістіктің өлшемін алуға болады.

Ол үшін келесі өлшемдерді қолдануға болады:

Дата добавления: 2015-08-26