Интуитивное объяснение

Рассмотрим задачу определения вероятности того, что некоторая точка в N-мерном евклидовом пространстве принадлежит множеству, которое задано набором точек, определённо принадлежащих данному множеству. Найдем центр масс множества. Интуитивно понятно, что чем ближе заданная точка к центру масс, тем больше вероятность того, что она принадлежит множеству.

Однако также стоит учитывать, на какого размера области рассредоточены точки множества, чтобы понять, насколько значимо расстояние между заданной точкой и центром масс. Самый простой подход заключается в вычислении среднеквадратичного отклонения точек множества от центра масс. Если расстояние между заданной точкой и центром масс меньше среднеквадратичного отклонения, то можно заключить, что вероятность принадлежности точки множеству высока. Чем дальше точка, тем больше вероятность того, что она не принадлежит множеству.

Этот интуитивный подход можно определить математически через расстояние между заданной точкой и множеством по формуле 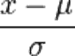. С помощью подстановки этого значения в нормальное распределение можно найти вероятность принадлежности точки множеству.

Недостаток такого подхода заключается в использовании предположения о том, что точки множества сферически распределены вокруг центра масс (то есть равномерно по всем измерениям). Если же распределение явно не сферическое (например, эллипсоидальное), то было бы естественным учитывать в вероятности принадлежности не только расстояние до центра масс, но и направление на него. В направлении короткой оси эллипсоида заданная точка должна быть ближе к центру масс, чтобы принадлежать множеству, в то время как в направлении длинной оси она может быть дальше.

Для записи этого в математическом виде эллипсоид, лучшим образом представляющий вероятностное распределение множества, может быть задан матрицей ковариаций множества. Расстояние Махаланобиса — это просто расстояние между заданной точкой и центром масс, делённое на ширину эллипсоида в направлении заданной точки.

2. Белгілер векторлары арасындағы қашықтықты есептеу әдісі

Векторлар арасындағы өлшенетін қашықтықтың әртүрлі өлшемі, белгілердің басымдылықтары болуы мүмкін. Сондықтан салмақтық өлшемдер қарастырылады. Мысалы, Минковский салмақтық өлшемі келесі түрде болады:

,

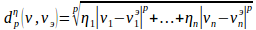мұндағы оң салмақ векторы 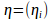белгілердің басымдылықтары мен шамасы жөнінде ақпаратпен анықталады. Егер мұндай ақпарат векторды анықтау үшін аз болса, онда өлшенетін шамаларды нормалайтын, мысалы Канберра өлшемін қолданамыз:

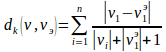
3. Фрактальды графика

Фракталды кескіндер - қазіргі таңда қарқындап дамып келе жатқан кескіндердің бірі болып
табылады. Фрактал, фракталды геометрия және фракталды графика түсінігі, 70 - шы жылдардың
аяғынан бастап, бүгінге дейінгі математика ғылымы мен компьютерлік суретшілердің кең
қолданысына ие. Фрактал сөзі латынның «fractus» «фрагменттерден тұратын» деген мағынаны
береді.

Фрактальда графиканың информатика ғылымынды кең өріс алған мысалға Компьютерлік
ойындардарда бегілі бір табиғаттағы объектінің үлгісін алу үшін (теңіз беттері, өсімдіктердің,
бұлттардың). Келесі бағыты фрактальды өз сапасын жоғалтпайтын сығылған суреттер (10-нан
2000-ға дейін сығылған) алу үшін.
Фрактальды графика негізінен кластарға жіктеледі:
Геометриялық
Алгебралық
Стохастикалық

Геометриялық фракталдар. Бұндай фракталдардың тарихы 19 ғасырда математиктердің
зерттеуі бойынша басталды. Бұл класқа жататын фрактал өзіндік бөлік анық көрінеді.
Мысалға геометриялық фракталдарға мыналар жатады:
Серпинстік ұшбұрыш,триадндық қисық Кох,қисық Пеано т.б
Геометриялық фракталдар қарапайым жолме құрылады
1. Бастапқы шарт қойылады: фракталға байланысты құрылатын фигура
2. Байланыс орнатылады
3. Нәтижеде бұл байланыстың қайталануы арқасында геометриялық фрактал пайда болады

Билет

Сурак

Бейнелерді тану пәні. Бейнелерді тану – түрлі табиғаттағы объектілерді классификациялау әдістері мен алгоритмдері туралы ғылым.

Бейнені тану есебінің көбі интеллектуалды жүйенің негізі болып табылады және келесі бағыттарда:

· символдарды тануда (баспа және жазба мәтіндерінде, банк чектерінде және т.б.);

· әртүрлі жиілік диапазонда (оптикалық, инфрақызыл, дыбыстық, радиожиілікті) алынған бейнелер мен сахнаны талдауда;

· медициналық диагностикада;

· қауіпсіздік жүйелерінде;

· дыбыстарды тануда;

· деректер қорында және білімде (сонымен қатар, Интернет-ресурстарында) іздеу және классификациялауда, кластеризациялауда қолданылады.

· Бейнелерді тану теориясының негізгі есептері. Сандарды, әріптерді және т.б. символдарды тануды іске асыратын техникалық жүйе мысалында бейнелерді тану теориясының негізгі есептерін қарастырайық. Мұндай жүйе 60-жылдары АҚШ-да жасалған және ұзақ уақыт бойы конвертті символдарды тану үшін қолданылған.

Мысалы, тану жүйесінің кірісіне қағаз лентада жазылған қандай да бір х символы келіп түссін және осы символды тану керек болсын. Тану керек объектілерді бейне («pattern») деп атайды. Солдан оңға қарай жылжитын есептеуші басы бар техникалық жүйе уақытына тәуелді боялған бет ауданының өзгерісін жылдамдығы өлшейді (1.1-сурет). символ-бейнесінің функциясы оның бейнеленуі болып табылады. Сигналды уақыттың дискретті нүктелерінде өлшесек, х символын х векторы түрінде аламыз. функциясын функциялар кеңістігінде элемент-вектор деп есептей аламыз. Бір түрден екінші түрге ауысу, ереже бойынша, бейне туралы ақпараттар санын азайтады.

Сурет 1.1

Кіріс х символ-бейнесі кластар жиынының қандай да бір класына жатуы мүмкін - әрбір класс қандай да бір символға (әріпке, санға және т.б.) сәйкес келеді. Кластарды бір-бірімен қиылыспайды деп аламыз.

>

Оқыту

Белгілерді таңдау

Классификатор

Бейнені векторлық форма түрлендіру

Сурет 1.2 Бейнелерді тану жүйесінің жалпы сызбасы

Бейнелерді тану есебі х бейнесінің 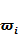кластарының біріне жатқызу болып табылады. Бейнені бір класқа жатқызу ережесін классификатор деп атап, классификация бөлімінде іске асырылады. Егер бейне метрикалық кеңістіктің элемент-векторы болса, бейнені класқа жатқызуды, мысалы, вектор мен класс арасындағы қашықтықты есептеу көмегімен іске асыра аламыз. Классификатор шығысында кіріс бейнесінің қай класқа (класс номерін) жататындығын немесе ешқандай класқа жатпайтындығын анықтауымыз қажет.

Бейненің векторлық формаға түрлендіру бөлімімен классификатор арасында кішкене санды таңдау бөлімі (мысалы, аналогты сигналының х векторына түрленуі) болуы мүмкін. Мұндай бөлімнің болуы вектор өлшемін азайтып, тану жүйесінің жылдамдығын арттырады.

Жалпы, тану жүйесінде оқыту бөлімі болуы мүмкін. Бұл бөлім оқытылатын бейнелерді таңдау кезінде классификация ережесін қалыптастыруға мүмкіндік береді. Сонымен қатар, оқытылатын бейнелер бойынша ақпараттық белгілерді таңдау ережесі қалыптасады.

Сурак

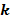-ішкі топтық орташа алгоритмі

Бұл алгоритм 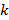ішкі топтық орташа есептеулерге негізделіп, келесі қадамдардан тұрады:

1. 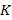кластер центрлері 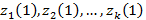таңдалынады. Мұндай іріктеу қалауымызша алынады және алғашқы 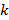берілгендер элемент жиындарын іріктеу қолданылады.

2. Итерацияның 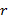-ші қадамында берілген {x} бейнелер жиыны 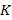кластерлерге келесі ережелер бойынша бөлінеді.

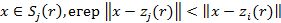(1)

мұндағы, 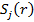- центрлері 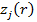болатын кластерлерге кіретін бейнелер жиыны.

(1)-формуланың теңдік жағдайында шешім қалауымызша орындалады.

3. 2-қадамның нәтижесі арқылы 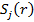- жиынына жататын барлық бейнелер арасындағы арақашықтық қосындысының квадратына тең және жаңа кластер центрі минималды болуы шартынан жаңа кластер центрлері 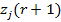, j=1,2…k анықталады. Басқаша айтқанда, жаңа кластер центрлері 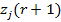келесі сапа көрсеткішін минимизациялау бойынша таңдалуы керек:

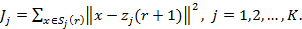(2)

Бұл формула 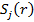жиынында анықталған 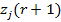центрі сапа көрсеткішінің ең кішісін қамтамасыз етеді, яғни кластер центрлері мына формуламен анықталады.

Жаңа кластер центрлері келесі формуламен анықталады:

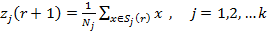(3)

мұндағы 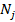- 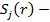ге кіретін таңдалатын бейнелердің саны

4. 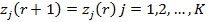теңдігі шарты орындалса, онда бұл алгоритмнің жинақталу шарты болып табылады және осындай нәтижеге жету алгоритмнің жалғастыруын тоқтатады, кері жағдайда екінші қадам қайта есептеледі. Сонымен алгоритм бітеді.

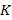ішкі топтық орта есептеу негізінде алгоритм жұмысының сапасы кластер центрлерін таңдау санына, кластер центрлерін таңдауына, бейнелерді қарастыру тізбегіне және бейнелердің геометриялық ерекшеліктеріне байланысты.

Мысалы:

1 қадам. 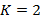деп берілсін және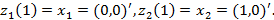

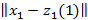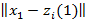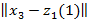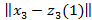
2қадам. < және [[ ]]< 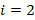болғандықтан, онда S₁ жиынын S₁(1)={x₁,x₃}деп аламыз. Сол сияқты басқа бейнелер 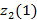кластер центріне жақын екені анықталсын, сондықтан S₂(1)={x₂, x₄, x₅,…x₂₀}.

3 қадам. Кластер центрлерін түзету мәндері

Z₁(2)= =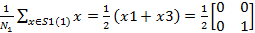

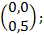
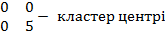
Z₂(2)=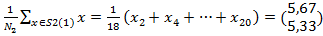

4 қадам. 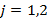болғанда Z_j(2)≠Z_j(1) болғандықтан 2-қадамға қайта ораламыз.

2 қадам. Жаңа кластерлер центрлерін таңдау мынадай теңсіздікке әкеледі.

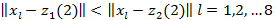үшін, және 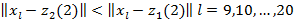үшін. Бұдан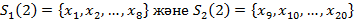

3 қадам. Кластер центрлерін түзету мәндері

=

=

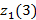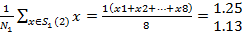
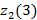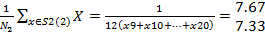
4 қадам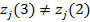_. болғандықтан 2-қадамға қайта ораламыз.

2 қадам. Алғашқы итерацияда есептелінген мәндерді аламыз.

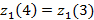
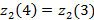
3 қадам. Соған сәйкес 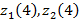элементтері тағы да алынады.

4 қадам. 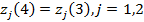болғандықтан, алгоритм орындалды, нәтижесінде келесі кластер центрлері алынды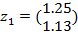

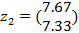
Сурак

Трёхмерная графика (3D (от англ. 3 Dimensions — «3 измерения») Graphics, Три измерения изображения) — разделкомпьютерной графики, совокупности приемов и инструментов (как программных, так и аппаратных), предназначенных для изображения объёмных объектов.

Трёхмерное изображение на плоскости отличается от двумерного тем, что включает построение геометрической проекции трёхмерной модели сцены на плоскость (например, экран компьютера) с помощью специализированных программ (однако, с созданием и внедрением 3D-дисплеев и 3D-принтеров, трёхмерная графика не обязательно включает в себя проецирование на плоскость). При этом модель может как соответствовать объектам из реального мира (автомобили, здания, ураган, астероид), так и быть полностью абстрактной (проекция четырёхмерногофрактала).

3D-моделирование — это процесс создания трехмерной модели объекта. Задача 3D-моделирования — разработать визуальный объемный образ желаемого объекта. С помощью трехмерной графики можно и создать точную копию конкретного предмета, и разработать новое, даже нереальное представление до сего момента не существовавшего объекта.

Трёхмерная графика активно применяется для создания изображений на плоскости экрана или листа печатной продукции в науке и промышленности, например всистемах автоматизации проектных работ (САПР; для создания твердотельных элементов: зданий, деталей машин, механизмов), архитектурной визуализации (сюда относится и так называемая «виртуальная археология»), в современных системах медицинской визуализации.

Самое широкое применение — во многих современных компьютерных играх, а также как элемент кинематографа, телевидения, печатной продукции.

Трёхмерная графика обычно имеет дело с виртуальным, воображаемым трёхмерным пространством, которое отображается на плоской, двухмерной поверхности дисплея или листа бумаги. В настоящее время известно несколько способов отображения трехмерной информации в объемном виде, хотя большинство из них представляет объёмные характеристики весьма условно, поскольку работают со стереоизображением. Из этой области можно отметить стереоочки, виртуальные шлемы, 3D-дисплеи, способные демонстрировать трехмерное изображение.

Билет

1. Роль и место распознавания образов в автоматизации управления сложными системами

Дата добавления: 2015-08-26