Байес формуласы 2 страница

Сурет 3.2 Үш класс арасындағы қашықтық

Жалпы жағдайда қашықтық функциясы көмегімен барлық белгілер кеңістігін ондағы белгілі 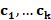класс центрлеріменкез келген 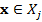нүктесі және барлық үшін болатындай етіп жеке облыстарына бөлеміз. Мұндай облыстарды Воронов клеткалары, ал барлық Воронов клеткаларының жиынын – Воронов диаграммасы деп атайды. Евклид кеңістігінде Воронов клеткаларының шекарасы барлық жағдайда қандай да бір көпжақтылар болып табылады (3.3-сурет).

Сурет 3.3 Воронов клеткалары

Екінші әдіс - жақын көршілер әдісі. Бұл әдісте қашықтықты есептеу келесі қадамдардан тұрады:

a. элементін анықтаймыз, яғни

.

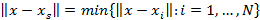b. шарт тексеріледі: егер болса, онда жатады деп есептеледі. Бұл жағдайда қашықтық функциясы келесі формуламен анықталады

.

Бұл әдіс дұрыс емес классификациялау нәтижесінде қателікті жіберу мүмкіндігі жоғары, сондықтан берілгендердегі қателік аз болған жағдайда қолданылады.

Егер облысында қиылыспайтын облыстары бар болса, онда белгілер кеңістігін болатындай жеке облыстарға бөлеміз. Мұндай облыстарды Воронов облыстары (немесе Дирихле облыстары) деп атайды.

Үшінші әдіс - эталондық бейнеге дейінгі қашықтықты анықтау. Бұл әдіс бір эталонды бейне – класс центрімен анықтау қиын болған жағдайда қолданылады және эталон бейнесін енгізу мен кластың құрылымдық немесе геометриялық қасиеттерін білуге негізделген. Мұндай жағдайдың белгісі болып класс элементтері дисперсиясының үлкен мәні болып саналады. Сонымен қатар таңдалатын оқытудағы кейбір элементтер жиыны ерекшеленеді (эталондық бейнелер деп аталатын). Мұндай біртекті құрылымдар бір эталонды бейненің шеңберінде жинақталады және ол кластер деп аталады.

Егер эталондық бейнелер белгілі болып, класс элементтері бірнеше эталондық бейнелерді айналдыра жақсы топтастырылса, онда берілген және класы арасындағы қашықтық келесі формула бойынша анықталады:

мұндағы - класының эталондық бейне-векторы.

Кластың эталондық бейнелерін табу есебі осы класта қайталанатын құрылымды ерекшелеумен және олардың центрін табумен шешіледі. Қайталанатын құрылымдар нақты қайталану критерийлерін қанағаттандыратын векторлар жиынын ұсынады. Мұндай құрылымдарды кластерлер, ал құрылымды табу есебін – кластеризация есебі деп атайды. Оқыту таңдауын кластерге бөлу есебін кластеризация деп атаймыз.

Ескерту. Кейбір есептерде және кластар арасындағы қашықтығын есептеу керек. Бұл қашықтықты мақсатына, кластар құрылымына және дұрыс емес шешу құнына байланысты түрлі жолдармен анықтауға болады. Кластар арасындағы қашықтықты келесі әдістермен есептеуге болады:

1. екі элемент арасындағы минималды қашықтық, әр элемент сәйкесінше өз класына жатады;

2. барлық элементтер жұбы арасында орташа қашықтықты табу, әр элемент өз класына жатады, мұндағы кластар арасындағы барлық элемент жұптарының жиыны;

3. элемент жұптары арасындағы максималды қашықтық, әр элемент өз класына жатады;

4. кластары арасындағы қашықтық, мұндағы кластырының сәйкесінше центрлері.

Воронов диаграммасын тұрғызатын мысалды қарастырайық.

Воронов диаграммасы S көп нүктелі жазықтығын бөліктерге бөлуге негізделген, әрбір бөліктегі нүктелер жиынтығы S көпмүшісінің элементтеріне барынша жақын орналасуы керек.

3. Растрлық бейнелерді құратын бағдарламалық құралдарға шолу.

1.2 Растрлық графика - көптеген ұсақ бөлінбейтін нүктелерден(пиксельдерден) тұратын тікбұрышты матрица.

Растрлық бейнелерді өңдеу

Растрлық бейнелерді қою үшін Файл – Импорт командасы пайдаланылады. Сонда орнату шартын анықтауға болады (алғашқы бейненің тек бөлігін ғана қою немесе қою кезінде алғашқы өлшемін өзгерту), бірақ сол операцияларды бейнені қойғаннан кейін де орындауға болады.

Бейненің өлшемін өзгерту Таңдау (Выбор) құралы немесе Точечный рисунок – Изменить размер командасын таңдау арқылы жүзеге асыруға болады. Сонымен қатар көрсетілген команда көмегімен қажет нәтижеге байланысты растрлық бейне түрін өзгертуге болады.

Форма құралы бейнені дербес формада алуға мүмкіндік береді. Сонда қисықтың тораптық нүктелерін қосуға немесе жоюға болады.

Пышақ құралы көмегімен дербес қисық бойынша бейнені қиюға болады.

Резинка құралы бейненің бөлігін жоюға мүмкіндік береді, сонда бүтін фрагменттерді Arrange -> Break RGB Bitmap Apart командасы көмегімен бір-бірінен алыстатуға болады.

Билет

1. Кластерді шығару қарапайым алгоритмі.

Кластерлеу алгоритмдері

Векторлық кванттаудың идеясы – белгілер кеңістігін кластер нүктелері шешіліп жатқан тану есебі үшін бірдей болатындай қиылыспайтын кластер-облыстарына бөлу болып табылады. Кластер сандары кластар санынан ереже бойынша көп болып саналады.

Кластарды кластерлерге бөлу – бұл оқытылатын 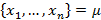таңдаулардан және барлық үшін шарттары орындалса, ішкі жиынын бөліп алуды айтамыз.

Кез келген кластердің эталонды бейнесі оның центрі болады:

Кластер центрі айналасында жатқан элементтердің шашылу шамасы (кластер дисперсиясы) келесі формуламен есептеледі:

мұндағы - ші кластердегі элементтер саны.

Егер функционалы минималды болса, элементтер жиынын кластерлерге бөлу сәтті аяқталды деп есептеуге болады.

1-әдіс. Кластер центрлерін қоюдың қарапайым әдісі. {x₁, x₂, …. х_n} бейнелерінің N жиыны (бейнелер берілісі) берілсін.

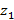- бірінші кластердің центрі деп алынып, кез-келген берілген бейнелердің біреуімен сәйкестендірілсін және кез келген теріс емес, шекті шама Т анықталсын.

Есептеуге ыңғайлы болу үшін бірінші кластердің центрін деп алайық. Осыдан кейін бейнесі 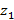кластердің центрі аралығындағы қашықтық 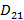есептелінеді. Егер осы қашықтық Т шекті шамадан үлкен болса, онда жаңа кластер 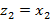центрі анықталады деуге болады, басқаша жағдайда бейнесінің центрі болатын кластерге жатады.

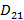> Т шарты орындалады деп, жаңа центр кластері болсын. Келесі қадамда бейнесінен 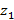және кластер центрлері арасындағы қашықтық есептелініп, сәйкесінше және деп аламыз. Егер екі қашықтық Т шекті шамадан үлкен болса, онда кластер центрі, кері жағдайда x₃ 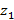және кластердің қайсысына жақын соған жатқызылады. Тағы да сол сияқты жаңа бейне мен белгілі кластер центрі арасындағы қашықтық есептелініп, Т шекті шамамен салыстырылады.

Мұндай алгоритмнің өте көп кемшілігі болғанымен, орындалуы қарапайым және берілгендер жиыны түрінде негізгі сипаттаманы өте жылдам ұсынады.

2-әдіс. Максиминдік қашықтық алгоритмі.

Максиминдік қашықтық принципіне негізделген алгоритм евклидтік қашықтықты қолданатын тағы да бір эвристикалық әдіс. Бұл алгоритмнің түсіндірілуін келесі мысал түрінде қарастырайық:

Екі өлшемді бейнелерден тұратын он элементті іріктеуге алайық:

1. Объектінің кез келген біреуі, мысалы, – бірінші кластер центрі деп алайық .

2. Осы бейнесінен ең алыс орналасқан элементті тауып, мысалы элементі болсын және бұл элементті екі кластер центрі деп аламыз .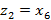

3. Қалған бейнелер мен 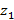және кластер центрлері арасында қашықтық есептелініп, әрбір жұп үшін минималды мән таңдалады.

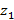X=min (, ), , Y=min(, ),

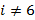
осы екі минималды мәннен үшінші кластердің центрін аламыз:

X₃= max(X,Y)

Егер, соңғы есептелген қашықтық 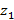және кластерлер центрінен едәуір қашықтықта орналасса, онда -ке сәйкестендірілген бейне оның центрі болып есептеледі.

4. Әрбір үш қашықтық топ арасында минимум мән таңдалады және минимум мәндер ішінде максимум мән элементтердің орта мәнінен үлкен болса, онда ол келесі кластер центрі болады.

5. Нәтижесінде кластер центрлері және { }, { }, { } жиындары анықталады.

3-әдіс. 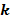-ішкі топтық орташа алгоритмі

Бұл алгоритм 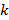ішкі топтық орташа есептеулерге негізделіп, келесі қадамдардан тұрады:

1. 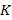кластер центрлері 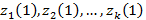таңдалынады. Мұндай іріктеу қалауымызша алынады және алғашқы 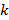берілгендер элемент жиындарын іріктеу қолданылады.

2. Итерацияның 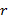-ші қадамында берілген {x} бейнелер жиыны 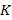кластерлерге келесі ережелер бойынша бөлінеді.

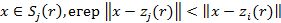(1)

мұндағы, 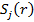- центрлері 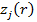болатын кластерлерге кіретін бейнелер жиыны.

(1)-формуланың теңдік жағдайында шешім қалауымызша орындалады.

3. 2-қадамның нәтижесі арқылы 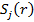- жиынына жататын барлық бейнелер арасындағы арақашықтық қосындысының квадратына тең және жаңа кластер центрі минималды болуы шартынан жаңа кластер центрлері 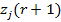, j=1,2…k анықталады. Басқаша айтқанда, жаңа кластер центрлері 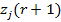келесі сапа көрсеткішін минимизациялау бойынша таңдалуы керек:

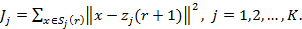(2)

Бұл формула 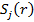жиынында анықталған 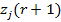центрі сапа көрсеткішінің ең кішісін қамтамасыз етеді, яғни кластер центрлері мына формуламен анықталады.

Жаңа кластер центрлері келесі формуламен анықталады:

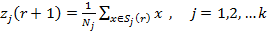(3)

мұндағы 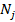- 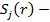ге кіретін таңдалатын бейнелердің саны

4. 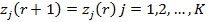теңдігі шарты орындалса, онда бұл алгоритмнің жинақталу шарты болып табылады және осындай нәтижеге жету алгоритмнің жалғастыруын тоқтатады, кері жағдайда екінші қадам қайта есептеледі. Сонымен алгоритм бітеді.

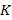ішкі топтық орта есептеу негізінде алгоритм жұмысының сапасы кластер центрлерін таңдау санына, кластер центрлерін таңдауына, бейнелерді қарастыру тізбегіне және бейнелердің геометриялық ерекшеліктеріне байланысты.

2. ISODATA алгоритмі: ISODATA классификация әдісі (мәлімет анализінің өздігінен ұйымдастырылатын итерациондық әдісі- Iterative Self-Organizing Data Analysis Technique).

ISODATA – бұл, кластерлік анализге негізделген процесс. Бір классқа түстерінің ашықтық мәні бойынша спектралды белгілері жақын кеңістіке жататын пикселдер жатады. ISODATA кластеризация алгоритмі белгілі бір қасиеттермен байланысқан бейне жиынын ішкі жиындарға бөліп жұмыс істеуге негіделген.

ISODATA алгоритмі әр бір пиксель үшін сәйкесінше кластерді анықтау үшін минималды спектралды арақашықтықты қолданады. Кластердің кездейсоқ ортақ мәнін тағайындау процессінен басталады және бұл процесс шығу мәліметтерінің әр бір кластерлерінің ортақ мәні тағайындалған мәнге жеткенше қайталана береді. Класстерлердің бастапқы ортақ мәндері спектралды кеңістіктің орталық векторының бойымен үйлестіріледі.

3. ФОТОМОНТАЖ (фото... және монтаж) — фотография бейне жасау мақсатымен фотосуреттердің белгілі бір ортақ тақырыпқа топтастырылып берілуі. Фотомонтаж плакаттар, жарнамалар, фотоәзілдер дайындауда кеңінен қолданылады. Кейде Фотомонтажда график. материалдар да пайдаланылады. Фотомонтаж мех. және проекц. тәсілдермен жасалынады. Бірінші жағдайда фотосуреттерден қажетті бейнелерді (немесе бөліктерді) ойып, немесе қырқып алады да, оларды қалың қағаздың бетіне желімдейді; араларына ретушь жасап, фотоға қайта түсіреді. Екінші тәсіл бойынша, фотоқағаздан бетіне фотоүлкейткіштің көмегімен негативтен қажетті бейнелердің проекциясы ретімен түсіріп алынады.

Билет

1.Минималды кеңістікте белгілерді анықтау.

Минималды кеңістікте белгілерді анықтау конверттегі цифрларды тану мысалында:

а)0,1,2,3 (белгілердің бірөлшемді кеңістігі, белгілер – көлденең не тік сызықтардың саны);

б) 0, 1, …, 8 (белгілардің екіөлшемді кеңістігінде, белгілер – горизонтальды және вертикальды сызықтырдың саны)

в)барлық цифр (белгілердің үшөлшемді кеңістігі, белгілер - – горизонтальды және вертикальды сызықтырдың саны, және жоғарғы және төменгі сызықтар санында,ы айырмашылық)

г)барлық цифр (тоғызөлшемді кеңістік, белгілер – қолдағының логикалық сипаттамасы немесе 9 орынның біреуінде сызықтың болмауы)

2. Екіөлшемді кеңістікте белгілердің графикалық берілудің мысалдарын қарастыру(мысалы, 1б пункті конверттегі цифрды тану)

3. Бейнелердің класын белгілеу және оларды сызықты фцнкцияларға бөлу (кластардың сызықты бөлінуін жеке қарастыру). Мысалы,сызықты функция көмегімен конверттегі цифрлардың екі класқа: жай және күрделі сандар бөлінуін қарастыру

2. Шындыққа жақын функция.

Екінші ретті 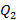ықтималдылық қатесі минималды болады, егер

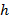болса, мұндағы шекті шамасы келесі қатынастардан анықталады:

Шешімдерді қабылдау теориясында функциясы шындық функция, ал – шындық қатынасы функциясы деп аталады.

Коллаж

Коллаж -әр түрлі фотосуреттерді біріктіріп, қажетті мазмұндағы әсерлі сурет жасау тәсілі.

Фотоколлаж — соединение нескольких фотоизображений в одной картинке, при котором все объекты смотрятся как единое целое.

Коллаж жасау үшін қажет форматтағы фон, коллаж жасалынатын суреттер

Adobe Photoshop (версия от CS3 и выше) программасы керек.

1.Жаңа фон құру («Файл» — «Создать…» Ctrl+N),Фон кез-келген түсте болады.

2.Керек фотоларды ашу(«Файл» — «Открыть…»)

3.Бірінші ашылған суретке өтіңіз және суретті «Тікбұрыш облысы».(Сонымен қатар, толық суретті белгілей аламыз: «Белгілеу-толық» Ctrl+A)

4. Суретті көшіру ((«Редактировать» — «Копировать» либо Ctrl+C)

5. Коллаж фоны бар қосымша бетті табыңыз

6.Суреттіорналастырыңыз, «Редактировать» — «Вставить» немесе Ctrl+C. Сурет фонда орналасады және қабатта жаңа қабат пайда болады.

7.Суретті қажет мөлшерде өзгерту үшін «Редактирование» -«Масштабирование->Трансформирование» және суретті қажет жерге апарыңыз(және фото өлшемін үлкейте кішірейте аласыз).

8. «Редактирование» — «Трансформирование» бетінде «Поворот» функциясы орналасқан, суретті пударуға болады,

9.Дәл осы қадамдарды қалған суреттерге орындап шығыңыз. Келесі ретте «Слои» бөліміне өтіңіз, және тышқанның оң жақ батырмасын басып «Объединить видимые» пунктін таңдаңыз. Осы түрде сіздің коллажыңыз бір толық сурет болады.

10.Дайын коллажды сақтау.

Билет

1. Бейнені танудың логикалық әдістері.

Логикалық түрде сипатталуы – бұл ақиқат немесе жалған болатын сөйлем болып табылады.

Логикалық әдісте математикалық логиканы қолдану проблемасымен, бейнені танудың әдістеріндегі қисықтарды идентификациялау үшін қолданылады. Бұл әдіс логикалық белгімен объектілердің күйі арасында құрылады,сондықтан тек қарапайым екі мағына қабылдай алатын (0 және 1) белгілерін қолданады. Жүйенің күйі (ия-жоқ, ақиқат – жалған, 0 – 1) символдарымен белгіленеді. Екі мәнді қабылдайтын ауыспалы көлеммен функцияны логикалық деп аталады.

Логикалық көлем дегеніміз бір ғана мәнді қабылдайтын(0–1) көлем.Логикалық көлем- бас латын әріптері. Екі логикалық А және В ауыспалының логикалық суммасы логикалық С (дизъюнкция). ауыспалы болып табылады. С колемі ақиқат болады (С = 1), егер А және В пікірінің біреуі ақиқат болса:

(29)

Екі А және В көлемнің логикалық туындысы С көлемі болып табылады (конъюнкция).

2.Классификацияның минимаксты критерийі

Статистикалық көзқарас бойынша байестік классификация ең жақсы классификация болып саналады. Бірақ барлық кезде бұл әдісті қолдана алмаймыз. Мысалы, ықтималдылығы белгісіз жағдайда қолдану мүмкін емес.

Дата добавления: 2015-08-26